764. 最大加号标志
在一个 n x n 的矩阵 grid 中,除了在数组 mines 中给出的元素为 0,其他每个元素都为 1。mines[i] = [xi, yi]表示 grid[xi][yi] == 0
返回 grid 中包含 1 的最大的 轴对齐 加号标志的阶数 。如果未找到加号标志,则返回 0 。
一个 k 阶由 1 组成的 “轴对称”加号标志 具有中心网格 grid[r][c] == 1 ,以及4个从中心向上、向下、向左、向右延伸,长度为 k-1,由 1 组成的臂。注意,只有加号标志的所有网格要求为 1 ,别的网格可能为 0 也可能为 1 。
示例 1:
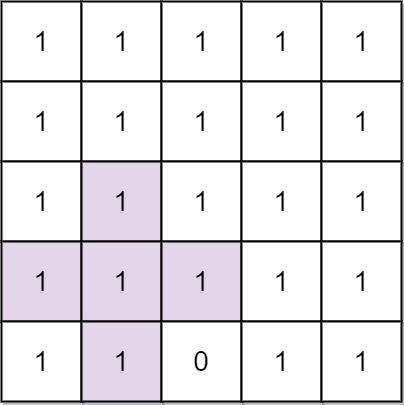
输入: n = 5, mines = [[4, 2]] 输出: 2 解释: 在上面的网格中,最大加号标志的阶只能是2。一个标志已在图中标出。
示例 2:

输入: n = 1, mines = [[0, 0]] 输出: 0 解释: 没有加号标志,返回 0 。
-------------------------------------------------------------------------------------------------------
leetcode官方给出的动态规划解法,理解之后自己敲出来

1 class Solution {
2 public int orderOfLargestPlusSign(int n, int[][] mines) {
3 int[][] dp = new int[n][n];//用于存放每个位置的加号标志的阶数
4 for(int i = 0; i < n; i++){//先给每一个位置默认为最大阶
5 Arrays.fill(dp[i],n);
6 }
7
8 Set<Integer> mine = new HashSet<Integer>();
9 for(int[] num : mines){//将所有为0的位置记录下来
10 mine.add(num[0]*n + num[1]);
11 }
12
13 int count = 0;
14 for(int i = 0; i < n; i++){
15 //left
16 int res = 0;
17 for(int j = 0; j < n; j++){
18 if(mine.contains(i*n + j)){
19 res = 0;
20 }else {
21 res++;
22 }
23 dp[i][j] = Math.min(dp[i][j], res);
24 }
25 //right
26 res = 0;
27 for(int j = n-1; j >= 0; j--){
28 if(mine.contains(i*n + j)){
29 res = 0;
30 }else {
31 res++;
32 }
33 dp[i][j] = Math.min(dp[i][j], res);
34 }
35 }
36 for(int i = 0; i < n; i++){
37 //up
38 int res = 0;
39 for(int j = 0; j < n; j++){
40 if(mine.contains(j*n + i)){
41 res = 0;
42 }else {
43 res++;
44 }
45 dp[j][i] = Math.min(dp[j][i], res);
46 }
47 //down
48 res = 0;
49 for(int j = n-1; j >= 0; j--){
50 if(mine.contains(j*n + i)){
51 res = 0;
52 }else {
53 res++;
54 }
55 dp[j][i] = Math.min(dp[j][i], res);
56 count = Math.max(dp[j][i], count);
57 }
58 }
59 return count;
60 }
61 }
标签:int,res,mines,++,加号,119,dp From: https://www.cnblogs.com/wzxxhlyl/p/16873363.html