20230406 9.2. 希尔排序（ by Donald Shell ）

希尔排序（ by Donald Shell ）

• 定义增量序列 \(D_M > D_{M-1} > … > D_1 = 1\)
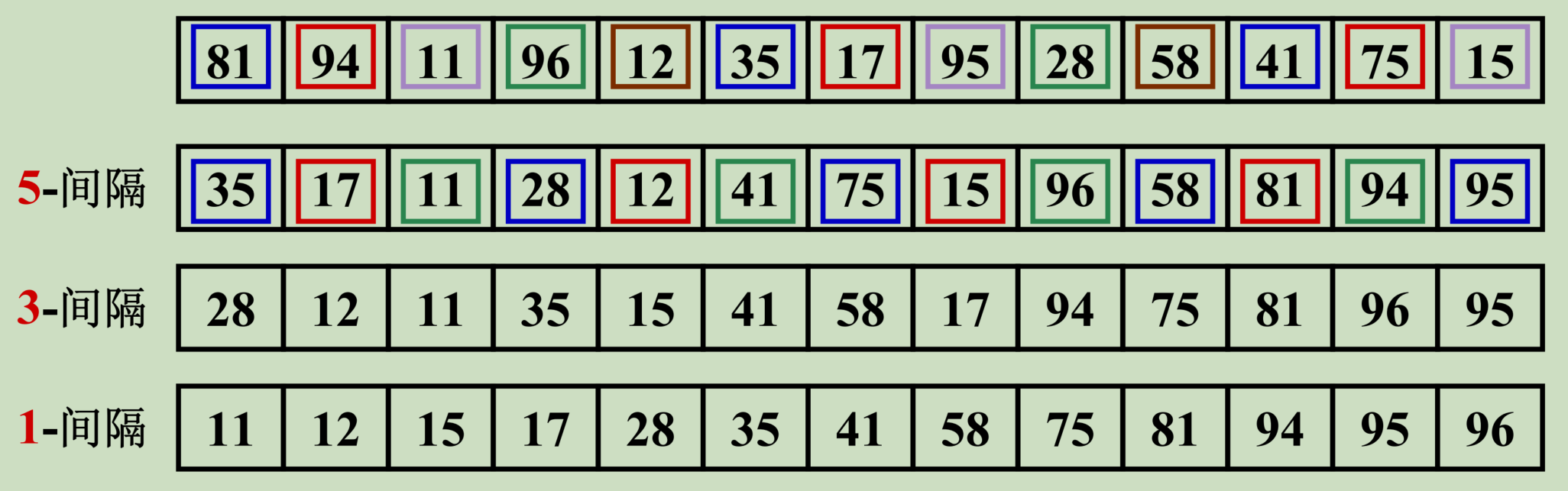
• 对每个 \(D_k\) 进行 \(D_k-间隔\) 排序( k = M, M-1, … 1 )
• 注意： \(D_k-间隔\) 有序的序列，在执行 \(D_{k-1}-间隔\) 排序后，仍然是 \(D_k-间隔\) 有序的

希尔增量序列

原始希尔排序 $D_M = N / 2 $ , $D_k = D_{k+1} / 2 $

void Shell_sort( ElementType A[], int N ) 
{ 
    for ( D=N/2; D>0; D/=2 ) { /* 希尔增量序列 */
        for ( P=D; P<N; P++ ) { /* 插入排序 */
            Tmp = A[P]; 
            for ( i=P; i>=D && A[i-D]>Tmp; i-=D ) {
                A[i] = A[i-D]; 
            }
            A[i] = Tmp; 
        }
    }
}

• 最坏情况： \(T = Θ( N2 )\)
• 举个坏例子：增量元素不互质，则小增量可能根本不起作用

更多增量序列

• Hibbard 增量序列
  • \(D_k = 2^k – 1\) ： 相邻元素互质
  • 最坏情况： \(T = Θ ( N^{3/2} )\)
  • 猜想：\(T_{avg} = O ( N^{5/4} )\)
• Sedgewick增量序列
  • {1, 5, 19, 41, 109, … }
  • \(9*4^i – 9*2^i + 1\) 或 \(4^i – 3*2^i + 1\)
  • 猜想：\(T_{avg} = O ( N^{7/6} )\)，\(T_{worst} = O ( N^{4/3} )\)