Linux 虚拟内存系统
首先,对 Linux 的虚拟内存系统做一个概述,以了解一个实际的操作系统是如何组织虚拟内存,以及如何处理缺页(page fault)的。
Linux 位为每个进程维护了一个单独的虚拟地址空间,形式如下:
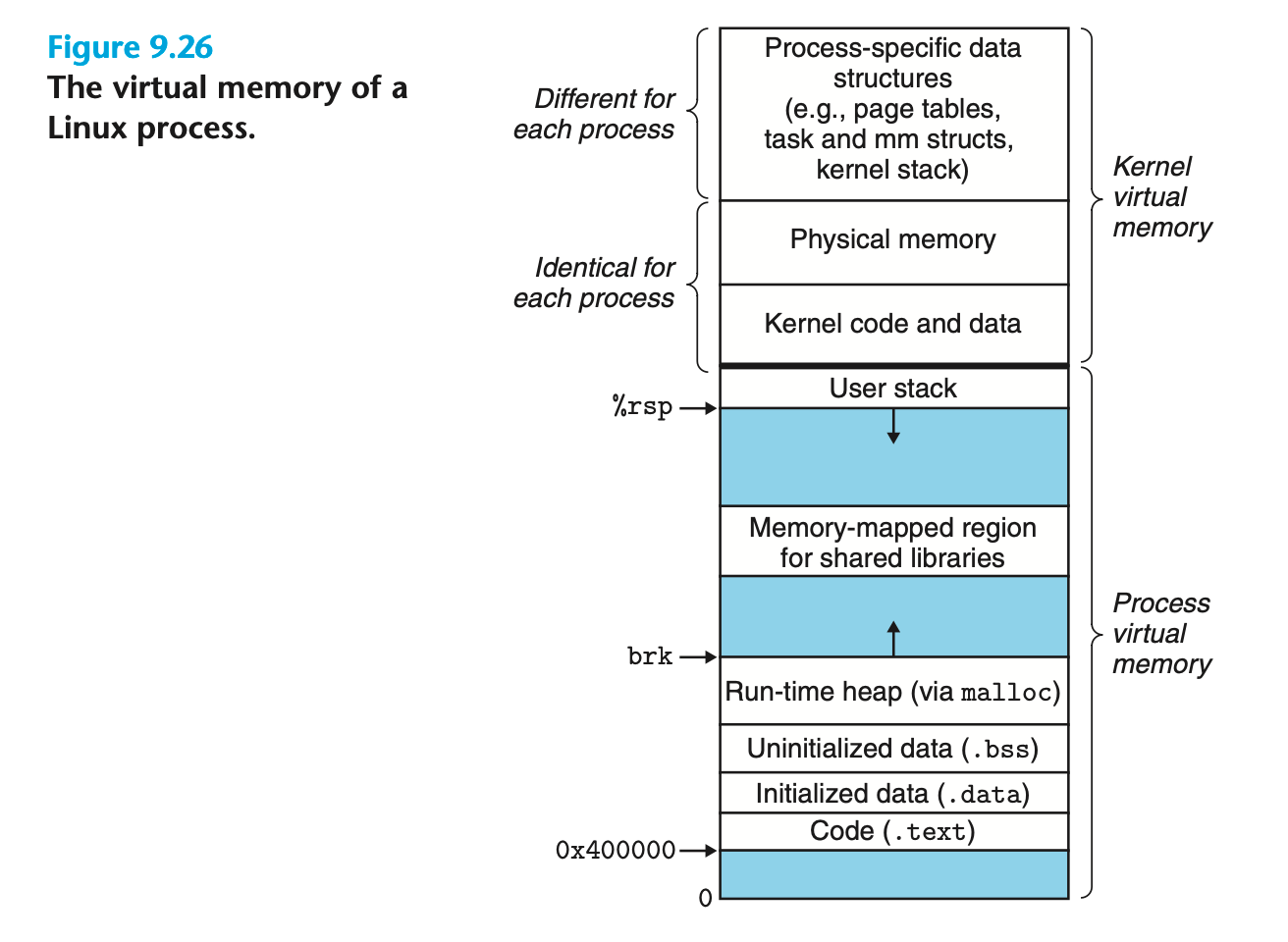
可以看到,虚拟地址空间可以分为内核虚拟内存空间和用户虚拟内存空间两部分,实际上,$64$ 位系统的虚拟空间划分是这样的:
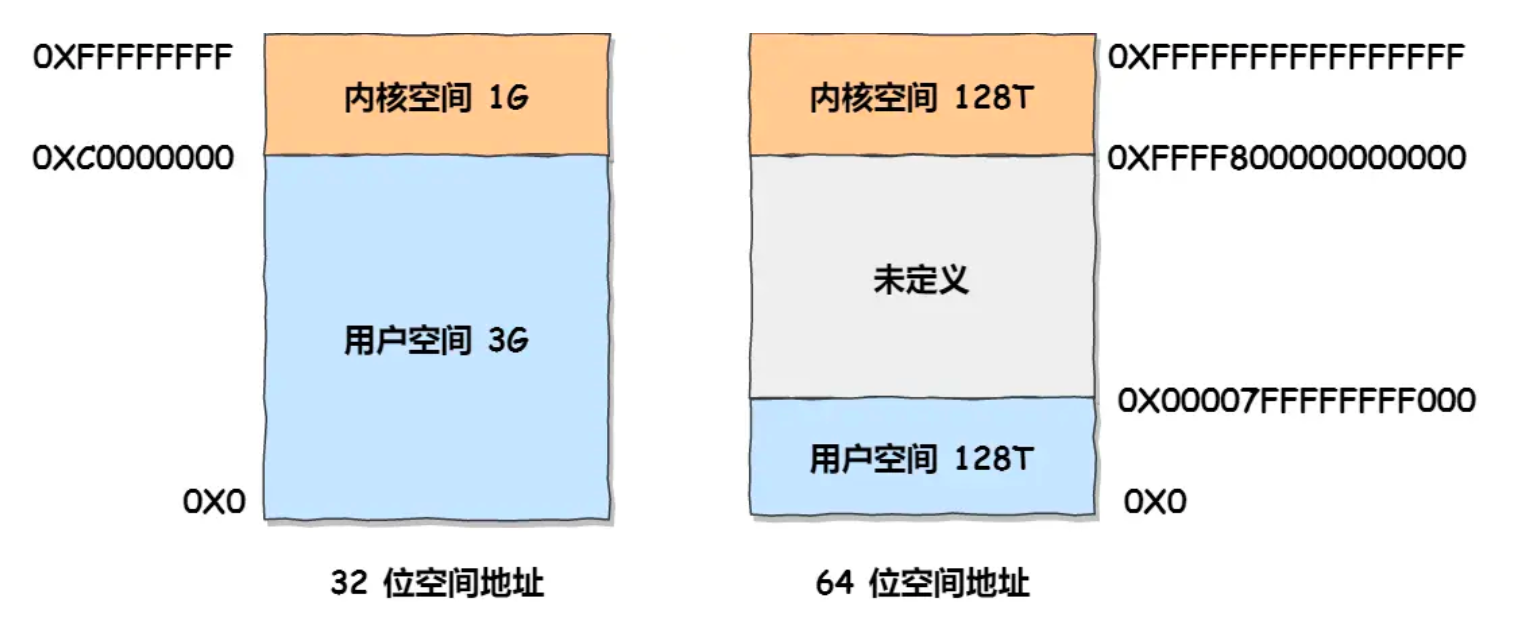
我们可以看到,在用户内存空间和内核内存空间之间还有一大片的“未定义”的区域,这是为什么呢?(注意,后续图片将有灵魂画手出没!)。
之前我们提到,AMD 制定的 $64$ 位 CPU 架构时,虽然是 $64$ 位的,即总的虚拟地址空间是 $64$ 位的,但实际上,用到的虚拟地址其实只有其中的低 $48$ 位。
当我们把
addr_val解释为一个虚拟地址时,我们使用的真正的虚拟地址,其实只有它的低 $48$ 位,(由 AMD 设计 CPU 架构的时候规定,其实 $48$ 位也完全够用了),后 $16$ 位的值会与addr_val的第 $47$ 位保持一致(全 $0$ 或者全 $1$),全 $0$ 表示该虚拟地址处于当前虚拟地址空间的用户态部分,全 $1$ 表示处于内核态部分。
换言之,虚拟地址的高 $16$ 位是由 CPU 在生成要访问的虚拟地址时,先生成低 $48$ 位的虚拟地址,再根据第 $47$ 位的值是 $0$ 还是 $1$,判断地址属于内核虚拟地址空间还是用户虚拟地址空间(或者说进程虚拟地址空间),再生成虚拟地址的高 $16$ 位。
如下图所示:
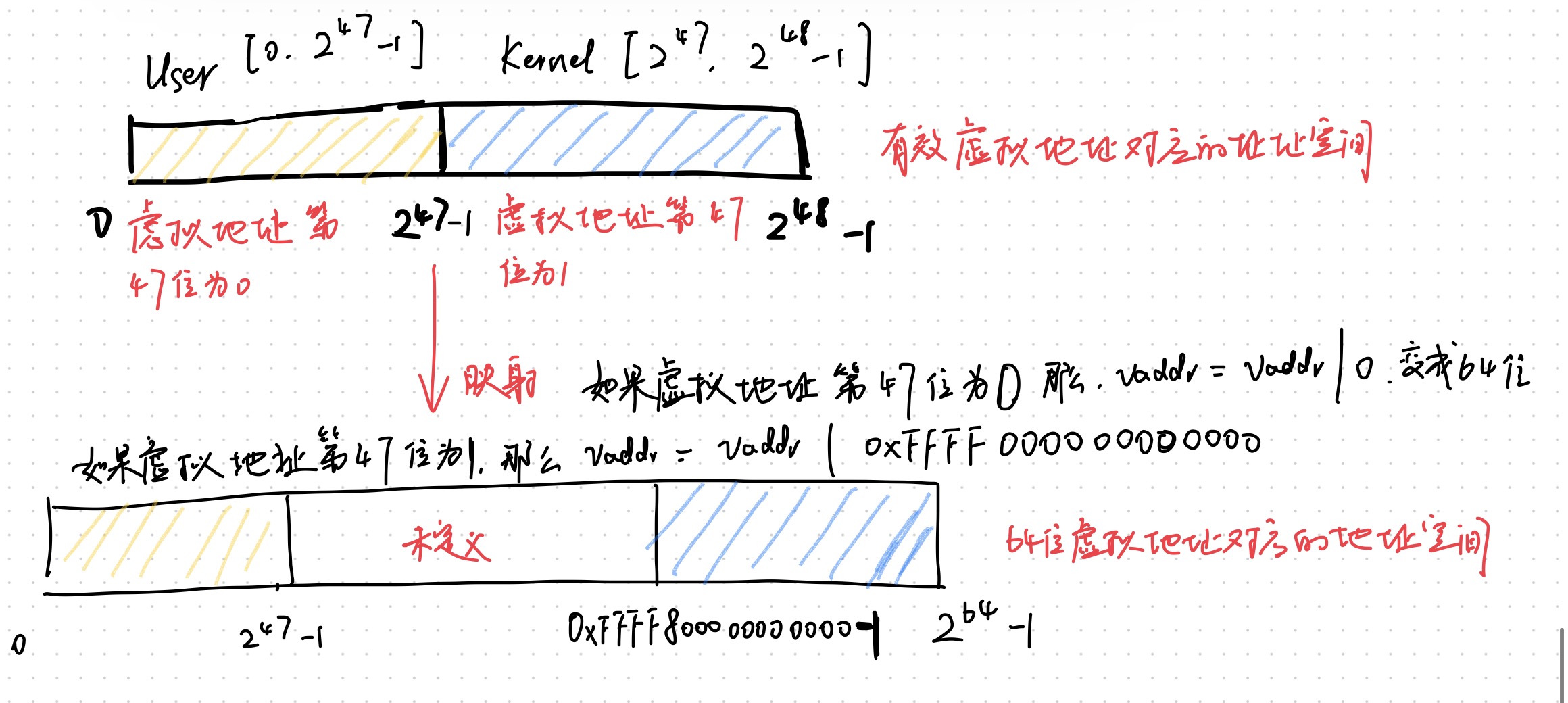
Linux 虚拟内存区域(area)
Linux organizes the virtual memory as a collection of areas (also called segments). An area is a contiguous chunk of existing (allocated) virtual memory whose pages are related in some way. For example, the code segment, data segment, heap, shared library segment, and user stack are all distinct areas.
已分配的虚拟页必然存在于某个 area 中,换言之,不存在于任一 area 的虚拟页是不存在的,对应的虚拟地址是非法的!Heap 中可能存在有多个 area,这些 area 对应的 VP 都是堆上动态创建的数据的虚拟地址对应的 VP。
area 的存在,说明 Linux 系统允许虚拟地址空间有间隙,不存在的虚拟页不会占用内存、磁盘或者内核的任何额外资源。
下图是一个内核用来记录进程的虚拟内存区域的数据结构,这个数据结构存在于内核虚拟内存空间中。
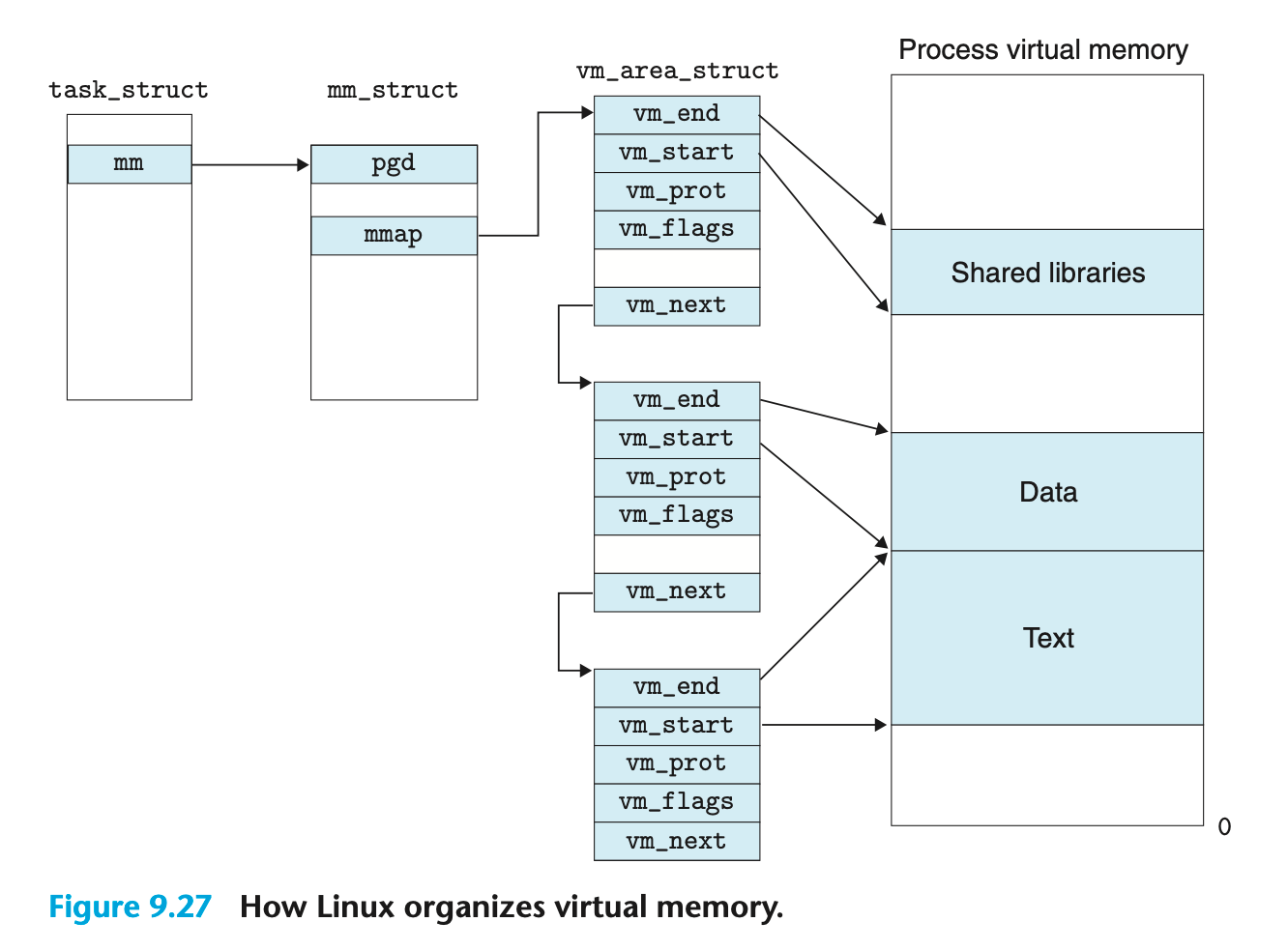
内核为系统中的每一个进程维护一个单独的 task_struct,task_struct 中的元素包含或者指向(即为指针)内核运行该进程所需要的所有信息(例如 PID、指向用户栈的指针、可执行目标文件的名字以及程序计数器 PC 等)。
task_struct 中的一个条目指向 mm_struct,mm_struct 描述了该进程的当前虚拟内存的状态,mm_struct 包含 pgd 和 mmap 两个字段,pgd 指向 PGD 的基地址,而 mmap 指向一个 vm_area_structs 的链表,该链表的每个 vm_area_struct 都描述了当前虚拟地址空间中的一个区域,一个 vm_area_struct 包含以下字段:
vm_start:指向该区域的起始地址(应该是虚拟地址);vm_end:指向该区域的结束处的地址;vm_prot:描述该区域包含的所有 VP 的读写许可权限;vm_flags:描述这个区域内的页面是与其他进程共享的,还是这个进程私有的(还描述了一些其他的信息);vm_next:指向链表中下一个区域结构;
到这里,我们其实可以大致猜想进程的上下文切换时会发生什么,假设单核 CPU,从进程 $1$ 切换到进程 $2$,那么内核就会将 task_struct2 的 pgd 存放在当前 CPU 的 CR3 中,同时将 CPU 的 rip 寄存器更新为 task_struct2 中的 PC。
Linux 缺页异常处理
假设 MMU 要翻译某个 vaddr,触发了一个 page fault。这个异常会导致控制转移到内核的缺页处理程序,处理程序随后会执行以下步骤:
vaddr是否合法,即vaddr对应的 VP 是否存在于该进程的某个area中?因此缺页处理程序需要搜索vm_areas_structs链表,把vaddr和每个vm_area_struct的vm_start和vm_end进行比较,如果 $vm$$start \leq vaddr < vm$$end$