从0开始机器学习--11.关联规则挖掘基础（概念-频繁项集、关联规则、支持度置信度提升度，经典算法-Apriori、哈希树优化支持计数，关联模式评估与复杂度分析，应用与未来趋势，含代码）

零售行业：分析购物篮数据，揭示商品购买之间的潜在关联。在零售中，分析商品间的购买模式（如{Milk, Diaper} → {Beer}）可以用于优化商品陈列和促销策略。
网络安全：通过分析访问日志挖掘异常模式。关联规则用于分析日志数据，挖掘潜在的攻击模式，如{登录失败，异常IP} → {账户锁定}。
医疗诊断：关联患者症状与疾病，帮助医生制定治疗方案。
推荐系统：根据用户行为挖掘偏好模式，用于个性化推荐。例如“喜欢A的人可能也喜欢B”。

关键概念解析

(1) 项集、频繁项集和关联规则

项集：一组物品的集合。例如，超市中的一笔购买记录可以看作一个项集：{牛奶, 面包, 鸡蛋}。
频繁项集：满足最小支持度阈值的项集。例如，如果项集{牛奶, 面包}出现在60%的交易记录中，且支持度阈值为50%，则该项集是频繁的。
关联规则：形如X → Y的语义表达式，表示“如果购买了X，则很可能购买Y”。

(2) 支持度、置信度与提升度

支持度（Support）：衡量规则覆盖的事务比例。表示项集出现在所有事务中的比例。s(X)=包含X的事务数/总事务数。
置信度（Confidence）：规则的可靠性。即在包含X的事务中同时包含Y的概率。c(X→Y)=s(X∪Y)/s(X)
提升度（Lift）：衡量规则的独立性。提升度越高，关联性越强。l(X→Y)=c(X→Y)/s(Y)

(3) 极大频繁项集与闭项集

极大频繁项集：频繁项集的超集不是频繁的。
闭项集：若一个频繁项集X的直接超集都不具有和它相同的支持度计数，则它是闭项集。

超集是数学集合论中的一个概念。如果一个集合 A 包含另一个集合 B 的所有元素，并且 AAA 可以包含 BBB 之外的其他元素，那么 AAA 被称为 BBB 的超集（Superset）。用符号表示为：

$A \supseteq B$ 表示 B 是 A 的子集，或者说 A 是 B 的超集。

如果 A 包含 B 的所有元素，但 A 至少有一个 B 中不存在的元素，则称 A 是 B 的真超集，记为：

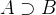
$A \supset B$

# 定义集合
A = {1, 2, 3, 4}
B = {1, 2}

# 判断超集关系
is_superset = A.issuperset(B)  # True
is_proper_superset = A > B     # True, 真超集

# 输出结果
print(f"A 是 B 的超集: {is_superset}")
print(f"A 是 B 的真超集: {is_proper_superset}")

在关联规则挖掘中的超集

在关联规则挖掘中，频繁项集的超集指的是包含某频繁项集的所有项集。例如：给定 B={Milk,Bread}，A={Milk,Bread,Diaper}是 B 的超集。

频繁项集的性质

反单调性（Apriori性质）：如果一个项集 A 不是频繁的，则它的所有超集 A′⊃A也不可能是频繁的。这一性质用于减少算法中的计算开销。

超集在剪枝中的应用

在 Apriori 算法中，生成候选项集后，需要检查哪些候选项集不符合支持度条件。如果某项集不是频繁的，其所有超集也会被直接剪掉，从而避免不必要的计算。

极大频繁项集v.s.闭项集

代码示例：

以下代码通过Python模拟一个购物篮数据集，并计算指定规则的支持度、置信度与提升度：

import pandas as pd

# 模拟事务数据
data = {
    'TID': [1, 2, 3, 4, 5],
    'Items': [
        {'Milk', 'Bread', 'Diaper'},
        {'Bread', 'Diaper', 'Beer', 'Eggs'},
        {'Milk', 'Diaper', 'Beer', 'Coke'},
        {'Bread', 'Milk', 'Diaper', 'Beer'},
        {'Bread', 'Milk', 'Diaper', 'Coke'}
    ]
}
df = pd.DataFrame(data)

# 计算支持度
def calculate_support(itemset, df):
    total_transactions = len(df)
    count = sum(itemset <= row for row in df['Items'])
    return count / total_transactions

# 计算置信度
def calculate_confidence(X, Y, df):
    support_X = calculate_support(X, df)
    support_XY = calculate_support(X | Y, df)
    return support_XY / support_X

# 计算提升度
def calculate_lift(X, Y, df):
    confidence = calculate_confidence(X, Y, df)
    support_Y = calculate_support(Y, df)
    return confidence / support_Y

# 规则 {Milk} -> {Diaper}
X = {'Milk'}
Y = {'Diaper'}
support = calculate_support(X | Y, df)
confidence = calculate_confidence(X, Y, df)
lift = calculate_lift(X, Y, df)

print(f"支持度: {support:.2f}")
print(f"置信度: {confidence:.2f}")
print(f"提升度: {lift:.2f}")

运行结果：

支持度: 0.60
置信度: 1.00
提升度: 1.25

支持度表明规则覆盖了60%的事务。
置信度表示在购买牛奶的事务中，100%也包含尿布。
提升度>1，说明购买牛奶与购买尿布之间有正关联。

经典算法

Apriori算法

Apriori算法基于反单调性原理，通过逐层生成候选项集并剪枝，找到频繁项集。

算法步骤：

从所有1项集开始，计算支持度，筛选出频繁1项集。
利用频繁(k-1)项集生成候选k项集。
剪枝：剔除包含非频繁子集的候选项集。
扫描数据库，计算支持度并生成频繁k项集。
重复以上步骤，直到没有新的频繁项集生成。

from itertools import combinations

# Apriori算法核心函数
def apriori(df, min_support):
    transactions = df['Items'].tolist()
    total_transactions = len(transactions)
    
    # 计算支持度
    def get_support(itemset):
        count = sum(itemset <= t for t in transactions)
        return count / total_transactions
    
    # 初始频繁1项集
    single_items = {frozenset([item]) for transaction in transactions for item in transaction}
    frequent_itemsets = {item: get_support(item) for item in single_items if get_support(item) >= min_support}
    
    # 迭代生成频繁项集
    k = 2
    while frequent_itemsets:
        print(f"频繁{k-1}项集: {frequent_itemsets}")
        # 生成候选k项集
        candidate_k = {i | j for i in frequent_itemsets for j in frequent_itemsets if len(i | j) == k}
        # 计算支持度
        frequent_itemsets = {item: get_support(item) for item in candidate_k if get_support(item) >= min_support}
        k += 1


apriori(df, min_support=0.4)

后续还可以通过将频繁项集大小与支持度绘制成折线图，可以观察支持度阈值对频繁项集的影响。

关联规则生成

从频繁项集中生成关联规则的核心是枚举每个项集的非空子集并计算置信度。若置信度满足最小阈值，则保留该规则。

基于Apriori的规则生成：

使用哈希树优化支持计数

哈希树通过将候选项集映射到哈希桶中，大幅减少比较次数。事务只需与同一哈希桶中的候选项集进行匹配，极大提高了效率。

高级算法与优化

FP-Growth算法：FP-Growth通过构建频繁模式树避免了多次数据库扫描，适合大数据集。

模式压缩：通过极大频繁项集与闭项集的压缩表示，减少存储开销。

关联模式的评估方法

关联规则挖掘生成大量规则，需要进一步量化评估。除支持度和置信度外，以下度量指标也常被使用：

兴趣度（Interest）：
$I(X \to Y) = \frac{P(Y|X)}{P(Y)}$
表示X和Y之间的关联强度。
PS度量：
$PS = P(X \cap Y) - P(X)P(Y)$
衡量规则的非独立性。
f相关系数：用于度量规则的线性相关性。

局限性

支持度和置信度未考虑随机性影响。
仅依赖这些指标可能导致虚假模式的产生，如“高支持度的项集总是关联”的错觉。（即辛普森悖论，在本专栏《10》中有具体介绍）

性质

对称性
- 对称的度量：支持度、兴趣因子/提升度、 f相关度、PS、余弦相似度、Jaccard系统等
- 不对称的度量：置信度、互信息、基尼指数等
缩放性
反演性
零加性：对所有对象进行零加操作，度量值不变
- 具有零加性的度量：支持度、余弦相似度、Jaccrad系数等
- 不具有零加性的度量：f相关度、兴趣因子等

复杂度分析

关联规则挖掘的计算复杂度主要受到以下因素影响：

事务数目和维度：事务数目越多，维度越高，算法的计算量越大。
支持度阈值：较低的支持度阈值会生成更多频繁项集，导致复杂度增加。
数据稀疏性：稠密数据集中的项集组合更为复杂。

优化方向

采用压缩表示法，如极大频繁项集或闭项集。
使用分布式计算框架，如MapReduce。

挑战与前沿方向

(1) 倾斜支持度分布

在大数据集中，大多数项的支持度很低，而少数项的支持度很高（倾斜支持度）。这种分布导致规则挖掘面临以下问题：

高支持度项可能掩盖低支持度项的模式。
低支持度阈值增加计算量。

解决方案：

引入H置信度（全置信度）指标，以避免虚假模式。
识别并处理交叉支持模式。

(2) 高维数据挖掘 随着数据维度的增加，事务之间的重叠减少，导致频繁项集稀疏。研究重点在于开发更加高效的算法，如FP-Growth。

数据挖掘的未来趋势

随着数据规模和复杂度的不断增加，关联规则挖掘的研究正朝以下方向发展：

深度学习结合挖掘：利用深度学习模型增强规则的生成与筛选。
实时模式挖掘：实现对流数据的实时挖掘。
隐私保护数据挖掘：开发保证用户隐私的关联规则挖掘方法。

关联规则挖掘的意义不仅在于模式发现，更在于为商业决策和科学研究提供数据支撑。未来，随着技术的进步和算法的优化，其应用范围将更加广泛。

总结

关联规则挖掘是信息化时代挖掘数据价值的重要工具，通过分析数据中的潜在模式，为实际问题提供解决方案。在算法层面，Apriori通过反单调性实现剪枝，FP-Growth利用频繁模式树大幅提高效率；在性能优化上，压缩表示和分布式计算成为突破复杂度的关键。在评估模式时，综合多维度量化指标，避免偏差或虚假关联。此外，面对倾斜支持度分布、高维数据等挑战，研究人员提出了多种创新方案，如引入H置信度和开发高效算法。未来，深度学习、实时挖掘和隐私保护技术将进一步扩展关联规则挖掘的应用场景，为解决复杂数据问题提供更强有力的支持。

标签：置信度,支持,项集,频繁,规则,关联
From： https://blog.csdn.net/m0_73752612/article/details/143841369