引言
前面我们讲过堆的基本操作的实现,现在给定一个int类型的数组,里面存放的数据是无序的,我们如何利用堆的思想来实现数组内数据的升序排列或降序排列呢?
通过前面讲到的堆的实现,我们可以想到,我们再开辟一块空间来模拟堆,将给定数组里的数据一一插入堆中(pushHeap)。这样做可以是可以,但如果是代码量未免有点大,而且还要额外开辟空间。如果是在平时考试时碰到这种题,那实现起来会有点麻烦。
如果能在给定数组上直接调整并减少点代码量就好了,今天我们就来讲讲如何这样实现堆排序。
堆排序主要涉及到两个步骤:1.建堆 2.利用堆的思想排序(具体怎么排序后面会讲)
接下来我们以排升序为例进行讲解。
如何建堆?
以建大堆为例:
如果是在原数组的基础上进行建大堆,通过前面的堆的学习和实现,我们可以通过在原数组进行向上调整法或向下调整法达到目的。
向上调整法建堆
我们以这个数组为例:
int a[7]={30,60,56,80,70,10,15};
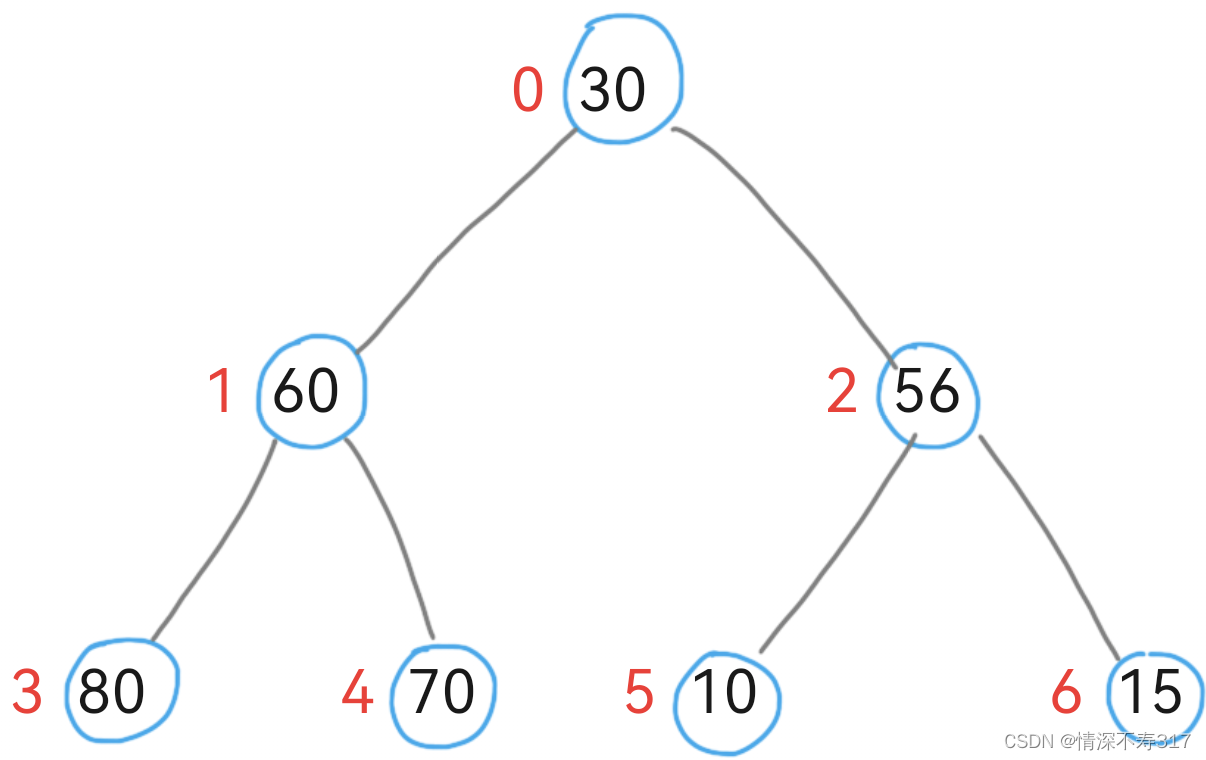
要将它建成大堆:

从下向上遍历:从数组的第二个元素(下标为1)开始,依次向上遍历到第一个元素(下标为0)。这是因为堆的第一个元素(根节点)在构建过程中不需要进行向上调整。
向上调整:对于遍历到的每个元素(假设当前元素的下标为i),执行以下步骤:
- 计算当前元素的父节点下标(parent = (i - 1) / 2)。
- 比较当前元素与其父节点的值。
- 如果当前元素的值大于其父节点的值,则交换这两个元素的位置。
- 交换后,将当前元素的下标更新为其父节点的下标,并重复上述比较和交换步骤,直到当前元素的值不大于其父节点的值,或者当前元素成为根节点。
- 完成建堆:当遍历完所有元素并完成所有必要的向上调整后,整个数组就形成了一个大顶堆。
附上代码:
void swap(dataType* x, dataType* y)
{
dataType tmp = *x;
*x = *y;
*y = tmp;
}
void adjustUp(dataType* a, int child)
{
assert(a);
int parent = (child - 1) / 2;
while (child > 0) {
if (a[child] > a[parent])
{
swap(&a[parent], &a[child]);
child = parent;
parent = (child - 1) / 2;
}
else {
break;
}
}
}
void heapSort(int* a, int n) {
for (int i = 1; i < n; i++) {
adjustUp(a, i);
}
}向下调整法建堆
还是以原来的数组为例:
int a[7]={30,60,56,80,70,10,15};
将它建成大堆:
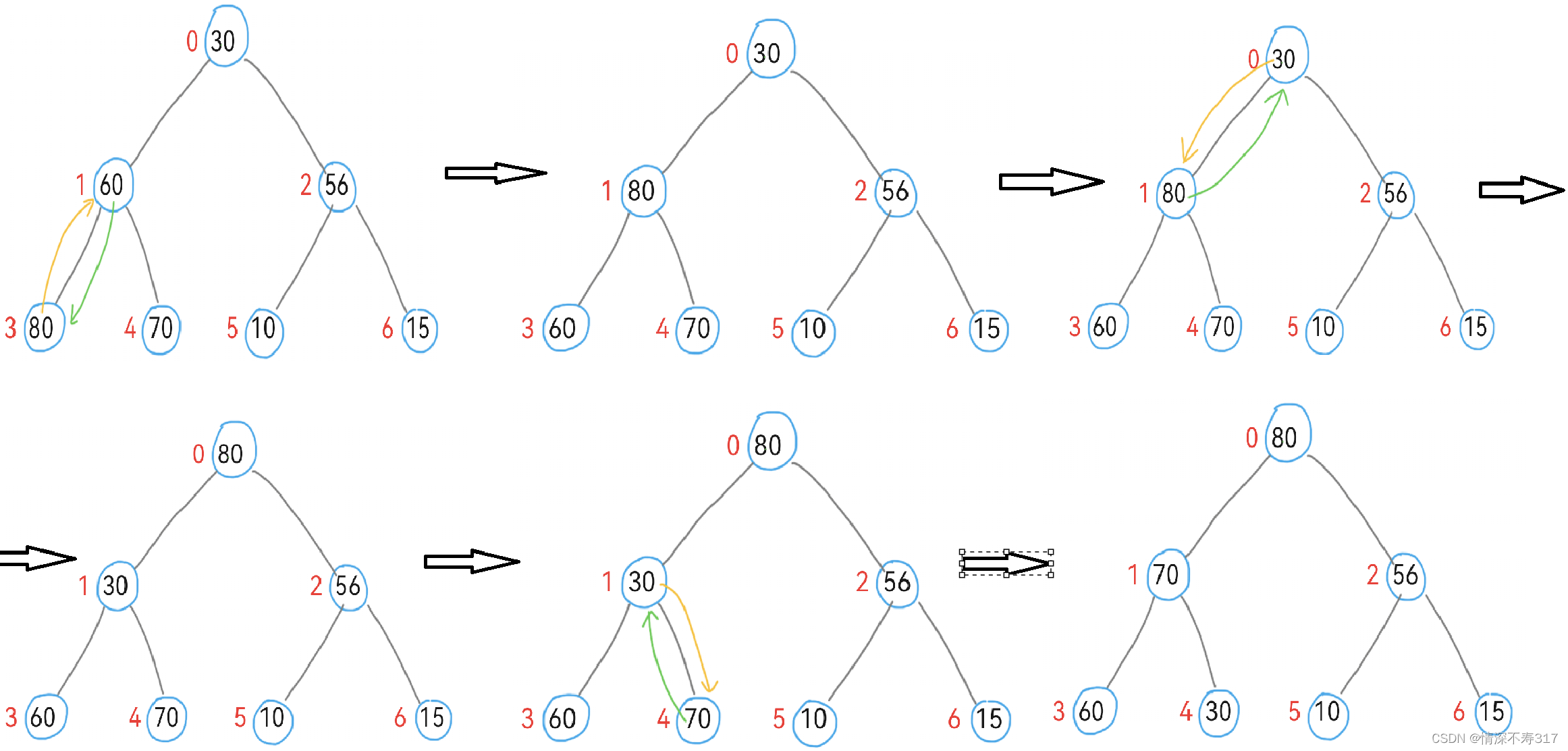
从最后一个非叶子节点开始,依次向上遍历每个节点(包括根节点)。对于每个节点,执行以下步骤:
- 将当前节点视为父节点。
- 比较其父节点与左右子节点的值(如果存在的话)。
- 如果父节点的值小于左右子节点中的较小值,则交换父节点与较小子节点的值。
- 将交换后的较小子节点视为新的父节点,重复上述比较和交换步骤,直到父节点的值大于或等于其所有子节点的值,或者父节点成为叶子节点。
当所有节点都按照上述步骤调整完毕后,整个数组就形成了一个大顶堆。
这里有一个问题,如何算最后一个出非叶子节点的下标呢?
在一个堆中,最后一个叶子节点的下标是n-1,那它父节点的下标就是(n-1-1)/2也就是(n-2)/2。
附上代码:
void swap(dataType* x, dataType* y)
{
dataType tmp = *x;
*x = *y;
*y = tmp;
}
int getMax(dataType* a, int x, int y)
{
if (a[x] > a[y])
{
return x;
}
else {
return y;
}
}
void adjustDown(dataType* a, int parent, int size)
{
assert(a);
while (parent < size)
{
int lChild = 2 * parent + 1, rChild = 2 * parent + 2, swapChild;
if (rChild < size) {
swapChild = getMax(a, lChild, rChild);
}
else {
swapChild = lChild;
}
if (swapChild < size && a[parent] < a[swapChild]) {
swap(&a[parent], &a[swapChild]);
parent = swapChild;
}
else {
break;
}
}
}
void heapSort(int* a, int n) {
//向下调整法
for (int i = (n - 2)/2; i >= 0; i--) {
adjustDown(a, i, n);
}
}时间复杂度
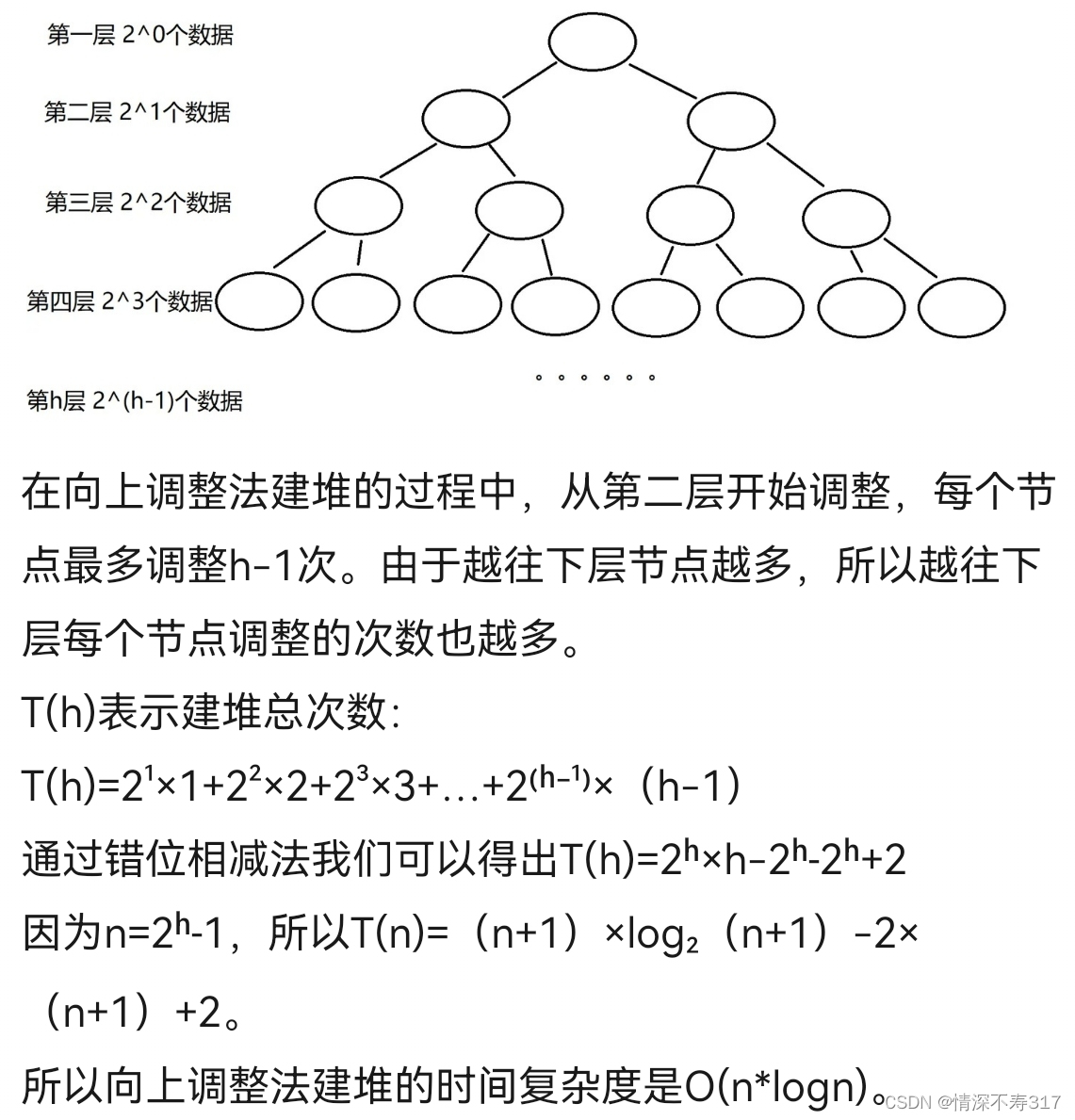
向上调整法建堆
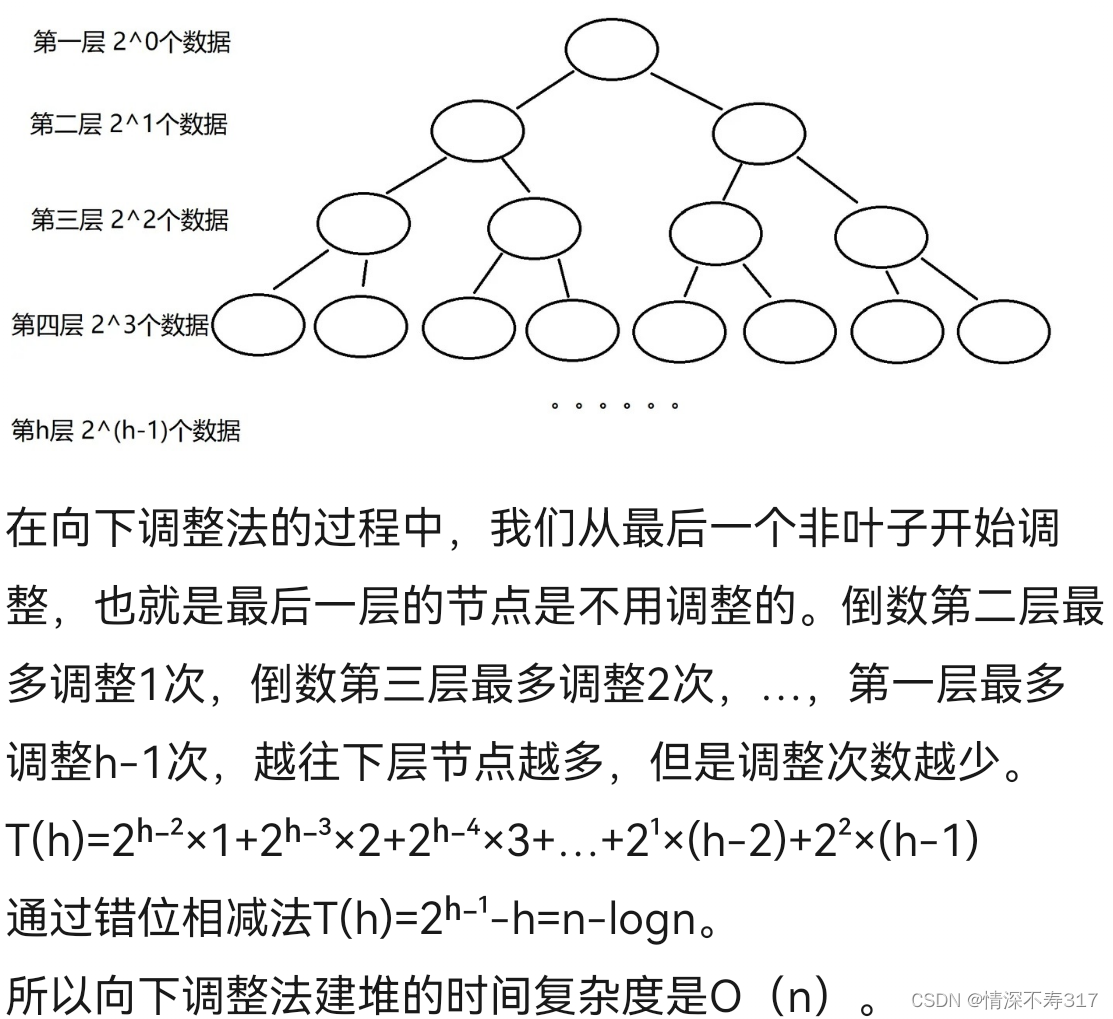
向下调整法建堆
总结
对比之下,向下调整法建堆的时间复杂度更低,所以我们更推荐用向下调整法建堆。
一个误区:排升序就是直接将原来无序的数组构建成小堆就可以了
说到建堆,无非就两种:要么建大顶堆,要么建小顶堆。但如果是排升序,很多人可能第一反应是直接建小顶堆就可以了。但是这样真的合适吗?我们以这个数组为例:
int a[5]={30,60,56,70,10};
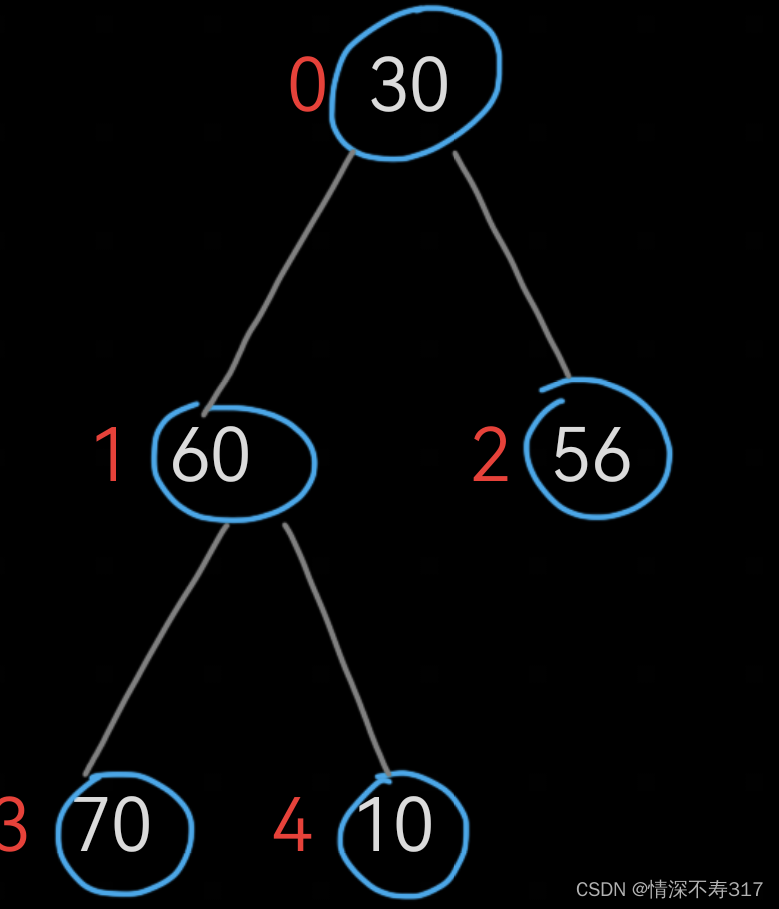
把它建成小顶堆会是这样:
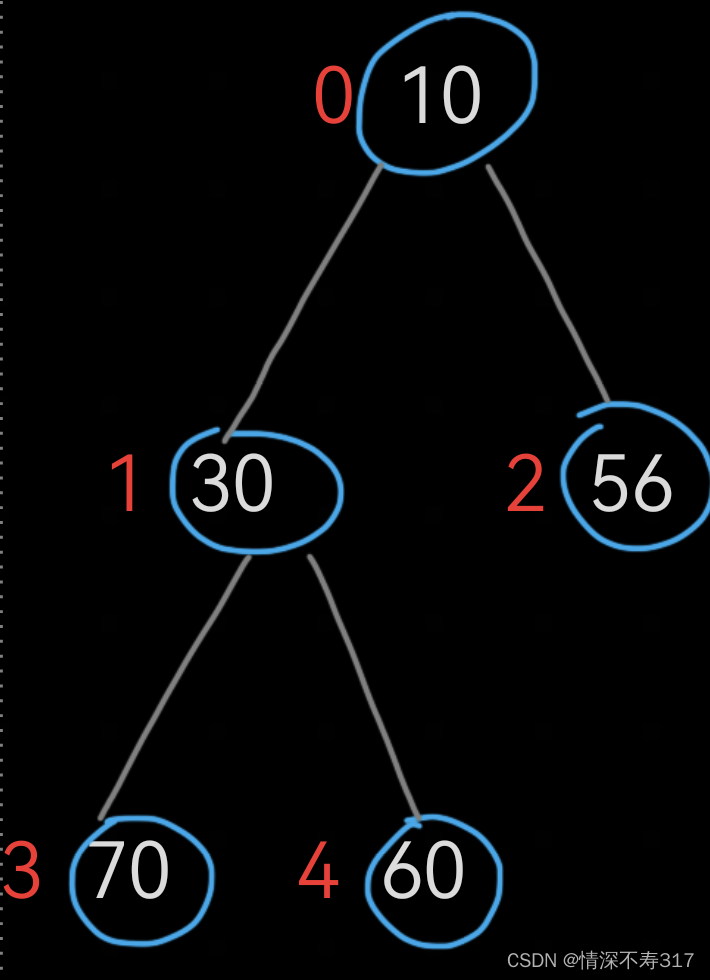
对应的数组就是这样了:int a[5]={10,30,56,70,60};
我们发现这样调整后,数组里面的数据并不是完全按照升序排列的。为什么会这样呢?
我们需要知道,在小堆中,堆顶元素确实是最小的。但是,这并不意味着从堆顶到堆尾的所有元素都按升序排列。小堆的结构只保证了从根节点到每个叶子节点的路径上,元素是递增的。然而,不同路径上的元素之间并没有这样的保证。
所以,直接将原来无序的数组构建成小堆是不可行的办法。
排升序建大堆,排降序建小堆
那我们该怎么办呢?
答案是:排升序建大堆,排降序建小堆。
竟然跟我们最初的想法背道而驰,接下来我会讲解一下为什么要这么做以及具体如何实现。
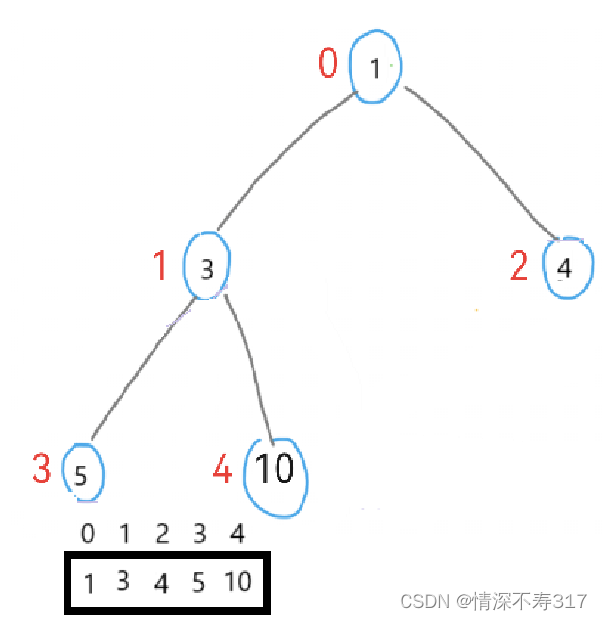
我们以这个数组为例:
int a[5]={4, 10, 3, 5, 1}
具体步骤
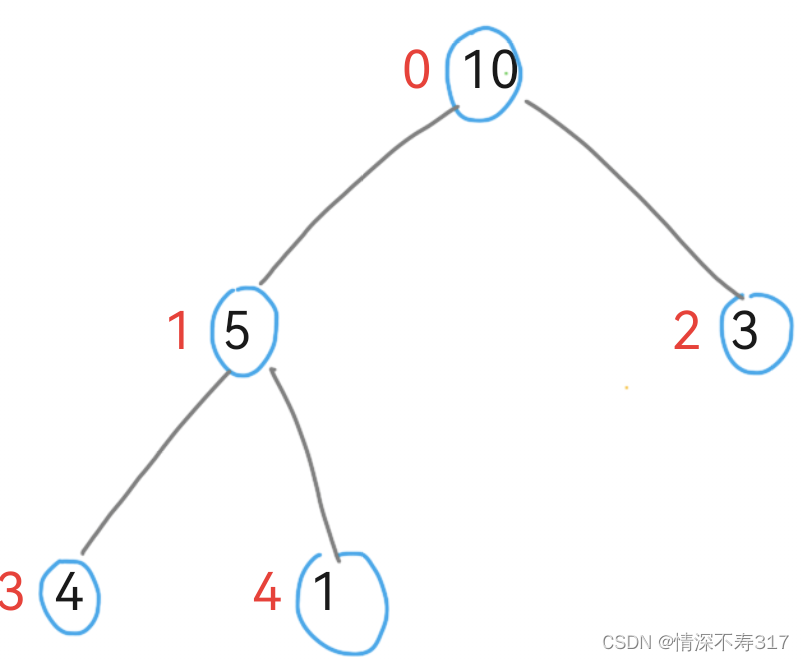
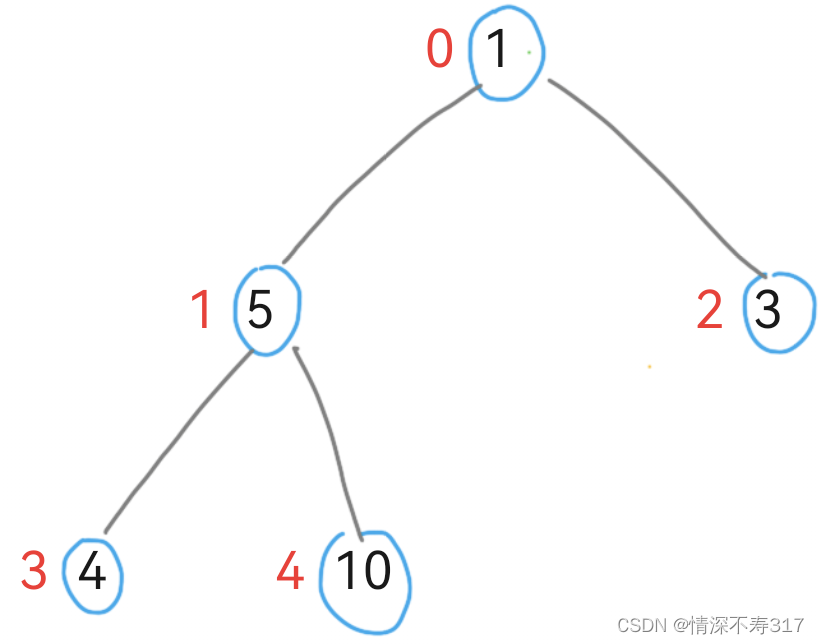
1.我们先把将它建成大堆:
int a[5]={10,5,3,4,10};
2.交换堆顶元素与末尾元素:将堆顶元素(当前最大值)与序列末尾元素交换位置。
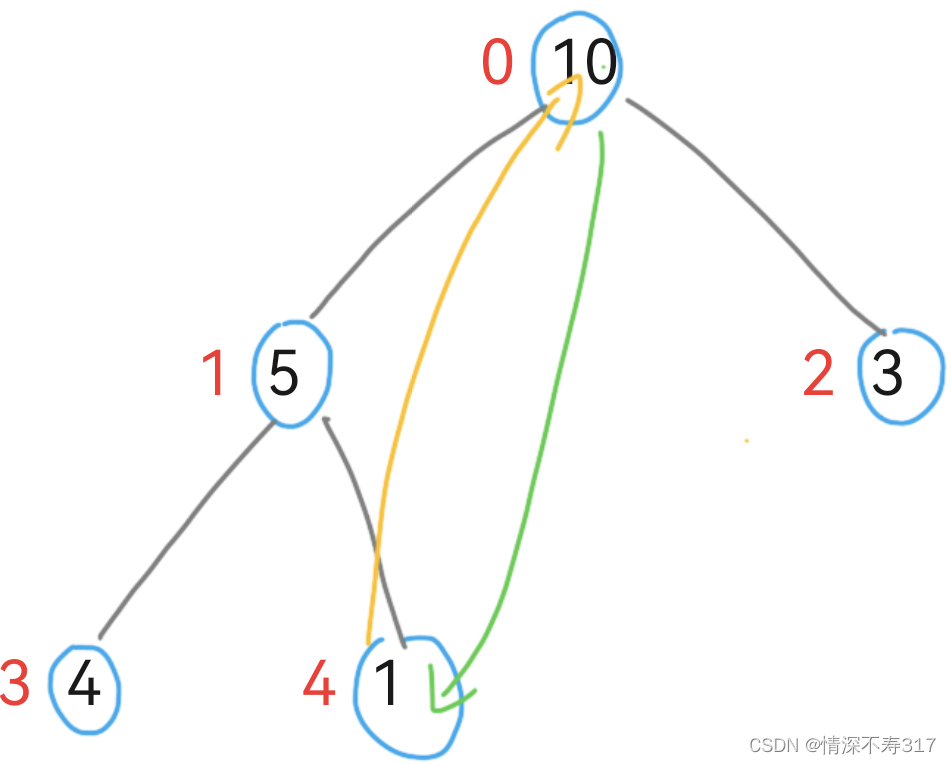
这一步骤将最大值“沉”到底部,同时保证了剩余元素组成的子序列仍满足堆的性质。
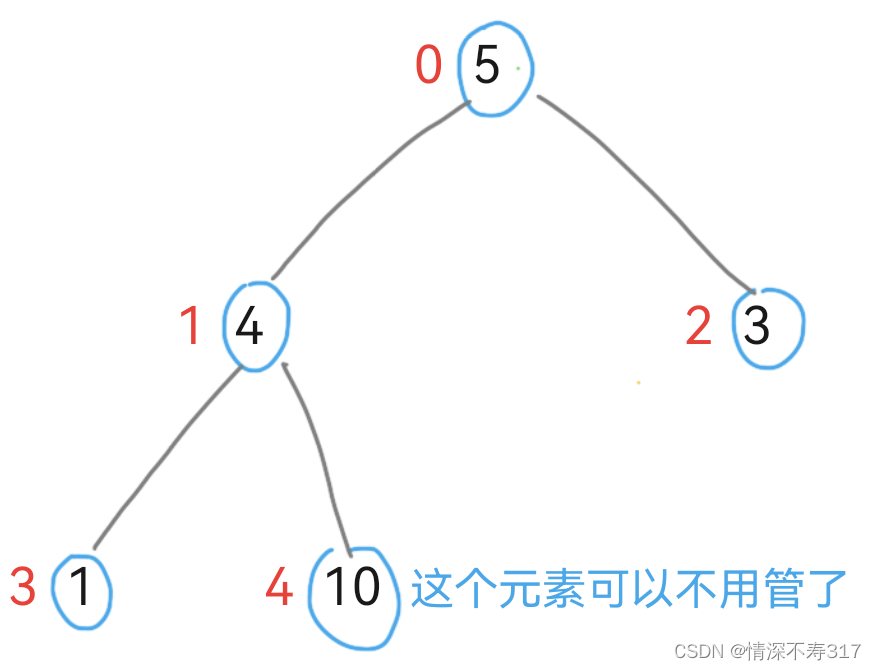
3.调整剩余元素:将交换后的剩余元素(除去已排序的堆顶元素)重新调整为一个堆。
由于堆顶元素已被移到末尾,此时需要对剩余元素重新执行向下调整操作,使得新的堆顶元素成为剩余元素中的最大值。
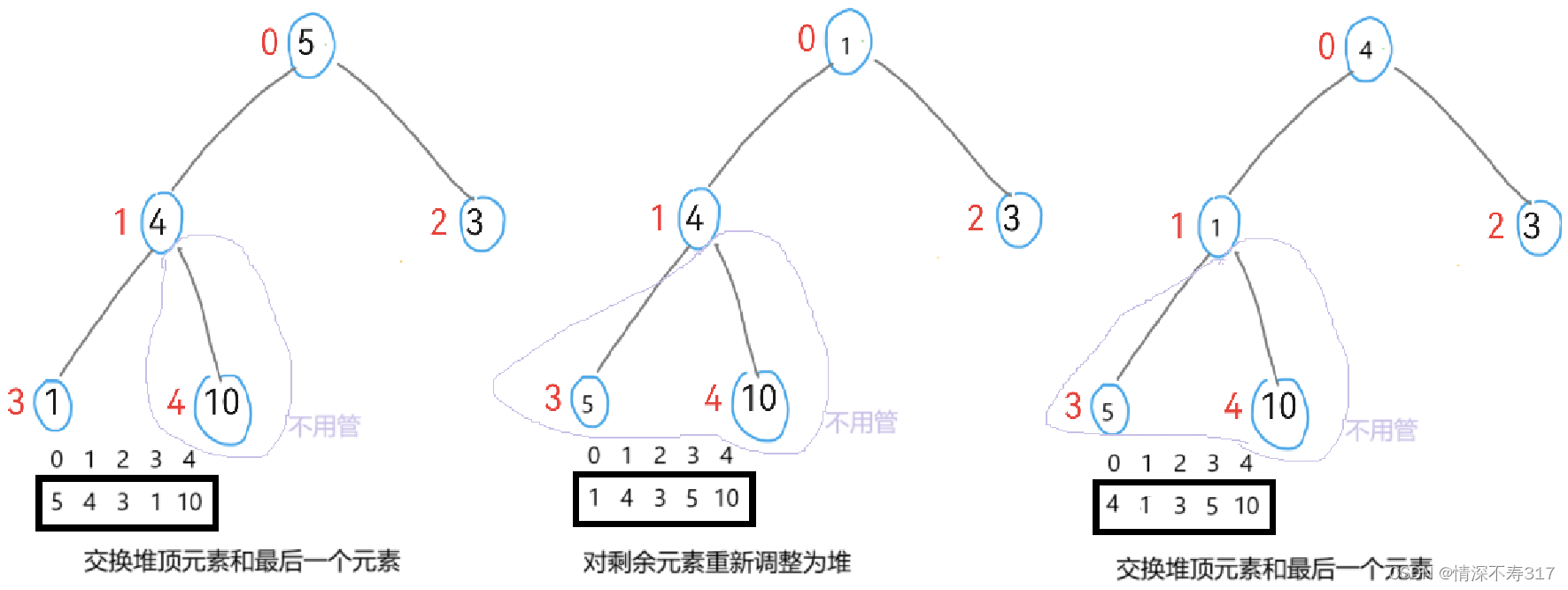
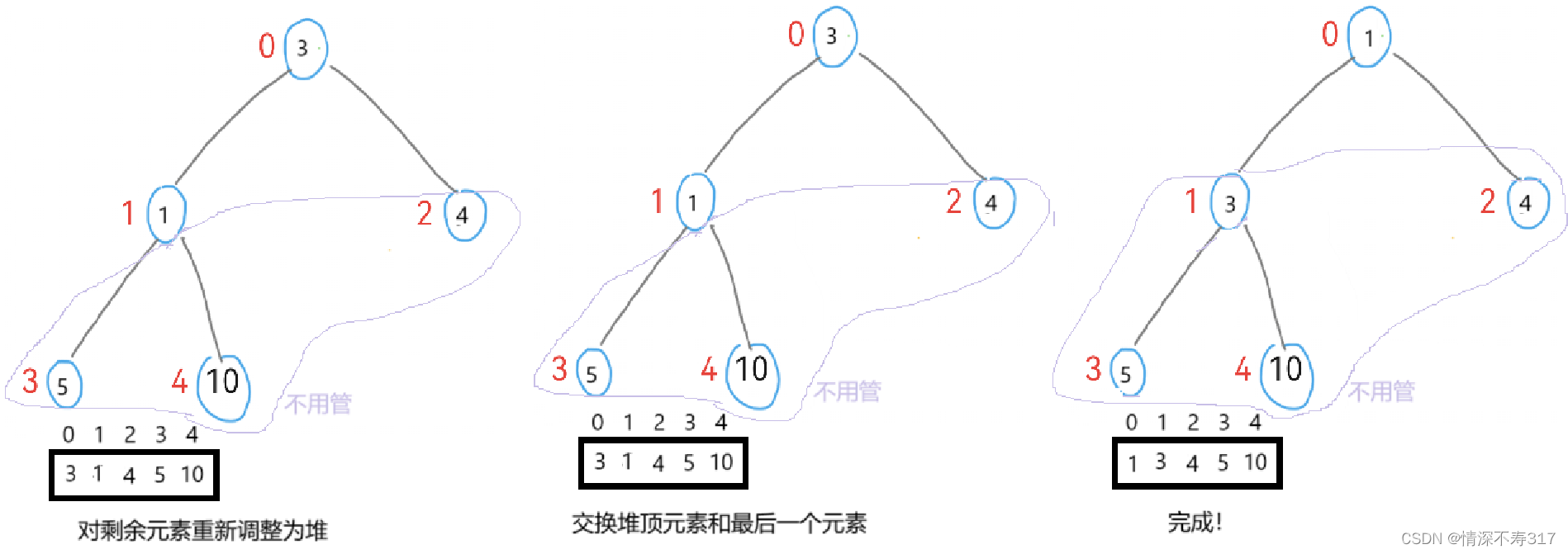
4.重复交换与调整:重复步骤2和步骤3,每次都将当前堆顶元素(即剩余部分的最大值)与末尾元素交换,并对剩余元素重新调整为堆。
① ② ③
 ④ ⑤ ⑥
④ ⑤ ⑥
随着每一次交换和调整,有序序列逐渐扩大,堆的大小逐渐减小。
5.终止条件:当堆的大小减小到1时,整个序列已经有序,堆排序过程结束。
代码
void swap(dataType* x, dataType* y)
{
dataType tmp = *x;
*x = *y;
*y = tmp;
}
int getMax(dataType* a, int x, int y)
{
if (a[x] > a[y])
{
return x;
}
else {
return y;
}
}
void adjustDown(dataType* a, int parent, int size)
{
assert(a);
while (parent < size)
{
int lChild = 2 * parent + 1, rChild = 2 * parent + 2, swapChild;
if (rChild < size) {
swapChild = getMax(a, lChild, rChild);
}
else {
swapChild = lChild;
}
if (swapChild < size && a[parent] < a[swapChild]) {
swap(&a[parent], &a[swapChild]);
parent = swapChild;
}
else {
break;
}
}
}
void heapSort(int* a, int n) {
//向下调整法
for (int i = (n - 2)/2; i >= 0; i--) {
adjustDown(a, i, n);
}
int cnt = n - 1;
while (cnt) {
swap(&a[0], &a[cnt]);
adjustDown(a, 0, cnt);
--cnt;
}
}时间复杂度
前面我们知道,通过向下调整法构建初始堆的时间复杂度为O(n),因为需要对n个元素进行一次向下调整操作。
交换堆顶元素与末尾元素并重新调整堆的过程需要重复n-1次,每次调整的时间复杂度为O(log n)。
因此,总的时间复杂度为O(n log n)。
如果排升序建小堆
在堆排序中,如果目标是进行升序排序,通常我们会选择构建大顶堆,而不是小顶堆。这是因为大顶堆的堆顶元素是最大的,通过不断地将堆顶元素与末尾元素交换并调整堆,可以逐步将序列排序为升序。
然而,如果尝试使用小顶堆来进行升序排序,步骤和弊端如下:
具体步骤
1.建堆:给定一个无序数组int a[5]={4, 10, 3, 5, 1},通过向下调整法将其构建为小顶堆int a[5]={1, 3, 4,5,10};
1
/ \
3 4
/ \
5 10
2.交换与调整:将小顶堆的堆顶元素(当前最小值)与数组末尾元素交换位置。
堆顶元素(1)与数组末尾元素(10)交换:
10
/ \
3 4
/ \
5 1
由于交换后的堆顶元素可能不再是最小值,因此需要对剩余元素重新调整为小顶堆。
对应的数组表示变为:[10, 3, 4, 5, 1],此时,1已经被放到了数组最后的位置,不再参与后续堆化。
但是注意了,剩余元素[10, 3, 4, 5]需要重新调整为小顶堆。但是,不能直接通过下沉操作将3放到堆顶,因为这里的adjustDown函数是从堆顶开始与较大的子节点交换,直到找到合适的位置。在这个情况下,堆顶是10,它是当前堆中的最大值,下沉操作会将它与孩子几点钟较大的那一个孩子节点交换,也就是4,并不能把3交换上去。
正确的重新堆化过程:实际上,我们需要从最后一个非叶子节点开始(在这个例子中是4),向上逐个节点进行堆化,确保每个子树都满足小顶堆的性质。
然后,我们再将根节点(10)与其子节点中较小的一个进行交换,直到整个堆满足小顶堆的性质。
这个过程比简单地下沉操作要复杂得多,因为它可能涉及到多次交换和比较。
3.重复步骤:重复步骤2,每次都将新的堆顶元素(当前最小值)与数组末尾元素交换,并重新调整剩余元素为小顶堆。
弊端(与大顶堆相比)
一、效率低下
- 小顶堆:
- 每次交换到末尾的是当前最小值。
- 需要对整个堆进行重新调整以得到下一个最小值。
- 迭代过程中每次都需要进行调整,导致整体效率低下。
- 大顶堆:
- 每次交换到末尾的是当前最大值。
- 剩余元素自然形成新的堆,只需对堆顶元素进行向下调整。
- 每次迭代的时间复杂度相对较低。
二、稳定性问题
- 小顶堆升序排序时,每次交换最小值可能破坏相同元素的相对顺序,稳定性问题更突出。
三、逻辑复杂性
- 小顶堆用于升序排序反直觉。
- 升序排序目标为从小到大排列,大顶堆堆顶为当前最大值,更符合需求。
- 小顶堆需每次交换后进行复杂调整操作。
ps:在第一次学习数据结构的时候,我并没有学过堆排序。这篇博客也是本人到目前为止写的最心累的一篇博客!其实如果掌握好了前面堆的实现的内容,堆排序理解和实现起来并不难。所以前面的内容一定要理解到位!
标签:parent,int,元素,堆排序,算法,数组,升序,节点 From: https://blog.csdn.net/2403_82706967/article/details/144071589