超参数调整、Batch归一化和程序框架
超参数调整
-
在深度学习中,有许多超参数需要调整,不同超参数的重要性有所不同,可分为以下优先级:
第一优先级是学习率 \(\alpha\) 。
第二优先级是动量梯度下降参数 \(\beta\) ,隐藏层神经元数量,以及mini-batch大小。
第三个优先级是隐藏层数量,学习率衰减率。
第四个优先级是Adam算法参数,通常无需调整,默认值为\(\beta_1=0.9,\beta_2=0.999,\epsilon=10^{-8}\)。
-
在超参数调整中,可以采用网格取样法(Grid Sampling),随机取样法(Random Sampling),粗糙到精细采样法(Coarse-to-Fine Sampling)。
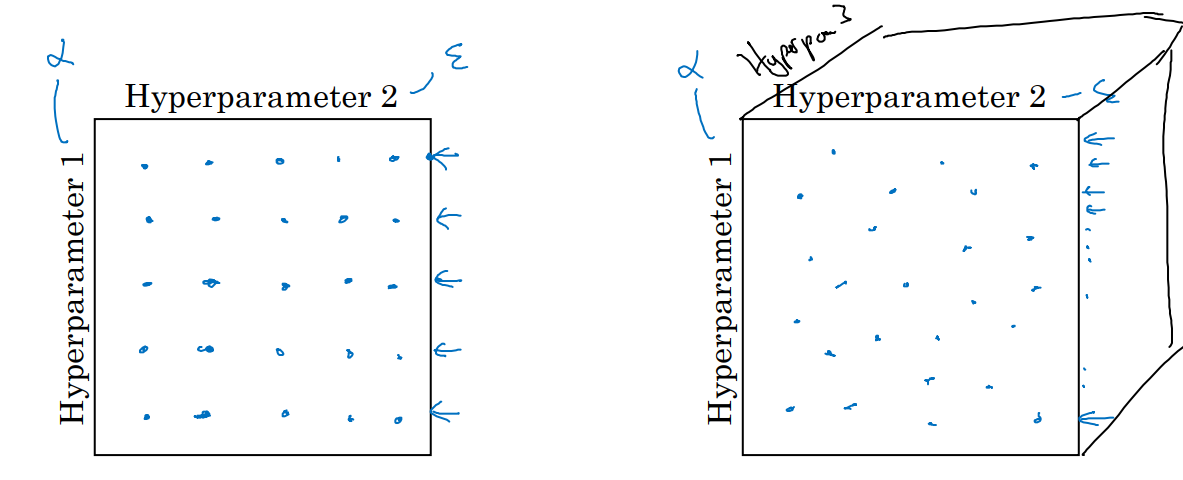
网格取样法均匀地取样超参数值(例如,按照固定间隔形成一个网格),然后逐一测试不同组合的效果。适用于参数较少的情况,但如果重要参数分布较窄,会浪费资源。
随机取样法随机选择超参数值进行实验,覆盖更多潜在的超参数组合,适用于参数多且重要性分布未知的情况。可以更高效地探索重要超参数的影响,例如学习率 \(\alpha\) 远比某些次要参数(如 \(\epsilon\) )更重要,随机取样法能在重要超参数上分配更多探索空间。
粗糙到精细采样法先进行粗略的超参数取样,找到表现较好的区域后,集中在该区域进行更密集的搜索。
-
在调整超参数范围时,需要映射到合适的比例范围,以保证取样的有效性。不同的超参数需要采用不同的取值方法:
隐藏层神经元数量可以从 \([50, 100]\) 的范围内随机均匀取值。
隐藏层数通常取值范围为 \([2, 4]\),可以随机均匀地选择整数值(例如 2、3、4)。
学习率 \(\alpha\) 范围通常为 \([0.0001, 1]\),如果在此范围内随机均匀取值,90%的数值会集中在\([0.1, 1]\),导致对低值(如 \([0.0001, 0.1]\) )的搜索不足。为避免这种问题,应在对数轴上取值,转换为 \([10^{-4}, 10^{0}]\),对应对数范围 \([-4, 0]\)。在此对数范围内均匀随机取值,可以更合理地分配搜索资源。
动量梯度下降法参数 \(\beta\) 范围为 \([0.9, 0.999]\),直接在线性轴上随机均匀取值不合理,因为靠近 1 的 \(\beta\) 对算法性能的影响更显著。更合理的方法是搜索 \(1-\beta\) 的对数值,将范围映射到 \(\text{log}(1-\beta)\) 的区间 \([-3, -1]\),然后在此对数范围内均匀随机取值。
对于大多数超参数(如 \(\alpha\), \(\beta\)),在对数轴上取值能更均匀地覆盖有效范围,提升搜索效率。对于离散参数(如隐藏层数),直接在整数范围内随机均匀取值较为合理。靠近某些边界值(如 \(\beta \to 1\))时,超参数对结果的影响会显著增加。因此,应在灵敏度较高的区域加密取值。
-
根据计算资源的多寡,超参数搜索过程可分为以下两种主要方式:
- 第一种是熊猫模式,适用于计算资源有限,无法同时试验多个模型,数据规模较大,或模型训练时间较长的情况。这种模式一次只试验一个模型,在试验过程中,通过观察模型的表现(如损失函数曲线或误差曲线)逐步调整超参数。过程较为细致,每次调整需要较长时间。很适合资源受限的情况,便于深入理解单个模型的表现。但是调参过程较慢,覆盖的超参数空间有限。
- 第二种是鱼子酱模式,适用于计算资源充足,可以同时运行多个模型的情况。这种模式平行试验多组超参数设定,训练多个模型,通过比较所有模型的损失函数曲线,快速选择表现最好的超参数组合。能快速覆盖更大的超参数空间,增加找到最优参数的可能性,但是对计算资源要求较高。
Batch归一化
-
输入特征归一化可以加速学习过程,提高优化效率。在传统机器学习中,对输入特征 \(X\) 进行归一化(零均值和单位方差处理)能够改善模型的训练性能。在深度学习中,可以对隐藏层激活值进行归一化,以提升学习效率,尤其是对深层神经网络。实践中,通常对隐藏层线性变换的输出 \(z^{[i]}\) 进行归一化,而非激活值 \(a^{[i]}\) 。
\[ \mu = \frac{1}{m}\sum_{i=1}^{m}z^{[l](i)} \\ \sigma^2=\frac{1}{m}\sum_{i=1}^m(z^{[l](i)}-\mu)^2 \\ z_{\text{norm}}^{[l](i)}=\frac{z^{[l](i)}-\mu}{\sqrt{(\sigma^2+\epsilon)}} \]
对于第 \(l\) 层隐藏单元 \(z^{[l]}\) ,假设其共有 \(m\) 个样本值:为了使隐藏单元拥有更多样的分布(而非固定的零均值和单位方差),引入可学习的线性变换:
\[ \widetilde{z}^{[l](i)}=\gamma z_{\text{norm}}^{[l](i)} + \beta \]\(\gamma \in \mathbb{R}^{n^{[l]\times1}}\) 控制方差, \(\beta \in \mathbb{R}^{n^{[l]\times1}}\) 控制均值,这两个参数通过反向传播与神经网络的其余参数一同学习。特殊情况下,如果 \(\gamma = \sqrt{\sigma^2 + \varepsilon}\) , \(\beta = \mu\),则归一化过程退化为恒等映射,即 \(\widetilde{z}^{[l]} = z^{[l]}\) 。
对于激活函数如Sigmoid等线性范围较小的函数,通过 \(\gamma\) 和 \(\beta\) 调整隐藏单元的分布,可以更充分利用激活函数的非线性特性。
-
在神经网络中,Batch归一化对每个隐藏层的线性变换输出 \(z^{[l]}\) 进行归一化和重新缩放,然后输入激活函数 \(a^{[l]}\) 进行后续计算。由于归一化过程会对 \(z^{[l]}\) 的均值进行调整,偏置参数 \(b^{[l]}\) 的作用被抵消。因此,应用Batch归一化后,公式简化为:
\[z^{[l](i)} = w^{[l]}a^{[ l - 1 ](i)} \\ \mu = \frac{1}{m}\sum_{i=1}^{m}z^{[l](i)} \\ \sigma^2=\frac{1}{m}\sum_{i=1}^m(z^{[l](i)}-\mu)^2 \\ z_{\text{norm}}^{[l](i)}=\frac{z^{[l](i)}-\mu}{\sqrt{(\sigma^2+\epsilon)}} \\ \widetilde{z}^{[l](i)}=\gamma z_{\text{norm}}^{[l](i)} + \beta \]在反向传播中,Batch归一化的参数 \(\gamma^{[l]}\) 和 \(\beta^{[l]}\) 通过梯度下降法进行更新。更新公式如下:
\[\omega^{[l]} = \omega^{[l]} -\alpha \omega^{[l]} \\ \beta^{[l]} = \beta^{[l]} - \alpha d\beta^{[l]} \\ \gamma^{[l]} = \gamma^{[l]} - \alpha d\gamma^{[l]} \]Batch归一化可与多种优化算法结合使用,如Momentum、RMSprop、Adam等,进一步提升优化效率。
Batch归一化通常结合mini-batch梯度下降法。在每个mini-batch上,计算均值和方差,对 \(z\) 值进行归一化,并更新参数。在深度学习框架中,Batch归一化通常可以通过调用现成的函数实现(如tf.nn.batch_normalization),大大简化了实现过程。 -
Covariate Shift问题:如果隐藏层前一层的分布发生变化,后续层需要重新适应这些变化,导致训练过程变慢。
在深层网络中,从第三个隐藏层的视角来看,由于前一层参数的更新会改变激活值的分布,那么第三层需要不断调整,增加了学习的难度。Batch归一化通过对隐藏单元的线性变换输出进行归一化并重新缩放,稳定了激活值的分布。这种稳定性减少了网络层间的依赖,使每层可以更加独立地学习,从而加速整体学习。 -
Batch归一化也具有一定的正则化效果。在mini-batch上计算均值和方差会存在一些估计噪声,因为只是由一小部分数据得出。这种噪声类似于给隐藏单元添加了随机扰动,迫使网络不依赖某个特定单元。正如Dropout通过随机遮盖部分单元实现正则化,Batch归一化通过这种随机扰动对模型产生了轻微的正则化效果。
如果采用较小的mini-batch,那么噪声会较大,正则化效果更强。如果采用较大的mini-batch,噪声会减小,正则化效果较弱。虽然Batch归一化有正则化的副作用,但它的主要目的是加速学习,而非正则化。
-
在训练阶段,Batch归一化通过对每个mini-batch的激活值进行归一化来调整隐藏层输出。在测试阶段,模型可能需要逐个样本处理,此时无法像训练阶段那样计算一个mini-batch的均值和方差。因此,在测试阶段需要使用在训练过程中积累的均值和方差的估计值,而不是依赖于当前测试样本的mini-batch计算。
在训练极端,用指数加权移动平均的方式积累每个mini-batch的均值和方差。训练完成后,这些指数加权移动平均值会被用作测试阶段的 \(\mu\) 和 \(\sigma^{2}\)。
通过这种方式,可以在训练阶段积累均值和方差,可以确保模型在训练和测试阶段具有一致性。即使逐个样本进行预测,也能利用整个训练过程中的统计信息,保持预测的可靠性。
多分类问题
-
在之前的分类任务中,二分类问题(0或1)使用Logistic回归即可。对于多分类问题(如猫、狗、小鸡或其他),需要扩展为Softmax回归。Softmax 回归通过为每个类别计算概率,确保概率总和为1,用于解决多分类问题。
假设分类任务有 \(C\) 种可能的类别,那么类别 \(0\) 表示不属于任何一类,类别 \([1,C-1]\) 表示特定的类别。 神经网络的输出层包含 \(C\) 个节点,每个节点的输出表示该类别的概率。输出向量 \(\hat{y}\) 是一个 \(C×1\) 维的向量,其元素表示每个类别的预测概率,所有概率的总和为1。
首先在输出层进行线性变换:
\[z^{[L]} = W^{[L]}a^{[L-1]} + b^{[L]} \]然后对 \(z^{[L]}\) 的每个元素取指数:
\[t_i = e^{z_i^{[L]}} \]随后计算归一化概率向量:
\[a^{[L]} = \frac{t}{\sum_{j=1}^{C} t_j} \\ a_i^{[L]} = \frac{e^{z_i^{[L]}}}{\sum_{j=1}^{C} e^{z_j^{[L]}}} \]最终输出 \(a^{[L]}\) 是经过Softmax变换的概率分布,表示每个类别的预测概率。
Hardmax直接选取最大值位置为1,其它为0,如 \([1 \;0 \;0 \;0]^T\)。Softmax通过概率分布进行平滑转换,更适合梯度下降优化,如 \([0.3\;0.2\;0.1\;0.4]^T\)。
其实Softmax是Logistic回归的多分类扩展,当\(C=2\)时,Softmax退化为Logistic回归。当没有隐藏层时,决策边界是线性分割,每两个类别之间的分界面是线性的。在二维输入空间中,Softmax 分类器可以用几条线性决策边界将空间划分为多个区域,每个区域对应一个类别。有隐藏层时,网络可以学习更复杂的非线性决策边界,从而实现更强大的分类能力。
-
Softmax 将输出层的线性变换结果 \(z^{[L]}\) 转化为概率分布 \(a^{[L]}\) ,输出的 \(a^{[L]}\) 是一个 \(C×1\) 的向量,表示 \(C\) 个类别的概率,且总和为1。
\[ L(\hat{y}, y) = -\sum_{j=1}^C y_j \log(\hat{y}_j) \]
对于单个样本真实标签 \(y=[0\;1\;0\;0]^T\) 和预测概率分布 \(\hat{y}=[0.3\;0.2\;0.1\;0.4]^T\) ,使用交叉熵损失:当真实类别是 \(j\) ,即 \(y_j=1\) 时, \(L = -\log(\hat{y}_j)\)。损失函数的目标是使真实类别的预测概率 \(\hat{y}_j\) 尽可能接近1。对整个训练集,将所有样本的损失求平均:
\[ J(W, b) = \frac{1}{m} \sum_{i=1}^m L(\hat{y}^{(i)}, y^{(i)}) \]其中, \(m\) 是训练样本的数量。
在梯度下降的过程,对 \(J(W, b)\) 求梯度,通过反向传播更新参数。首先计算输出层的误差项:
\[ dz^{[L]} = \hat{y} - y \]\(\hat{y}\) 是模型的预测, \(y\) 是真实标签。 \(dz^{[L]}\) 是损失函数对 \(z^{[L]}\) 的偏导数。利用 \(dz^{[L]}\) 计算其他参数的梯度,并反向传播到隐藏层。大多数深度学习框架(如TensorFlow、PyTorch)会自动处理反向传播。用户只需定义前向传播和损失函数,框架会自动计算梯度。