
大侠幸会,在下全网同名「算法金」 0 基础转 AI 上岸,多个算法赛 Top 「日更万日,让更多人享受智能乐趣」
高斯过程算法是一种强大的非参数机器学习方法,广泛应用于回归、分类和优化等任务中。其核心思想是利用高斯分布来描述数据的分布,通过核函数来度量数据之间的相似性。与传统的机器学习方法相比,高斯过程在处理小样本数据和不确定性估计方面具有独特的优势。
接下来,我们将详细探讨高斯过程的基本原理、数学表述及其在机器学习中的应用,并提供相关的代码示范和实际案例分析。

1. 高斯过程的基本原理
1.1 高斯过程定义
高斯过程是一种用于定义数据分布的概率模型。其核心在于任意数量的随机变量的集合中,每个子集的联合分布都是多元正态分布。通俗来讲,高斯过程是一种“函数的分布”,用来描述函数值在给定输入下的可能取值。
1.2 高斯过程的核心思想
高斯过程通过核函数来度量数据点之间的相似性。核函数不仅决定了数据点之间的相互关系,还影响了整个高斯过程模型的平滑性和复杂性。常用的核函数包括线性核、径向基核(RBF核)和多项式核。
1.3 高斯过程与正态分布的关系
高斯过程是由多元正态分布推广而来的。在高斯过程中,每个数据点都可以看作是一个多元正态分布的一部分,其均值和协方差由核函数决定。因此,高斯过程具有与正态分布相同的优良性质,如平稳性和解析性。
更多分布见微*公号往期文章:数据科学家 95% 时间都在使用的 10 大基本分布
95% 数据科学家都在使用,确定数据分布正态性 10 大方法,附 Python 代码
1.4 高斯过程的优点
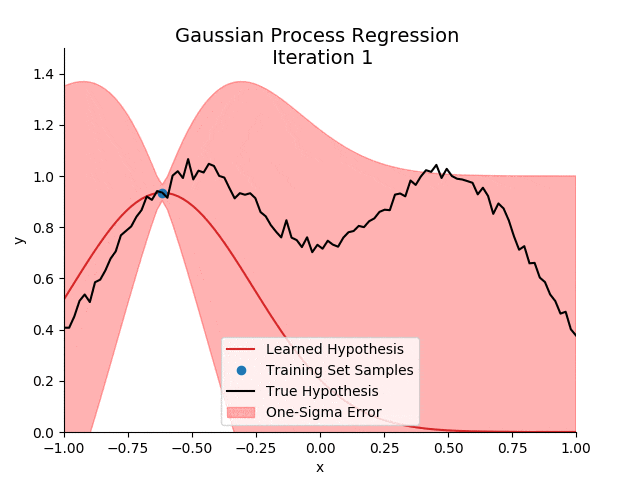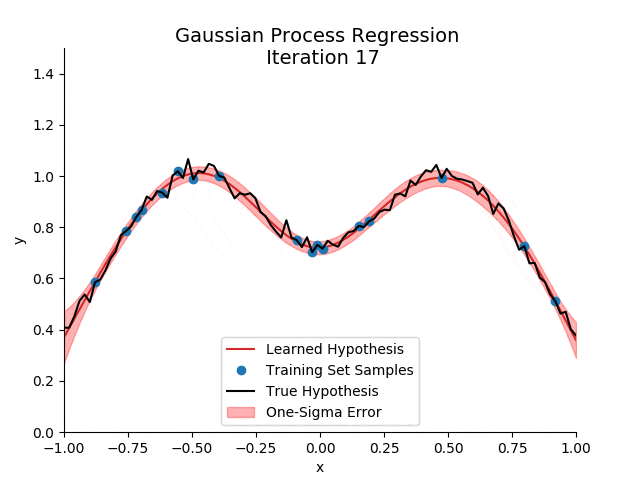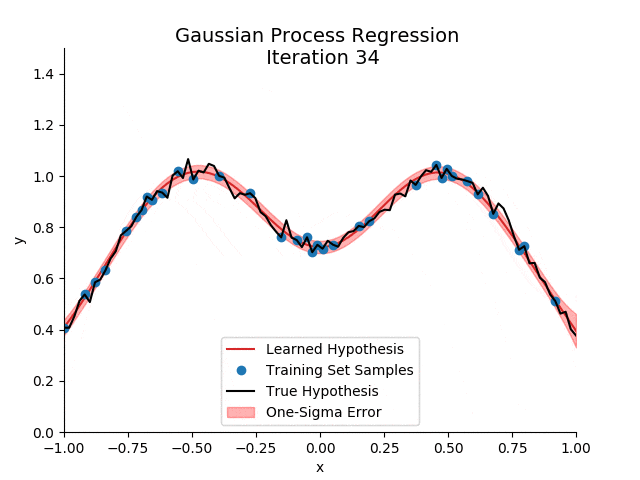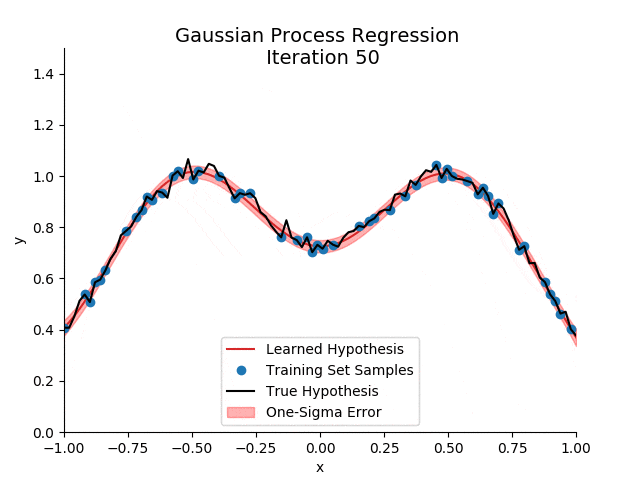
高斯过程在处理小样本数据和不确定性估计方面具有独特的优势:
- 不确定性估计:高斯过程能够自然地给出预测的不确定性。
- 非参数特性:不需要预设数据的分布形式,灵活应对各种数据特征。
- 处理小样本数据:在样本较少的情况下,高斯过程仍能提供准确的预测。
2. 高斯过程的数学表述
不想脑瓜疼的铁子,可以考虑跳过这一部分
2.1 核函数的定义与作用
在高斯过程模型中,核函数(或称为协方差函数)是关键组成部分。它用于度量数据点之间的相似性。常见的核函数包括:
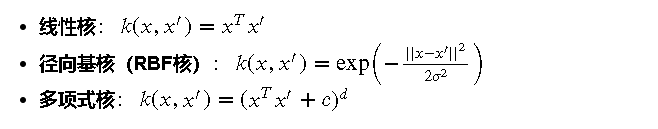
核函数的选择对高斯过程的性能有显著影响,不同的核函数能够捕捉数据的不同特性。
2.2 协方差函数
协方差函数
标签:高斯,GP,过程,模型,胜率,算法,数据,函数 From: https://www.cnblogs.com/suanfajin/p/18246943