圆方树大概分两种,一个是圆方树,一个是广义圆方树。
圆方树
这可以解决仙人掌上的问题。
任意一条边至多只出现在一条简单回路的无向连通图称为仙人掌。
很多题解将其作为无向图构建,本文将其构建为外向树,在这个问题中两种构建方式不会影响求解。
构建方式
记读入的图为原图,构建的圆方树为新图。
首先,新图保留着原图的点集,这些点记为圆点。
将原图任意一个点(实现中指定 \(1\) 号点即可)作为根节点,然后在原图跑一遍 dfs。
每当找到一个环的时候,将进入环的点(也就是边双的根节点)记为头节点,然后在新图上对加一个方点,并让头节点向这个方点连边,边权为 \(0\),同时,方点向其它点 \(u\) 连边,边权为原图中的 \(u\) 到头节点的最短距离。
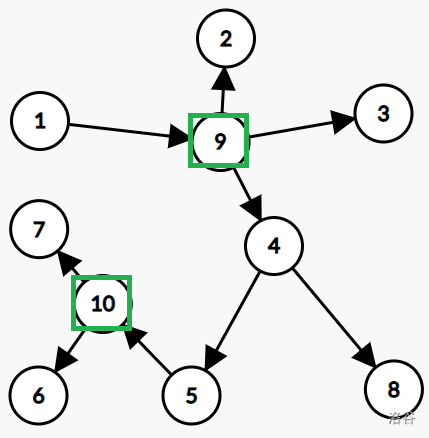
下面使原图与对应新图(圆方树)的一个例子: