
大侠幸会,在下全网同名「算法金」 0 基础转 AI 上岸,多个算法赛 Top 「日更万日,让更多人享受智能乐趣」
1. 引言
今天我们唠唠 吴恩达:机器学习的六个核心算法! 之决策树算法。
决策树是一种用于分类和回归的机器学习算法。它通过一系列的决策规则将数据逐步划分,最终形成一个类似于树状结构的模型。
决策树因其直观、易于解释和高效的特点,被广泛应用于分类和回归问题中。它可以处理连续和离散的数据,并且能够处理多种类型的特征,因而在医学诊断、市场分析、金融预测等领域得到了广泛的应用。
必 须 拿 下 !!!

2. 决策树的基本概念
2.1 什么是决策树
决策树是一种树形结构的模型,它通过一系列的决策规则将数据逐步划分,从而实现分类或回归的目的。决策树由节点和分支组成,根节点代表整个数据集,每个内部节点代表一个特征,每个分支代表一个决策规则,每个叶子节点表示一个最终的预测结果。
决策树算法最早可以追溯到 20 世纪 60 年代。1975 年,J. Ross Quinlan 提出了 ID3 算法,随后又发展出了 C4.5 和 C5.0 算法。1993 年,Leo Breiman 等人提出了 CART(Classification and Regression Trees)算法,这些算法奠定了现代决策树的基础。

(假设一个相亲决策树,By 三点水)

(另一颗相亲决策树,人类的疑惑行为)
2.2 决策树的基本结构
- 根节点(Root Node): 决策树的起始点,包含所有数据。
- 内部节点(Internal Node): 通过特征划分数据的节点,每个节点代表一个特征。
- 分支(Branch): 从节点分裂出来的路径,表示特征的不同取值。
- 叶子节点(Leaf Node): 最终的分类或回归结果。

2.3 决策树的工作原理
决策树通过递归地选择最优特征来划分数据。具体步骤如下:
- 特征选择: 在当前节点选择能够最好地划分数据的特征。
- 数据划分: 根据选择的特征将数据划分成子集。
- 递归构建: 对每个子集重复上述过程,直到满足停止条件(如节点纯度达到一定水平或节点包含的样本数过少)。
2.4 决策树的优缺点
优点:
- 直观易懂,易于解释。
- 处理分类和回归问题。
- 适用于处理数值型和类别型特征。
缺点:
- 容易过拟合,尤其是深度较大的树。
- 对于类别较多的特征,信息增益偏向于取值多的特征。
- 对数据中的噪声和异常值较敏感。
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
import numpy as np
# 生成武侠风格的数据,确保所有特征值为正数
X, y = make_classification(n_samples=200, n_features=2, n_redundant=0, n_informative=2,
n_clusters_per_class=1, random_state=42)
X += np.abs(X.min()) # 平移数据确保为正
# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 创建决策树模型,并设置最大深度为3
dt = DecisionTreeClassifier(max_depth=3)
# 训练模型
dt.fit(X_train, y_train)
# 绘制数据点和决策边界
def plot_decision_boundary(model, X, y):
# 设置最小和最大值,以及增量
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),
np.arange(y_min, y_max, 0.01))
# 预测整个网格的值
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 绘制决策边界
plt.contourf(xx, yy, Z, alpha=0.4)
# 绘制不同类别的样本点
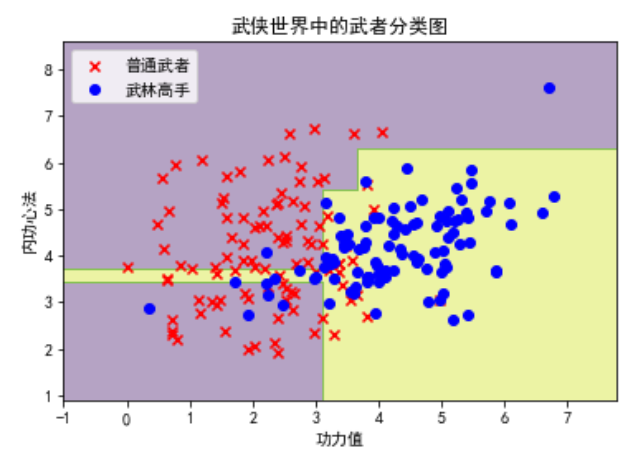
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], c='red', marker='x', label='普通武者')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], c='blue', marker='o', label='武林高手')
plt.xlabel('功力值')
plt.ylabel('内功心法')
plt.title('武侠世界中的武者分类图')
plt.legend()
# 绘制决策边界和数据点
plot_decision_boundary(dt, X, y)
plt.show()

3. 决策树的构建
3.1 特征选择
特征选择是决策树构建的关键步骤。常用的特征选择标准包括信息增益、增益比和基尼指数。
- 信息增益(Information Gain): 衡量特征对数据集信息熵的减少程度,信息增益越大,特征的区分能力越强。
- 增益比(Gain Ratio): 是对信息增益的改进,考虑了特征的取值数目。
- 基尼指数(Gini Index): 衡量数据集的不纯度,基尼指数越小,数据集越纯。
3.2 树的分裂准则
分裂准则决定了如何在每个节点处划分数据。不同的决策树算法使用不同的分裂准则:
- ID3算法: 使用信息增益作为分裂准则。
- C4.5算法: 使用增益比作为分裂准则。
- CART算法: 使用基尼指数作为分裂准则。
3.3 树的生长和剪枝
- 树的生长: 决策树从根节点开始,不断选择最优特征进行分裂,直到所有叶子节点都达到纯度或满足停止条件。
- 剪枝: 为了防止过拟合,可以对决策树进行剪枝。剪枝分为预剪枝和后剪枝。预剪枝是在树生长过程中停止分裂,后剪枝是在树完全生长后去掉一些叶子节点。
示例代码
下面是一个详细展示如何构建和优化决策树的例子。
import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeClassifier, export_text
from sklearn.model_selection import train_test_split
from sklearn import metrics
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
# 构造武侠元素数据集
data = {
'武功': ['高', '中', '低', '高', '中', '低', '高', '中'],
'轻功': ['强', '强', '弱', '弱', '强', '强', '弱', '弱'],
'身份': ['正派', '邪派', '正派', '邪派', '正派', '邪派', '正派', '邪派'],
'是否获胜': ['是', '是', '否', '否', '是', '否', '是', '否']
}
# 转换为DataFrame
df = pd.DataFrame(data)
# 特征和标签
X = pd.get_dummies(df.drop('是否获胜', axis=1))
y = df['是否获胜'].apply(lambda x: 1 if x == '是' else 0)
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 创建决策树分类器
clf = DecisionTreeClassifier(criterion='entropy', max_depth=3)
clf = clf.fit(X_train, y_train)
# 预测
y_pred = clf.predict(X_test)
# 模型评估
print("准确率:", metrics.accuracy_score(y_test, y_pred))
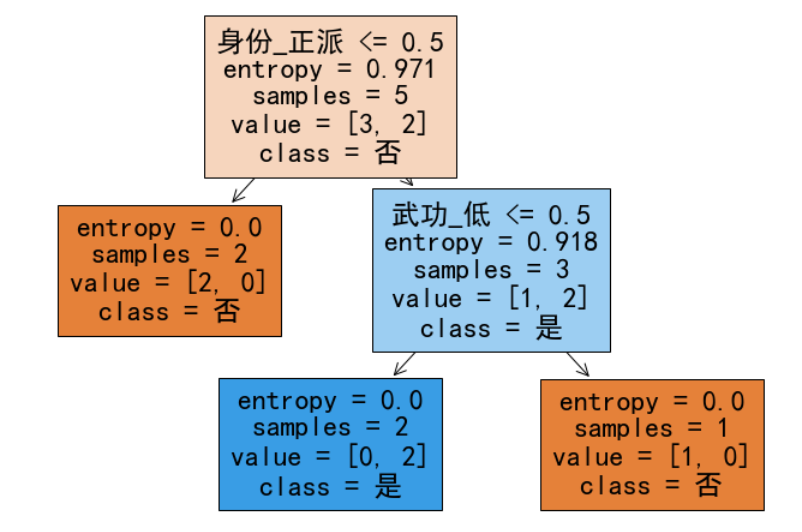
# 决策树可视化
plt.figure(figsize=(12, 8))
plot_tree(clf, filled=True, feature_names=X.columns, class_names=['否', '是'])
plt.show()
# 显示决策树的规则
tree_rules = export_text(clf, feature_names=list(X.columns))
print(tree_rules)


4. 决策树的算法实现
4.1 ID3算法
ID3算法(Iterative Dichotomiser 3)是由 J. Ross Quinlan 在 1986 年提出的一种决策树算法。它使用信息增益作为特征选择的标准,递归地构建决策树。
信息熵(Entropy)表示数据集的纯度,计算公式为:

ID3算法的步骤
- 计算当前特征的信息增益。
- 选择信息增益最大的特征进行数据划分。
- 对每个子集递归地调用上述过程,直到所有数据属于同一类别或没有更多特征可供选择。
示例代码
from sklearn.tree import DecisionTreeClassifier, export_text
from sklearn.model_selection import train_test_split
from sklearn import metrics
# 使用 ID3 算法
clf_id3 = DecisionTreeClassifier(criterion='entropy')
clf_id3 = clf_id3.fit(X_train, y_train)
# 预测
y_pred_id3 = clf_id3.predict(X_test)
# 模型评估
print("ID3 准确率:", metrics.accuracy_score(y_test, y_pred_id3))
# 显示决策树的规则
tree_rules_id3 = export_text(clf_id3, feature_names=list(X.columns))
print(tree_rules_id3)
4.2 C4.5算法
C4.5算法是对ID3算法的改进,主要改进点在于使用增益比(Gain Ratio)来进行特征选择,克服了信息增益偏向于多值特征的问题。
C4.5算法的步骤
- 计算当前特征的信息增益比。
- 选择信息增益比最大的特征进行数据划分。
- 对每个子集递归地调用上述过程,直到所有数据属于同一类别或没有更多特征可供选择。
4.3 CART算法
CART算法(Classification and Regression Trees)由 Leo Breiman 等人在 1984 年提出,它使用基尼指数作为特征选择标准。CART 算法可以用于分类和回归任务。计算公式为:

CART算法的步骤
- 计算当前特征的基尼指数。
- 选择基尼指数最小的特征进行数据划分。
- 对每个子集递归地调用上述过程,直到所有数据属于同一类别或没有更多特征可供选择。
示例代码
# 使用 CART 算法
clf_cart = DecisionTreeClassifier(criterion='gini')
4.4 决策树的可视化
决策树的可视化可以帮助我们更直观地理解模型的决策过程。
示例代码
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
# 可视化 ID3 决策树
plt.figure(figsize=(12, 8))
plot_tree(clf_id3, filled=True, feature_names=X.columns, class_names=['否', '是'])
plt.title("ID3 决策树")
plt.show()
# 可视化 CART 决策树
plt.figure(figsize=(12, 8))
plot_tree(clf_cart, filled=True, feature_names=X.columns, class_names=['否', '是'])
plt.title("CART 决策树")
plt.show()
通过上述代码,我们可以构建不同的决策树模型,并对其进行可视化和评估。
决策树的可视化除了使用 scikit-learn 自带的 plot_tree 方法之外,还有其他专门的库可以用于更加专业和美观的可视化。以下是几个常用的方法和库:
- 使用 Graphviz 和 pydotplus
Graphviz 是一个开源的图形可视化软件,可以用来生成决策树的图像。配合 pydotplus 库,可以很方便地将 scikit-learn 的决策树模型转换为 Graphviz 的格式并进行可视化。
pip install graphviz pydotplus
from sklearn.tree import export_graphviz
import pydotplus
from IPython.display import Image
# 导出决策树为 DOT 格式的数据
dot_data = export_graphviz(clf, out_file=None,
feature_names=X.columns,
class_names=['否', '是'],
filled=True, rounded=True,
special_characters=True)
# 使用 pydotplus 将 DOT 数据转换为图像
graph = pydotplus.graph_from_dot_data(dot_data)
Image(graph.create_png())
- 使用 dtreeviz
dtreeviz 是一个专门用于决策树可视化的库,可以生成非常美观和详细的决策树图。
pip install dtreeviz
from dtreeviz.trees import dtreeviz
# 使用 dtreeviz 可视化决策树
viz = dtreeviz(clf, X_train, y_train,
target_name='是否获胜',
feature_names=X.columns,
class_names=['否', '是'])
# 展示决策树
viz.view()
- 使用 plotly 和 dash
plotly 和 dash 是强大的可视化库,可以用来创建交互式的决策树图表。
pip install plotly dash
import plotly.graph_objs as go
from dash import Dash, dcc, html
# 创建决策树图表
fig = go.Figure(go.Sunburst(
labels=["根节点", "节点1", "节点2", "节点3", "节点4"],
parents=["", "根节点", "根节点", "节点1", "节点1"],
values=[1, 2, 3, 4, 5],
))
# 创建 Dash 应用
app = Dash(__name__)
app.layout = html.Div([
dcc.Graph(id='tree', figure=fig)
])
if __name__ == '__main__':
app.run_server(debug=True)
- 使用 yellowbrick
yellowbrick 是一个用于模型可视化的库,可以方便地可视化决策树。
pip install yellowbrick
from yellowbrick.model_selection import ValidationCurve
from sklearn.tree import DecisionTreeClassifier
# 创建决策树分类器
model = DecisionTreeClassifier()
# 使用 ValidationCurve 可视化决策树
viz = ValidationCurve(
model, param_name="max_depth",
param_range=np.arange(1, 11), cv=10, scoring="accuracy"
)
viz.fit(X_train, y_train)
viz.show()
这些方法和库提供了丰富的可视化选项,可以根据需要选择适合的工具进行决策树的可视化。

5. 决策树的优化
5.1 特征选择的重要性
特征选择是构建高效决策树的关键步骤。选择合适的特征不仅可以提高模型的准确性,还可以减少模型的复杂度,避免过拟合。
特征选择的主要方法包括:
- 过滤法:使用统计方法选择特征,如方差分析、卡方检验等。
- 包裹法:使用机器学习算法评估特征,如递归特征消除(RFE)。
- 嵌入法:在模型训练过程中选择特征,如决策树的特征重要性。
示例代码
from sklearn.feature_selection import SelectKBest, chi2
# 使用卡方检验选择最佳特征
X_new = SelectKBest(chi2, k=2).fit_transform(X, y)
5.2 剪枝技术的应用
剪枝技术用于防止决策树过拟合。主要包括预剪枝和后剪枝:
- 预剪枝:在树的构建过程中提前停止,如限制树的深度。
- 后剪枝:先构建完整的树,再去除不必要的节点。
示例代码
# 预剪枝:限制最大深度
clf_preprune = DecisionTreeClassifier(max_depth=3)
clf_preprune.fit(X_train, y_train)
# 后剪枝:使用 cost complexity pruning
path = clf_preprune.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas = path.ccp_alphas
# 选择最佳的 alpha 值进行剪枝
clf_postprune = DecisionTreeClassifier(ccp_alpha=ccp_alphas[-1])
clf_postprune.fit(X_train, y_train)
5.3 集成方法:随机森林
随机森林通过构建多棵决策树并将它们的结果进行投票,来提高模型的泛化能力和准确性。
示例代码
from sklearn.ensemble import RandomForestClassifier
# 创建随机森林分类器
clf_rf = RandomForestClassifier(n_estimators=100)
clf_rf.fit(X_train, y_train)
# 预测
y_pred_rf = clf_rf.predict(X_test)
# 模型评估
print("随机森林准确率:", metrics.accuracy_score(y_test, y_pred_rf))
5.4 集成方法:梯度提升树
梯度提升树通过逐步构建决策树,每棵新树都是为了纠正前一棵树的误差,从而提高模型的准确性。
示例代码
from sklearn.ensemble import GradientBoostingClassifier
# 创建梯度提升分类器
clf_gb = GradientBoostingClassifier(n_estimators=100)
clf_gb.fit(X_train, y_train)
# 预测
y_pred_gb = clf_gb.predict(X_test)
# 模型评估
print("梯度提升树准确率:", metrics.accuracy_score(y_test, y_pred_gb))

6. 决策树的变体
6.1 随机森林
随机森林(Random Forest)是一种集成学习方法,通过构建多个决策树并将它们的预测结果进行投票或平均,来提高模型的准确性和稳定性。每棵树在训练时使用了不同的子集和特征子集,这种随机性使得随机森林对噪声和过拟合有较强的抵抗能力。
具体的,可以留言,想看的读者多的话,专门开一篇详细展开
6.2 极端随机树
极端随机树(Extra Trees 或 Extremely Randomized Trees)是另一种集成方法,与随机森林类似,但在构建每棵树时,它对特征的选择和分割点的选择更加随机。这种极端随机化减少了方差,但可能会增加偏差,使得模型更加简单和快速。
6.3 梯度提升树
梯度提升树(Gradient Boosting Trees)是一种提升方法,通过逐步构建一系列的决策树,每棵新树都是为了纠正前一棵树的错误。它通过逐步优化损失函数,使得模型的预测结果越来越好。梯度提升树在处理回归和分类问题时表现出色,特别是在处理复杂数据集时。
6.4 XGBoost
XGBoost(Extreme Gradient Boosting)是一种高效的梯度提升实现,具有很高的计算效率和预测性能。XGBoost 引入了正则化项以防止过拟合,并通过使用分布式计算加速训练过程。它在许多机器学习竞赛中表现优异,成为数据科学家的常用工具。
还有 CatBoost,LGB
具体的,可以留言,想看的读者多的话,专门详细展开,这个可以写好几篇
[ 抱个拳,总个结 ]
决策树是一种简单而强大的机器学习算法,广泛应用于分类和回归问题,必须拿下。通过优化特征选择、应用剪枝技术和使用集成方法,可以进一步提高决策树的性能。在实际应用中,掌握决策树的常见问题及解决方法,对于构建高效、稳定的模型至关重要。

[ 算法金,碎碎念 ]
全网同名,日更万日,让更多人享受智能乐趣
烦请大侠多多 分享、在看、点赞,助力算法金又猛又持久、很黄很 BL 的日更下去;
同时邀请大侠 关注、星标 算法金,围观日更万日,助你功力大增、笑傲江湖
标签:clf,算法,train,最强,import,节点,决策树 From: https://www.cnblogs.com/suanfajin/p/18224065