数据结构与算法
#自定义比较器
#1. 对list等有key参数的
##二维数组等的比较排序
list1.sort(key = lambda x: x[1])
##list中放置其他数据类型
import functools
#cmp的返回值为负数,第一个数在第二个数前面
#cmp的返回值为正数,第二个数在第一个数前面
def cmp(s1, s2):
pass
list1.sort(key = functools.cmp_to_key(cmp))
#2. 队列操作
import queue
q = queue.Queue()
q.put()
q.get()
#3.优先级队列
qp = queue.Priorityqueue()
qp.put()#通常为一个(2,)的数据,第一位为优先级,越小越优先,第二位为放入的数据项
#4.堆的操作
import heapq
heap = []
heapq.heappush(heap, list_data)#第一种把heap初始化为小根堆
heapq.heapify(list_data)#第二种
heapq.heappop(0)#弹出根节点
四大逻辑结构:集合结构,线性结构,树形结构,图形结构
物理结构:顺序存储(地址连续), 链式存储(更灵活)
算法效率
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2)
1. 排序
选择排序
思想: 依次找到最小值放到最前面 时间复杂度O(n^2),空间复杂度O(1)
//(0 ----N-1)位置找到min放到0位置
//(1------N-1) 位置找到min放到1位置
冒泡排序
思想:(0 ---N-1)相邻两个比较,max往右移动;(0--N-2)相邻两个比较,max右移
// 1 2 3 4 5 6
// 1 2 位置谁大谁往右移
// 2 3 位置上谁大谁往右移
// 3 4 位置上谁大谁往右移
插入排序
思想:保证0-1有序,保证0-2有序,保证0-3有序,如果i位置比i-1位置小,交换,直到i不比i-1位置小。
def xuanze(arr):#选择排序
for i in range(len(arr)):
for j in range(i+1, len(arr)):
# print(i)
if arr[j] < arr[i]:
arr[i], arr[j] = arr[j],arr[i]
return arr
def maopao(arr):#冒泡排序
for i in range(len(arr)):
for j in range(len(arr) -1-i):
if arr[j] > arr[j+1]:
arr[j+1], arr[j] = arr[j], arr[j+1]
return arr
def charu(arr):#插入排序
for i in range(1, len(arr)):
now = i
for j in range(i-1, -1, -1):
global bigo
bigo += 1
if arr[now] < arr[j]:
print(str(now)+'位置换到'+str(j)+'位置去')
arr[now], ar r[j] = arr[j], arr[now]
now = j
else:
break
global bigo#用于查看到底进行了几次
bigo = 0
arr = [1,2,3,4,6,0]
print(arr)
charu(arr)
print(arr)
print(bigo)
二分(logn)
递归做
arr = [1,2,3,4,5,6]
def erfeng(arr, num, L, R):
print('again')
if L == R:
pass
mid = int(L +(R-L)/2)
if num < arr[mid]:
R = mid
erfeng(arr, num, L, R)
elif num > arr[mid]:
L = mid +1
erfeng(arr,num, L,R)
else:
print('zhaodaol')
print(arr[mid])
L = 0
R = len(arr)
erfeng(arr, 1, L, R)
有序数列找比x小的最左侧数
arr = [1,1,1,1,1,1,1,2,2,2,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,5,5,6,6,6,6,6,6,6,6,6]
def erfengzuo(arr, num, L, R, t):#first, t = R
print('now is %d, %d'%(L, R))
mid = int(L + (R - L)/2)
if arr[mid] >= num:
if L == mid:
raise IndexError
if t> mid:
t = mid
R = mid
erfengzuo(arr, num, L, R, t)
elif arr[mid]< num:
L = mid +1
erfengzuo(arr, num, L, R, t)
else:
print(arr[mid])
erfengzuo(arr, 3,0, len(arr), len(arr))
还有 无序数组上找局部最小的问题(画出来,思维很简单)
对数器 可以提供类似OJ的效果
random() [0,1) 等概率返回一个小数
int(random()*N) 等概率返回一个[0, N) 上的随机整数
快速排序(荷兰国旗问题)
给定数组arr, 和一个数num,把小于num的数放在数组左边,大于num的数放在数组右边,时间复杂度为O(n),空间复杂度为O(1).
升级: 一个数组,左边小于num, 中间== num, 右边大于num
思维误区:三个指针, 小于区的右边界,等于区的右边界*** 等于区的右边界其实是大于区的左边界***
时间复杂度O(N * logn), 空间复杂度O(logn)
import random
def kuaisu(arr, L, R):
if L< R: #注意判断条件!!!使用(2,2,3)试一试
random_num = int(random.random()*(len(arr)-1))#转化为int类型!!!
print('前arr%s'% arr)
num = arr[random_num]
print('num: arr的第%d 个数,num为%d' % (random_num, num))
small, big = equalok(arr,num,L, R)
print('small:%d; big:%d'% (small, big))
print('L :%d; R :%d'%(L, R))
print('后arr%s'% arr)
kuaisu(arr, L, small)
kuaisu(arr, big, R)
def equalok(arr, num, L, R):
small = L-1#注意边界问题i的取值是L开始的
big = R +1
i = L
while(i != big):
if arr[i]< num:
arr[i], arr[small +1] = arr[small +1], arr[i]
i += 1
small += 1
elif arr[i]> num:
arr[i], arr[big -1] = arr[big-1], arr[i]
big -= 1
elif arr[i] == num:
i +=1
return small, big
arr = [1,23,3,4,2]
kuaisu(arr, 0, len(arr)-1)
print(arr)
2. 递归
master公式 T(N) = a* T(N/b) + o(N^d)
while : a 子问题调用次数, N/b 子问题规模, o(N^d) 处理递归外的其他复杂度
log(b,a)< d 为O(N^d)
log(b, a) > d 为 O(N^(log(a,b)))
log(b, a) = d 为O( N^d * logn)
归并排序
经典问题
时间复杂度 : O(N * logN)
注意点:如果a = [0,1], mid = 0, 打印a[L, mid] 结果为None
def merge(arr, L, R):
if L+1 == R:
print(L, end = ' ')
print(R)
if arr[L] > arr[R]:
arr[L], arr[R] = arr[R], arr[L]
return arr
elif L ==R:#注意对只有1个和2个元素时的处理方式
return arr
else:
mid = int(L + (R-L)/2)#mid一定要转为整形
merge(arr, L, mid)
merge(arr, mid +1, R)
arr[L: R+1] = togother(arr, L, R, mid)
return arr
def togother(arr, L, R, mid):
p1 = L
p2 = mid+1
help1 = []
while( p1< mid +1 and p2 < R +1):#注意剩余几个元素的拉去条件
if arr[p1]< arr[p2]:
help1.append(arr[p1])
p1 += 1
else:
help1.append(arr[p2])
p2 += 1
if p1 == mid+1 :
help1.extend(list(arr[p2:R+1]))
if p2 == R+1:
help1.extend(list(arr[p1:mid+1]))
return help1
arr = [1,3,6,4,9,4,0,23,3]
arr = merge(arr, 0, len(arr)-1)
print(arr)
求小和问题
( 1,3,4,2,5)求每个数左边比这个数小的和
:在一个数组中,每一个数左边比当前数小的数累加起来,叫做这个数组的小和
注意点:思维转化,把比某个数左边小的数总和,变为某个数右边有多少个比它大的
逆序对问题:在一个数组中,左边的数如果比右边的数大,则这两个数构成一个逆序对。求所有的逆序对。
思维同样转换为上述。
小和问题代码:
#1.134和25合并时,左边的小和已经计算过了,所以只需要管右边的就可以
# 某个数不会和自己所在的组产生小和;
#2. 当左右数据相同时,先把右边的merge进去。
global he
he = 0
def xiaohe(arr, L, R):
if L + 1 == R:
if arr[L]> arr[R]:
arr[L], arr[R] = arr[R], arr[L]
elif arr[L] == arr[R]:
pass
else:
global he
he += arr[L]
print('two merge:%d'% he)
return arr
elif L == R:
return arr
else:
mid = int(L + (R-L)>>1)
xiaohe(arr, L, mid)
xiaohe(arr, mid+1, R)
print('left : %s'% arr[L:mid+1], end = ' ')
print('right: %s'% arr[mid+1: R+1])
arr[L:R+1] = togother(arr, L, mid, R)
print('merge: %s' % arr[L:R+1])
return arr
def togother(arr, L, mid,R):
p1 = L
p2 = mid+1
help1 = []
while(p1<mid+1 and p2< R+1):
if arr[p1]<arr[p2]:
help1.append(arr[p1])
global he
he += (arr[p1] * (R - p2+1))
print('p1: %d, p2:%d, 乘数:%d'%(p1, p2, (R-p2 +1)))
print('all merge: %d'% he)
p1 +=1
else: #if arr[p1]>=arr[p2]:
help1.append(arr[p2])
p2 += 1
while(p1 == mid +1) :
help1.extend(list(arr[p2:R+1]))
p1 += 1
print('?')
while(p2 == R +1):
help1.extend(list(arr[p1: mid +1]))
p2 += 1
print('?')
return help1
arr = [1,3,4,2,5]
arr = xiaohe(arr, 0, len(arr)-1)
print(he)
print(arr)
3. 堆
堆结构就是用数组实现的完全二叉树结构,堆中的某个节点总是不小于或不大于其父节点的值。
一个数组从0开始,连续的一段可以构成完全二叉树
特性 :1.连续的长度用size表示
- i位置的左孩子为: 2 * i +1; i 位置的右孩子为 2 * i + 2;当 这个值比size小时;
- i 位置的父节点为: int((i -1)/ 2 ) # 包括0节点
大根堆:完全二叉树中,如果每棵子树的最大值都在顶部;小根堆:完全二叉树的每棵子树的最小值都在顶部
heapinsert操作和 heapify操作,以及堆排序
堆排序思想:
- 把数组arr变成一个堆
- 把跟节点和最后一个数交换,pop出来,heapsize --, 直到heapsize = 0.
时间复杂度: [........|........],如果有2N个元素,后面N个排序最差需要logN次, 共N个,所以是N*(logn)
#堆排序和两个操作
def heapinsert(arr, index):
while(arr[index]> arr[int((index -1)/2)]):
arr[index], arr[int((index - 1)/2)] = arr[int((index -1)/2)], arr[index]
index = int((index -1)/2)
def heapify(arr, index, heapsize):
left = 2 * index + 1
while(left < heapsize):
max_num = left+1 if left+1 < heapsize and arr[left + 1] > arr[left] else left
max_num = max_num if arr[index] < arr[max_num] else index
if (max_num == index):
break
arr[index], arr[max_num] = arr[max_num], arr[index]
index = max_num
left = 2 * index +1
def heapsort(arr):
for i in range(len(arr)-1):
heapinsert(arr, i)
print(arr)
heapsize = len(arr)
arr[0], arr[len(arr) - 1] = arr[len(arr) - 1], arr[0]
heapsize -=1
heapify(arr, 0, heapsize)
while(heapsize > 0):
arr[0], arr[heapsize - 1] = arr[heapsize - 1], arr[0]
heapsize -= 1
heapify(arr, 0, heapsize)
arr = [1,3,2,6,5,8,3,5]
heapsort(arr)
print(arr)
扩展
已知一个几乎有序的数组,(每个元素的移动距离不超过k)选择
import heapq#直接使用以及有的库,库默认为小根堆
def distancelessk(arr, k):
heap = []
for i in range(k+1):
heapq.heappush(heap, arr[i])
index = 0
while(index+k +1 < len(arr)):
arr[index] = heapq.heappop(heap)
heapq.heappush(heap, arr[index+k + 1])
index += 1
for i in range(k+1):
arr[index] = heapq.heappop(heap)
#print(arr[index])
index += 1
arr= [2,3,1,5,6,4,7,9,8]
distancelessk(arr, 2)
print(arr)
heapq中 大根堆的实现:heappush()的时候,填入数据*-1, heappop()的时候, 出来的数据 * -1
比较器
比较器的实质就是重载比较运算符
自定义比较器返回值为负数, 第一个参数在前面
返回值为正数,第二个数排前面(升序排列)自己修改
在sort函数中添加排序的策略,可以实现自己的比较器
之前的排序都是基于两个数的比较进行的
不基于比较的排序:只有很窄的应用范围,
4. 桶排序
不基于比较的排序,有条件限制
记数排序
eg_-1: 员工年龄排序,构建一个[16, ....., 100]的数组,遇到某个岁数,某个岁数++,遍历一遍后,得到员工年龄词频统计表, 得到排序。
基数排序[17, 13, 25, 100, 72]
补全最高位的0, 按照最后一位数字进桶(桶是队列,先进先出)
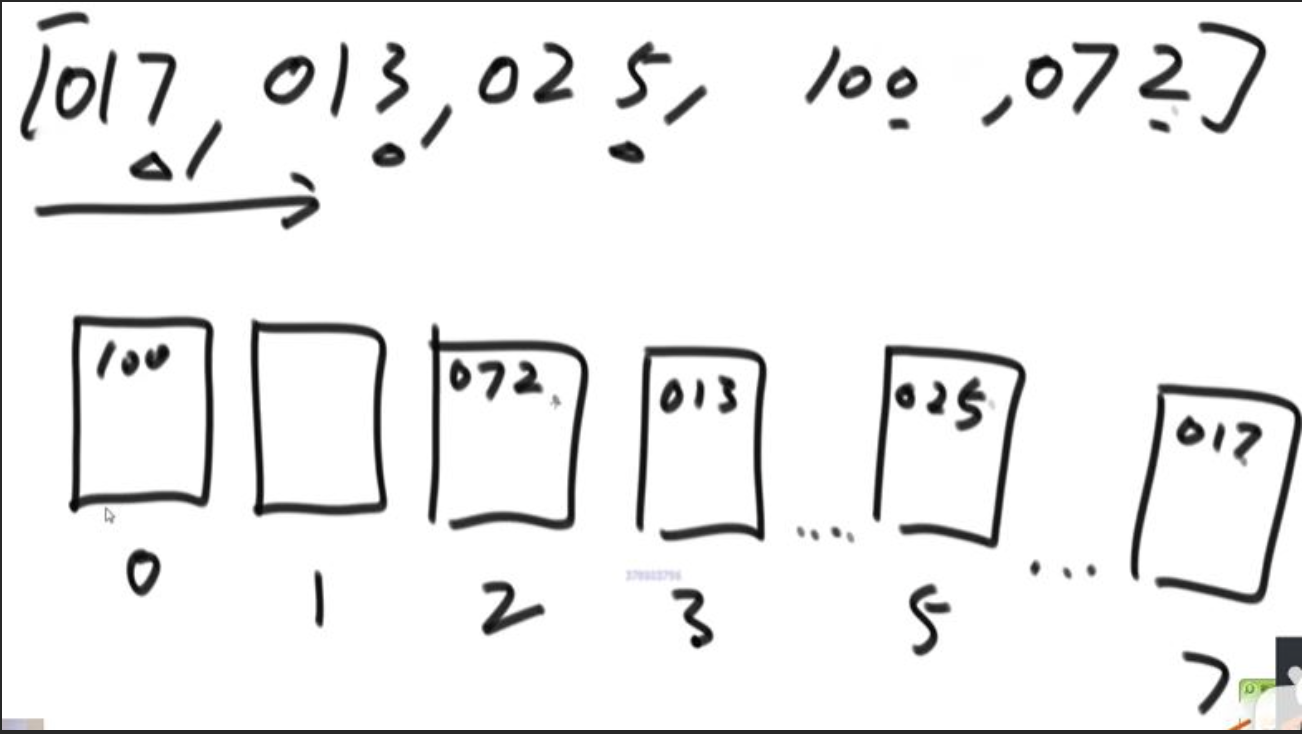
导出桶中数字:
[100, 072, 013, 025, 017]
按照第二位进桶
0: 100,
1:013, 017
2:025
7:072
出桶: [100, 013, 017, 025 ,072]
按照第三位进桶:
0:013, 017, 024, 072
1: 100
出桶: [13, 17, 24, 7, 100]
5. 排序算法汇总
排序稳定性: 指相同的元素再每次排序后是否能保持相同的位置(相同元素的相对次序)
eg: arr1[]:对商品价格从小到大排序
arr2[]: 基于上述排序对好评率从小到大排序,若能保持上述数据的排序基础,则很有价值(体现排序的稳定性)
6个排序稳定性: 堆排,快排

快排最常用(常数项最低,所以最快一般),有空间要求选堆排,有稳定性要求选归并
- 基于比较的时间复杂度最低N*logn
- 时间复杂度最低,空间复杂度小于N,则不能实现稳定性
排序的改进:
- 大规模时候采用N*logn的排序调度算法,小范围用N^2的算法比较快
- 稳定性考虑
6. 哈希
- 如果只有Key,没有value,使用Hashset结构;key-value对,用hashmap结构
- 哈希操作复杂度为常数项,但常数比较大。
- key值为基础类型(int,string...),则直接复制;key值为自定义类型(类),则为自定义类型的内存地址
7. 链表
题目:
-
单链表双链表 反转(换头带返 回值,否则不带)
-
打印两个有序链表的公共部分,给定两个有序链表的头指针h1,h2;
技巧: 1. 使用额外数据记录结构(哈希表);2. 快慢指针
-
判断链表是否为回文结构(前后对称):遍历进栈,pop的时候和原链表比较
-
给定一个单链表head,整数类型,给一个数pivot,将链表调整为做部分小于pivot,中间等于,右边小于。
-
复制含有随机指针节点的链表
-
两个链表相交问题:给定两个可能有环也可能无环的单链表,头节点head1,head2,实现一个函数,如果两个链表相交,返回相交的第一个节点,如果不相交,返回null
8. 二叉树
class Node:
V value
Node left
Node right
-
用递归和非递归两种方式实现二叉树的先序、中序、后序遍历,
-
直观的打印二叉树
-
完成二叉树的宽度优先遍历(求一颗二叉树的宽度)
递归序:
递归的核心代码:
def recur(Node):
if (Node == None):
return
#第一次到该节点的操作代码
recur(Node.left)
#第二次回到该节点所执行的代码
recur(Node.right)
#第三次回到该节点所执行的代码
要点 : 递归

递归序的基础上,可以加工出先序、中序、后序。(顺序是对于每个子树都是这样)
先序(头,左,右): 打印头节点,打印左节点,打印右节点(在递归算法中第一次打印)
中序(左,头,右):4,2,5,1,6,3,7(在递归算法中第二次打印,第一次和第三次都不打印)
后序(左,右,头):4, 5,2,6,7,3,1(在递归算法中第三次打印,第一次和第二次都不打印)
非递归序
任何递归都可以改成非递归函数
自己准备一个栈
先序遍历

后续遍历
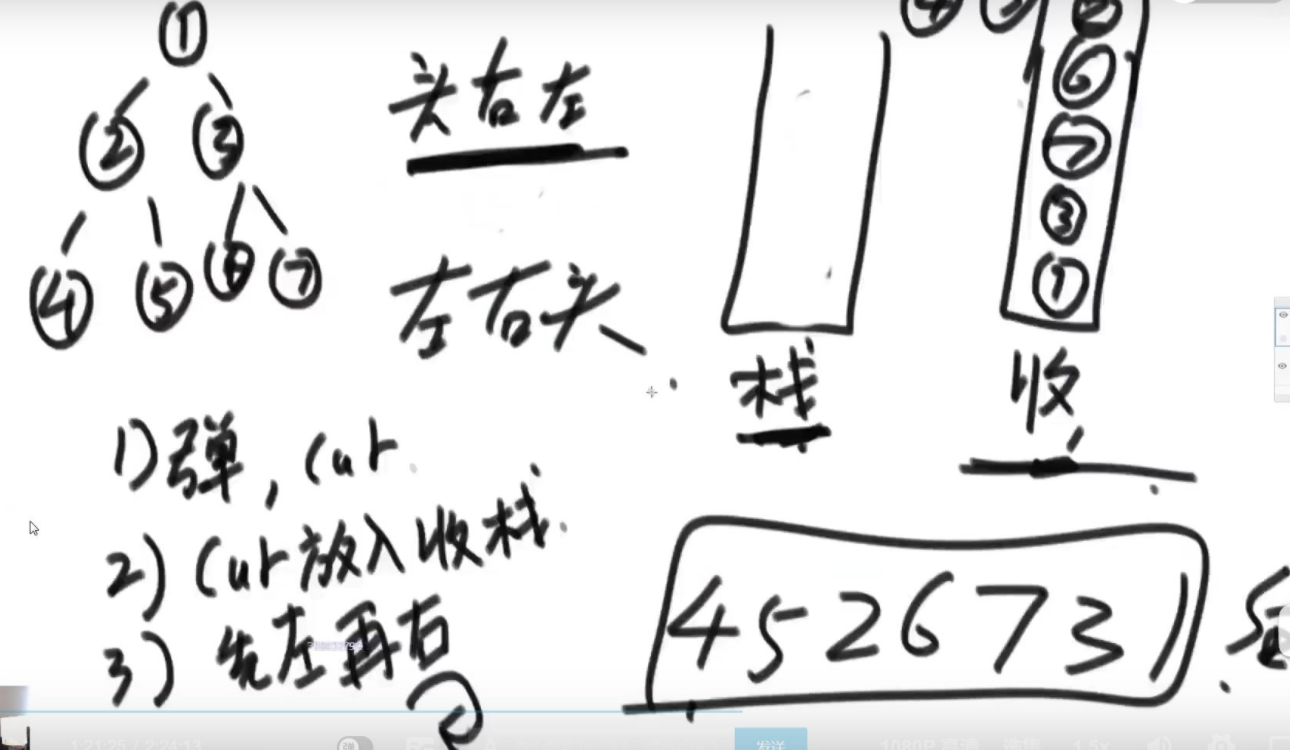
压栈的时候先压入左,后右,得到头左右的顺序,入栈出栈得到左右头的后续遍历
中序遍历
思想
- 整颗树左边进栈
- 依次弹出的过程中,打印
- 对弹出节点的右节点依次操作
求二叉树的宽度(完成二叉树宽度的优先遍历)
宽度优先遍历
的基础上操作
二叉树的相关问题
- 搜索二叉树判断:左树的节点比根节点小,右树的节点比根节点大
判断:中序遍历是升序,是搜索二叉树
- 完全二叉树判断:
- 满二叉树判断
- 平衡二叉树判断:对任何一个子树,左右树的高度差不超过1
要左树,要右数的递归套路
- 给定两个二叉树节点node1和node2, 找到他们的最低公共祖先节点
- 二叉树的序列化和反序列化:内存里的一棵树变成字符串形式/字符串变成内存里的二叉树
- 如何判断一个二叉树是不是另一个二叉树的子树
9. 图
1. 图的存储方式
- 邻接表
点集作为单位:
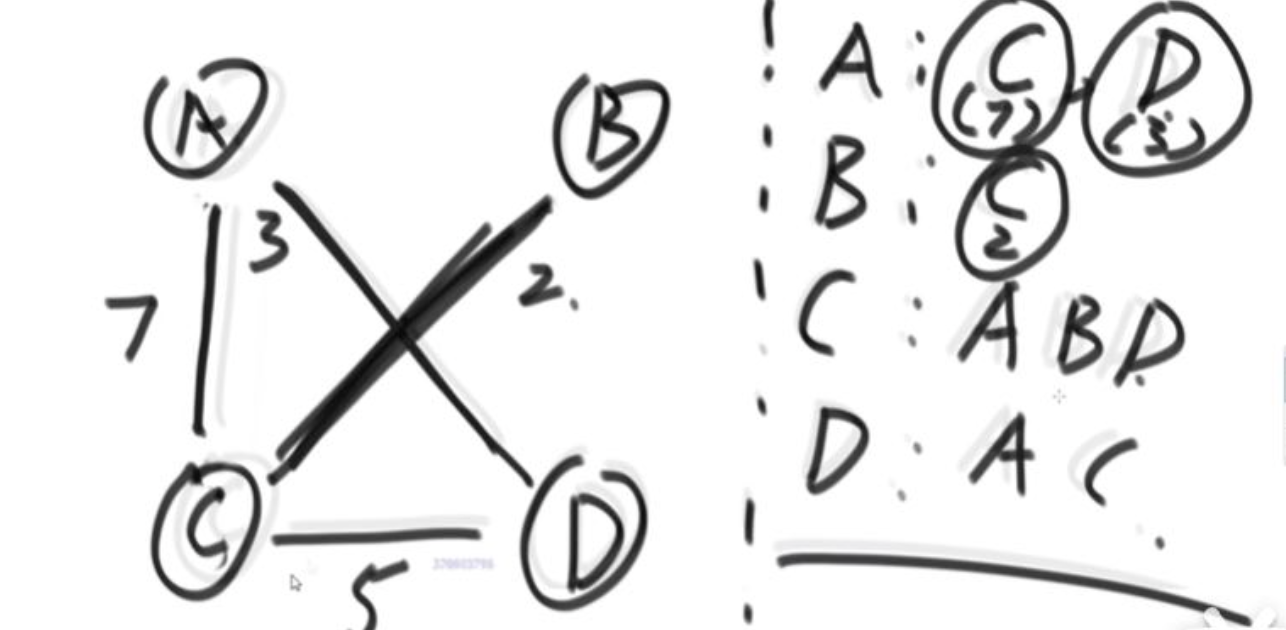
- 邻接矩阵(一定是个正方形)
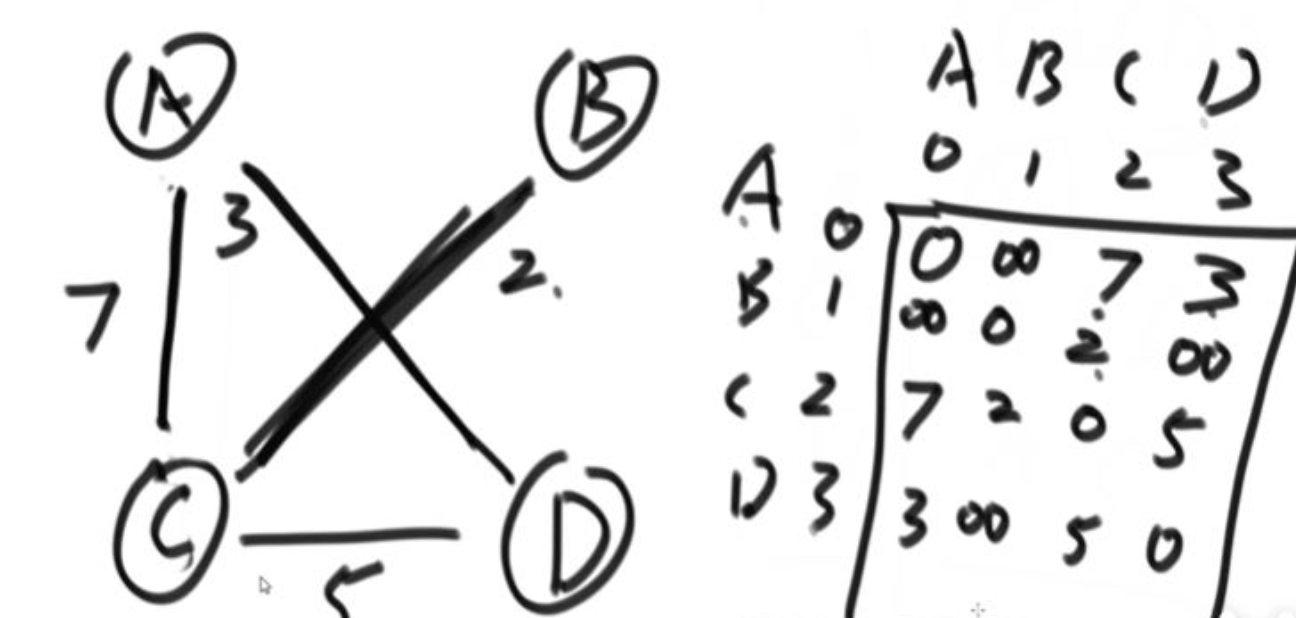
2. graph
class Graph:
def __init__(self):
self.nodes = {}#点集 点序号:Node
self.edges = set()#边集
class Edges:#边
def __init__(self, weight, from_node, to_node):
self.weight = weight
self.from_node = from_node
self.to_node = to_node
class Node:
def __init__(self, value):
self.value = value
self.in_number = 0#入度
self.out_number = 0#出度
self.nexts = []#存连接的Node列表
self.edges = []#存发出的边的列表
3. 写接口
def transfer(matrix):
new_graph = Graph()#新建一个图
for row in matrix:
from_node = row[0]
to_node = row[1]
weight = row[2]
#看from和to节点是不是已经存在与图中
#添加节点到图的nodes里
if from_node not in new_graph.nodes.keys():
new_graph.nodes[from_node] = Node(from_node)
if to_node not in new_graph.nodes.keys():
new_graph.nodes[to_node] = Node(to_node)
#添加边到edges里
new_edge = Edge(weight, from_node, to_node)
new_graph.edges.add(new_edge)
#改变node中的其他值
new_graph.nodes[from_node].out_number += 1
new_graph.nodes[from_node].edges.append(new_edge)
new_graph.nodes[from_node].nexts.append(new_graph.nodes[to_node])
new_graph.nodes[to_node].in_number +=1
#验证
'''
print('node %d in dict, value %d, in_number %d, out_number %d, nextsadd: %d, edgesweight: %d'\
%(from_node, new_graph.nodes[from_node].value, new_graph.nodes[from_node].in_number\
, new_graph.nodes[from_node].out_number, new_graph.nodes[from_node].nexts[-1].value,\
new_graph.nodes[from_node].edges[-1].weight))
'''
return new_graph
matrix = [[1,2,4],[2,3,3],[3,1,7],[3,2,3],[4,1,2]]
G1 = transfer(matrix)
4. 图的宽度优先遍历
非常重要: 在添加node.nexts时判断是否注册过
import queue
def bfs(node):
if node.value == None:
return
q = queue.Queue()#别忘了括号
register = set()#注册表,防止环状
q.put(node)#进队列
register.add(node)#注册
while(not q.empty()):#队列不空时
cur = q.get()
print(cur.value)#替换别的操作
for anode in cur.nexts:#每次进nexts时,添加的nexts都在队列最后面,所以这一层走完才可以走下一层,即宽度优先
if anode not in register:#把没有注册的nodes里面的node进队列,并注册
q.put(anode)
register.add(anode)
matrix = [['A','B',0],['A','C',0],['A','E',0],['B','C',0],['C','E',0],['B','D',0]\
,['B','A',0],['C','A',0],['E','A',0],['C','B',0],['E','C',0],['D','B',0]]
G2 = transfer(matrix)
bfs(G2.nodes['A'])
5. 图的广度优先遍历
Important: 1. 每一层只入栈一个元素,需要break;2. 元素的处理位置在第一次入栈的时候,因为会出入栈好几次。
def dfs(node):
if node.value == None:
return
stack = []
register = set()
stack.append(node)
register.add(node)
print(node.value)#important
while(stack):
cur = stack.pop()
#print(cur.value)
for anode in cur.nexts:
if anode not in register:
stack.append(cur)
stack.append(anode)
register.add(anode)
print(anode.value)#important
break#most important step,在这一层中只看一个node,然后cur也进栈
#记住处理元素的位置,node出栈次数超过一次,所以在第一次进栈的时候处理
6.拓扑排序
#拓扑排序(编译器顺序,先编译入度为0的包,去除这个包和所带来的影响,再找入度为0的包编译)
#要求:单向图,且有0入度的节点,没有环
import queue
def sortedtopology(graph):
Inmap = {}#用来存储node:in_number,来判断要进入队列的节点
zero_in_queue = queue.Queue()
for node_key, node in graph.nodes.items():#生成Inmap,同时找出此时入度为0的节点放入队列
Inmap[node] = node.in_number
if node.in_number == 0:
zero_in_queue.put(node)
result = [] #要给出的列表
while(not zero_in_queue.empty()):#队列不空时,取一个放入返回列表
cur = zero_in_queue.get()
result.append(cur)
for anode in cur.nexts:#抹除当前节点对剩余序列的影响
Inmap[anode] -= 1
if Inmap[anode] == 0:
zero_in_queue.put(anode)
return result
matrix2 = [['d','b',0], ['e', 'b',0],['c','b',0],['e','a',0], ['c','a',0],['b','a',0]]
G2 = transfer(matrix2)
result = sortedtopology(G2)
for node in result:
print(node.value)
7. 最小生成树算法
1. 并查集
class Mysets:
def __init__(self, nodes):
self.mysets = {}# 字典 node:set
for node in nodes.keys():
self.mysets[nodes[node]] = {nodes[node]}#node类:node类的集合
#提供两个函数,一个判断是否连接,一个用来结合起来
def is_same_set(self, from_node, to_node):
from_set = self.mysets[from_node]
to_set = self.mysets[to_node]
return from_set == to_set#判断是不是相同
def union(self, from_node, to_node):
from_set = self.mysets[from_node]
to_set = self.mysets[to_node]
for node in to_set:#把to_set里的节点添加到fromset里去,让to_node的值和from_set相同
from_set.add(node)
#self.mysets[to_node] = from_set
self.mysets[node] = from_set ##most important :把to_set中的node的to_set都改为from_set
'''
测试数据
'''
matrix3 = [['a','b',3],['a','c',100],['a','d',7],['c','a',100],['d','a',7],['b','a',3],\
['c','b',5],['b','c',5],['c','d',100],['d','c',100],['b','d',2],['d','b',2]]
G3 = transfer(matrix3)
mysets = Mysets(G3.nodes)
'''
测试用例
'''
for i in myset.mysets:
for j in myset.mysets[i]:
print(j.value)
myset.union(G3.nodes['a'],G3.nodes['b'])
for node_set in myset.mysets:
print('---------')
for node in myset.mysets[node_set]:
print(node.value)
print('---------')
print(myset.is_same_loop(G3.nodes['a'], G3.nodes['c']))
2. K算法(边思想)
思想:
从最小边开始判断,添加并查看是不是有环
- 对每个节点初始化一个set集合,只有自己在里面
- 对所有的边从小到大排序,从最小的边开始遍历
- 利用并查集判断from节点和to节点的set是否相同
如果不同,把边添加到results中,
from节点的set中添加toset中的所有数据
toset中的所有节点赋值为from节点所指向的set
def k_algorithm(graph):
results = []
mysets = Mysets(graph.nodes)
#判断初始化是否成功
for node, node_set in mysets.mysets.items():
print('node:%s,set:'%(node.value), end = '')
for i in node_set:
print(' %s '%(i.value), end = ' ')
print('')
list_edges = list(graph.edges)
list_edges.sort(key = lambda x:x.weight)
for edge in list_edges:
print('-----------new loop------------------')
print('判断边edge: from %s, to %s, weight %d'%(edge.from_node, edge.to_node, edge.weight))
from_node = graph.nodes[edge.from_node]
to_node = graph.nodes[edge.to_node]
if not mysets.is_same_set(from_node, to_node):
results.append(edge)
mysets.union(from_node, to_node)
#判断loop之后的是否成功
for node, node_set in mysets.mysets.items():
print('node:%s,set:'%(node.value), end = '')
for i in node_set:
print(' %s '%(i.value), end = ' ')
print('')
#判断result是否正确
print('此时的results为:')
for edge in results:
print('edge: from %s, to %s, weight %d'%(edge.from_node, \
edge.to_node, edge.weight), end = ' ')
print('')
return results
#测试数据
lujing = k_algorithm(G3)
for i in lujing:
print('from %s, to %s, weight %d'%(i.from_node, i.to_node, i.weight))
3. P算法(点思想)
1.随机选择一个点开始,注册,在’边‘的优先队列中添加所有的边进去,
2.当优先队列不为空时,取出当前最小边,判断tonode没有注册,注册,边放入results,把tonode的所有边放入队列
import queue
def p_algorithm(graph):
node_register = set()
edge_priorityqueue = queue.PriorityQueue()
results = set()
for node_name in graph.nodes.keys():#解决森林问题,即有些图不是连通图。
node = graph.nodes[node_name]
node_register.add(node)
for edge in node.edges:
edge_priorityqueue.put((edge.weight, id(edge),edge))#当第一项相同时,第二项不相同,most important
#否则报错edge和edge没有实现比较方法
while(not edge_priorityqueue.empty()):
edge = edge_priorityqueue.get()[2]
#print(edge.weight)
to_node_name = edge.to_node
if graph.nodes[to_node_name] not in node_register:
node_register.add(graph.nodes[to_node_name])
results.add(edge)
for smalledge in graph.nodes[to_node_name].edges:
edge_priorityqueue.put((smalledge.weight,id(smalledge), smalledge))
break#没有森林时使用
return results
results = p_algorithm(G3)
for i in results:
print(i.weight)
8. Dijkstra算法
规定一个出发点,算出出发点到每一个节点的最短路径
适用范围:没有权值为负数的边