标签：随想录 window 第五十七 dp new 动态规划 opens 回文

动态规划最强总结篇！

如今动态规划已经讲解了42道经典题目，共50篇文章，是时候做一篇总结了。

关于动态规划，在专题第一篇关于动态规划，你该了解这些！ (opens new window)就说了动规五部曲，而且强调了五部对解动规题目至关重要！

这是Carl做过一百多道动规题目总结出来的经验结晶啊，如果大家跟着「代码随想哦」刷过动规专题，一定会对这动规五部曲的作用感受极其深刻。

动规五部曲分别为：

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

动规专题刚开始的时候，讲的题目比较简单，不少录友和我反应：这么简单的题目讲的复杂了，不用那么多步骤分析，想出递推公式直接就AC这道题目了。

Carl的观点一直都是简单题是用来巩固方法论的。简单题目是可以靠感觉，但后面稍稍难一点的题目，估计感觉就不好使了。

在动规专题讲解中，也充分体现出，这动规五部曲的重要性。

还有不少录友对动规的理解是：递推公式是才是最难最重要的，只要想出递归公式，其他都好办。

其实这么想的同学基本对动规理解的不到位的。

动规五部曲里，哪一部没想清楚，这道题目基本就做不出来，即使做出来了也没有想清楚，而是朦朦胧胧的就把题目过了。

如果想不清楚dp数组的具体含义，递归公式从何谈起，甚至初始化的时候就写错了。
例如动态规划：不同路径还不够，要有障碍！ (opens new window)在这道题目中，初始化才是重头戏
如果看过背包系列，特别是完全背包，那么两层for循环先后顺序绝对可以搞懵很多人，反而递归公式是简单的。
至于推导dp数组的重要性，动规专题里几乎每篇Carl都反复强调，当程序结果不对的时候，一定要自己推导公式，看看和程序打印的日志是否一样。

好啦，我们再一起回顾一下，动态规划专题中我们都讲了哪些内容。

#动态规划基础

#背包问题系列

背包问题大纲

#打家劫舍系列

#股票系列

股票问题总结

#子序列系列

#动规结束语

关于动规，还有树形DP（打家劫舍系列里有一道），数位DP，区间DP ，概率型DP，博弈型DP，状态压缩dp等等等，这些我就不去做讲解了，面试中出现的概率非常低。

能把本篇中列举的题目都研究通透的话，你的动规水平就已经非常高了。对付面试已经足够！

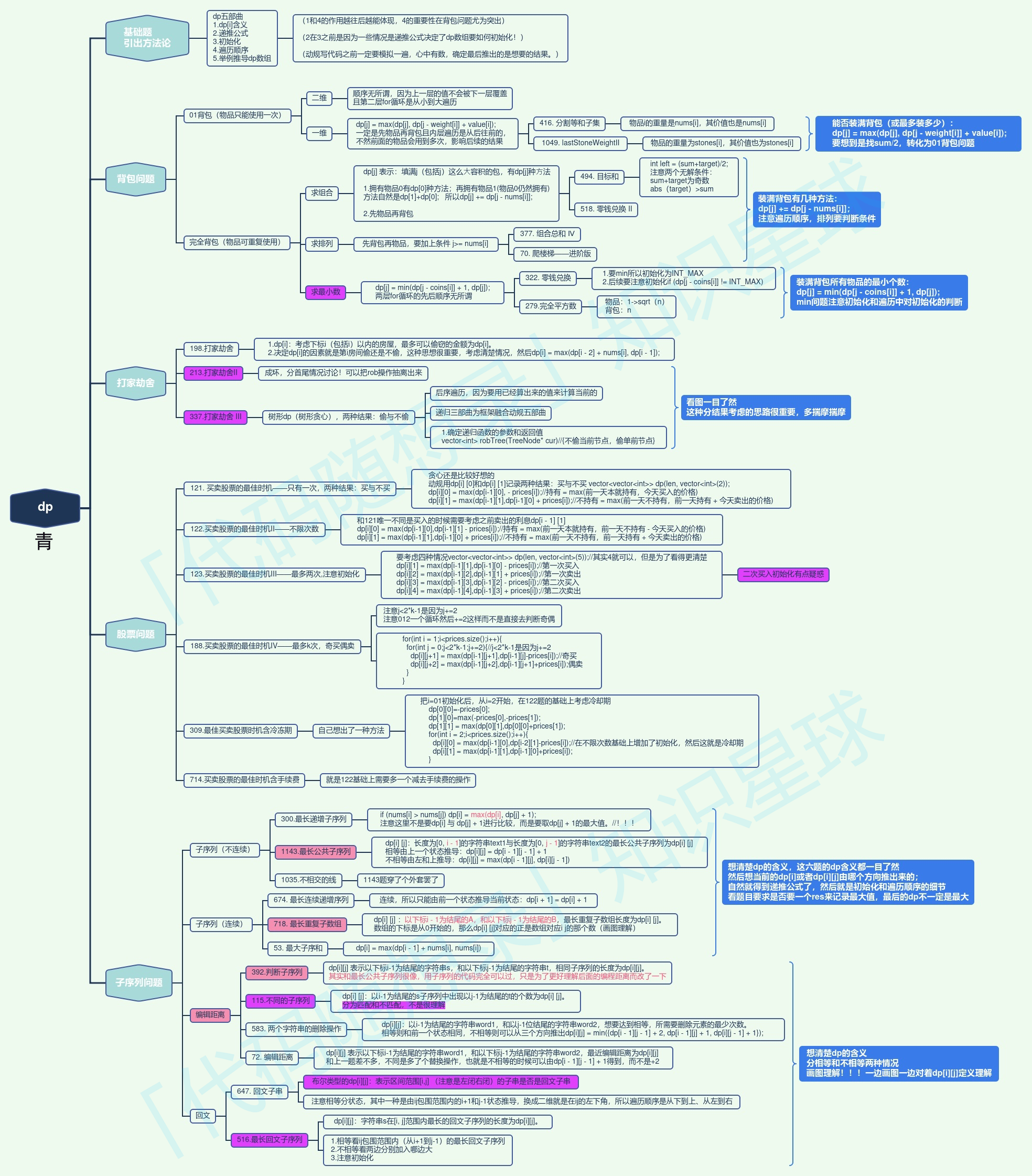
这个图是代码随想录知识星球 (opens new window)成员：青 (opens new window)，所画，总结的非常好，分享给大家。

这应该是全网对动规最深刻的讲解系列了。

其实大家去网上搜一搜也可以发现，能把动态规划讲清楚的资料挺少的，因为动规确实很难！要给别人讲清楚更难！

《剑指offer》上动规的题目很少，经典的算法书籍《算法4》没有讲动规，而《算法导论》讲的动规基本属于劝退级别的。

讲清楚一道题容易，讲清楚两道题也容易，但把整个动态规划的各个分支讲清楚，每道题目讲通透，并用一套方法论把整个动规贯彻始终就非常难了。

所以Carl花费的这么大精力，把自己对动规算法理解一五一十的全部分享给了录友们，帮助大家少走弯路，加油！

647. 回文子串

已解答中等

相关企业

提示

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。

回文字符串 是正着读和倒过来读一样的字符串。

子字符串 是字符串中的由连续字符组成的一个序列。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：

输入：s = "abc"
输出：3
解释：三个回文子串: "a", "b", "c"

示例 2：

输入：s = "aaa"
输出：6
解释：6个回文子串: "a", "a", "a", "aa", "aa", "aaa"

提示：

1 <= s.length <= 1000
s 由小写英文字母组成

package main

func countSubstrings(s string) int { //dp[i][j] 第i为到第j位是否回文子串 //递推公式 dp[i][i] if s[i] == s[j] else dp[i-1][i-1] s[i] != s[j] 0 j-i == 0 为1 //初始化全为0 //从下到上，从左到右 //输出所有有值的，即为结果 dp := make([][]bool, len(s)) for i := 0; i < len(dp); i++ { dp[i] = make([]bool, len(s)) } var res int for i := len(s) - 1; i >= 0; i-- { for j := i; j < len(s); j++ { if i == j { res++ dp[i][j] = true continue } if s[i] != s[j] { continue } if i+1 == j || dp[i+1][j-1] { res++ dp[i][j] = true } } } return res }

516. 最长回文子序列

已解答中等

相关企业

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

示例 1：

输入：s = "bbbab"
输出：4
解释：一个可能的最长回文子序列为 "bbbb" 。

示例 2：

输入：s = "cbbd"
输出：2
解释：一个可能的最长回文子序列为 "bb" 。

提示：

1 <= s.length <= 1000
s 仅由小写英文字母组成

package main

func longestPalindromeSubseq(s string) int { //dp[i][j] i到j子串最小变动次数 //递推公式，dp[i][j] if i == j :0 if i+1 = j s[i]==s[j] 0 else 1 s[i] == s[j] = dp[i][j] = dp[i+1][j-1] else min(dp[i+1][j] , dp[i][j-1])+1 //初始化全为0 //下到上，左到右， // len(num) - dp[0][len(s)] 为答案 dp := make([][]int, len(s)) fori := 0; i < len(dp); i++ { dp[i] = make([]int, len(s)) } fori := len(s) - 1; i >= 0; i-- { forj := i + 1; j < len(s); j++ { if i == j { continue } if i+1 == j { if s[i] != s[j] { dp[i][j] = 1 } } else { if s[i] == s[j] { dp[i][j] = dp[i+1][j-1] } else { dp[i][j] = min(dp[i+1][j], dp[i][j-1])+1 } } } } returnlen(s) - dp[0][len(s)-1] }

func min(a, b int) int { if a > b { return b } return a }

标签：随想录,window,第五十七,dp,new,动态,规划,opens,回文
From： https://www.cnblogs.com/suxinmian/p/18094380

代码随想录算法训练营第五十七/天 | 516. 最长回文子序列，647. 回文子串