KMP 字符串搜索算法

KMP 字符串搜索算法是 Knuth、Morris、Pratt 三位在类似的时间段内一起发明的一种字符串搜索算法，该算法的主要原理是利用待查找子串中的某些信息，在匹配失败时能够减少回退的步数

算法原理

假设现在有一个待搜索的字符串 ABABAC，如何利用现有的字符串实现在字符不匹配时尽可能向后调整搜索的开始位置。

目前主要存在两种处理方式：DFA 和部分匹配表

DFA^[1]

假设通过原有的搜索字符串已经构建了一个 DFA，他能够帮助我们在不匹配的情况下如何移动匹配的开始位置指针。比如，将 ABABAC 构造对应的 DFA，如下图所示：

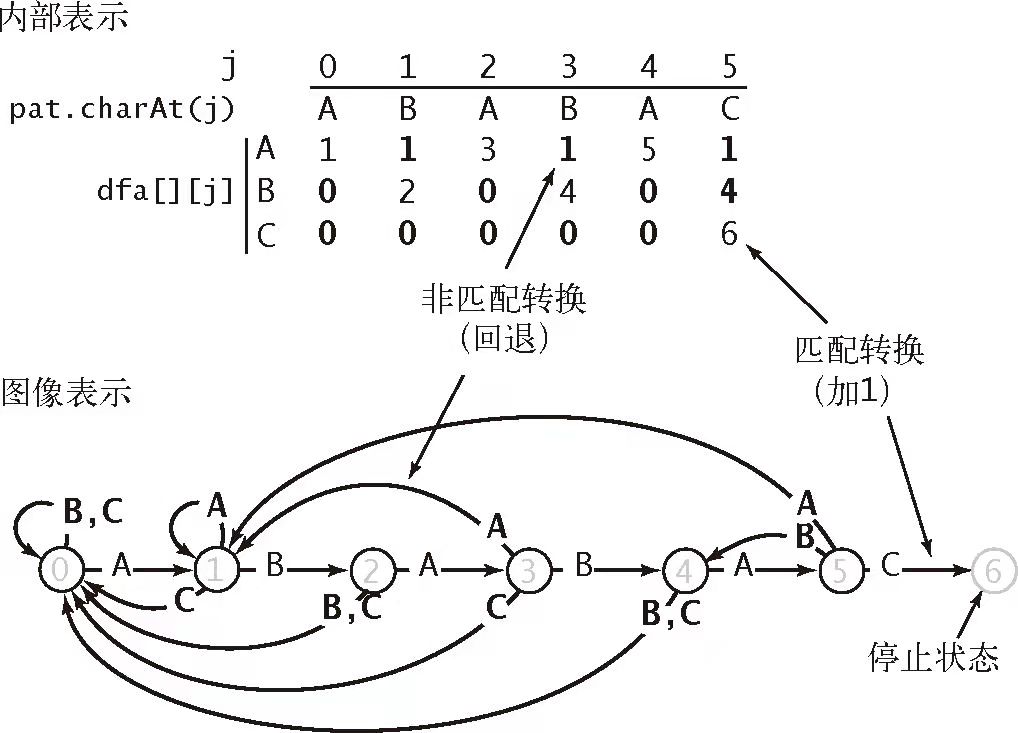
很直观的形式，当匹配过程中遇到某个不匹配的字符时，可以通过这个不匹配的字符重新定位待搜索字符串的开始位置。比如，如果查找的原字符串内容为 BCBAABACAABABAC，那么可能搜索情况如下图所示：

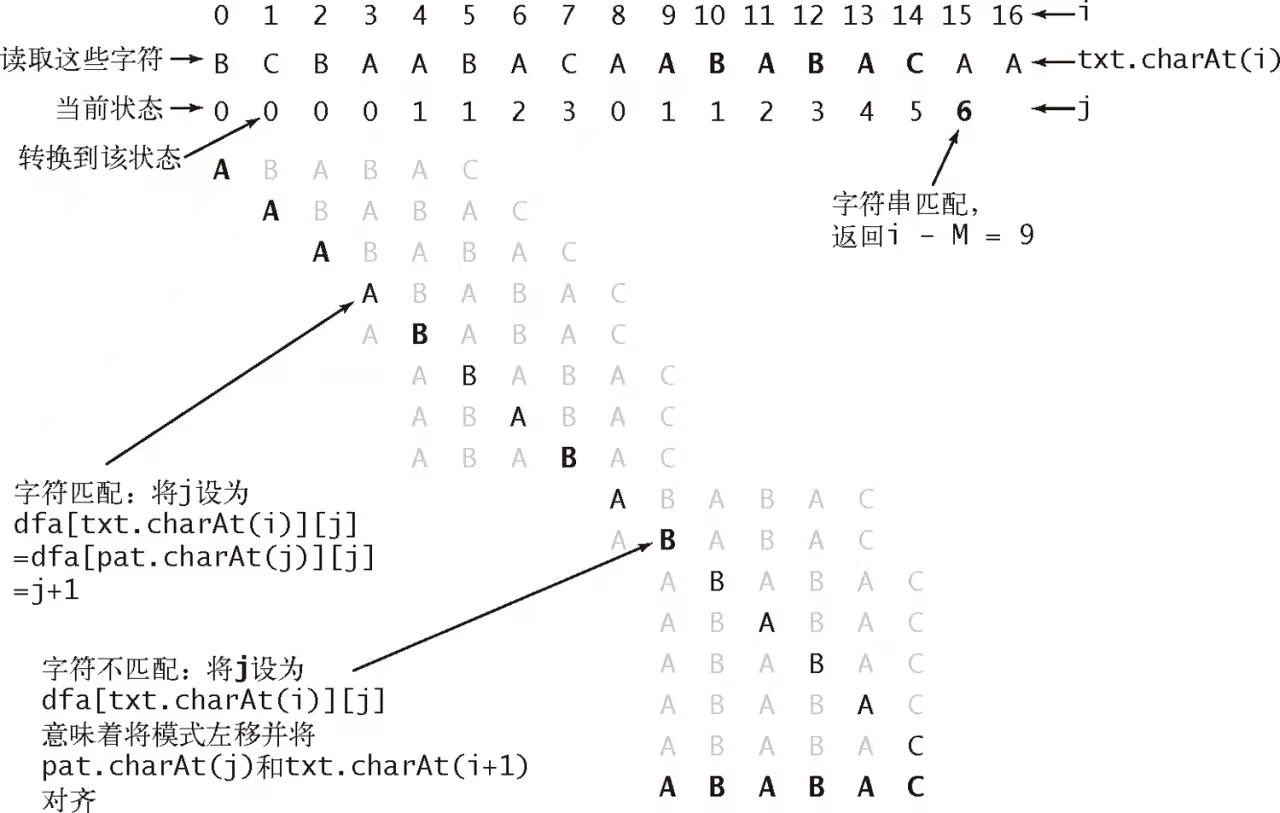
如果存在这样的 DFA，那么在搜索时对应的代码实现如下所示：

public int search(String txt) {
    // 模拟 DFA 处理文本时进行的操作
    int i, j, N = txt.length(), M = pat.length();
    for (int i = 0, j = 0; i < N && j < M; ++i) {
        j = dfa[txt.charAt(i)][j];
    }
    
    if (j == M) return i - M;
    return N;
}

DFA 的使用比较简单，但是如果需要从头开始研究如何构造对应的 DFA，这具有很大的难度。因此，这里仅仅给出构造 DFA 的代码：

public void initDFA() {
    dfa[pat.charAt(0)][0] = 1;
    for (int x = 0, j = 0; j < M; ++j) {
        for (int c = 0; c < R; ++c) {
            dfa[c][j] = dfa[c][x];
        }
        dfa[pat.charAt(j)][j] = j + 1;
        x = dfa[pat.charAt(j)][x];
    }
}

具体构造过程如下图所示：

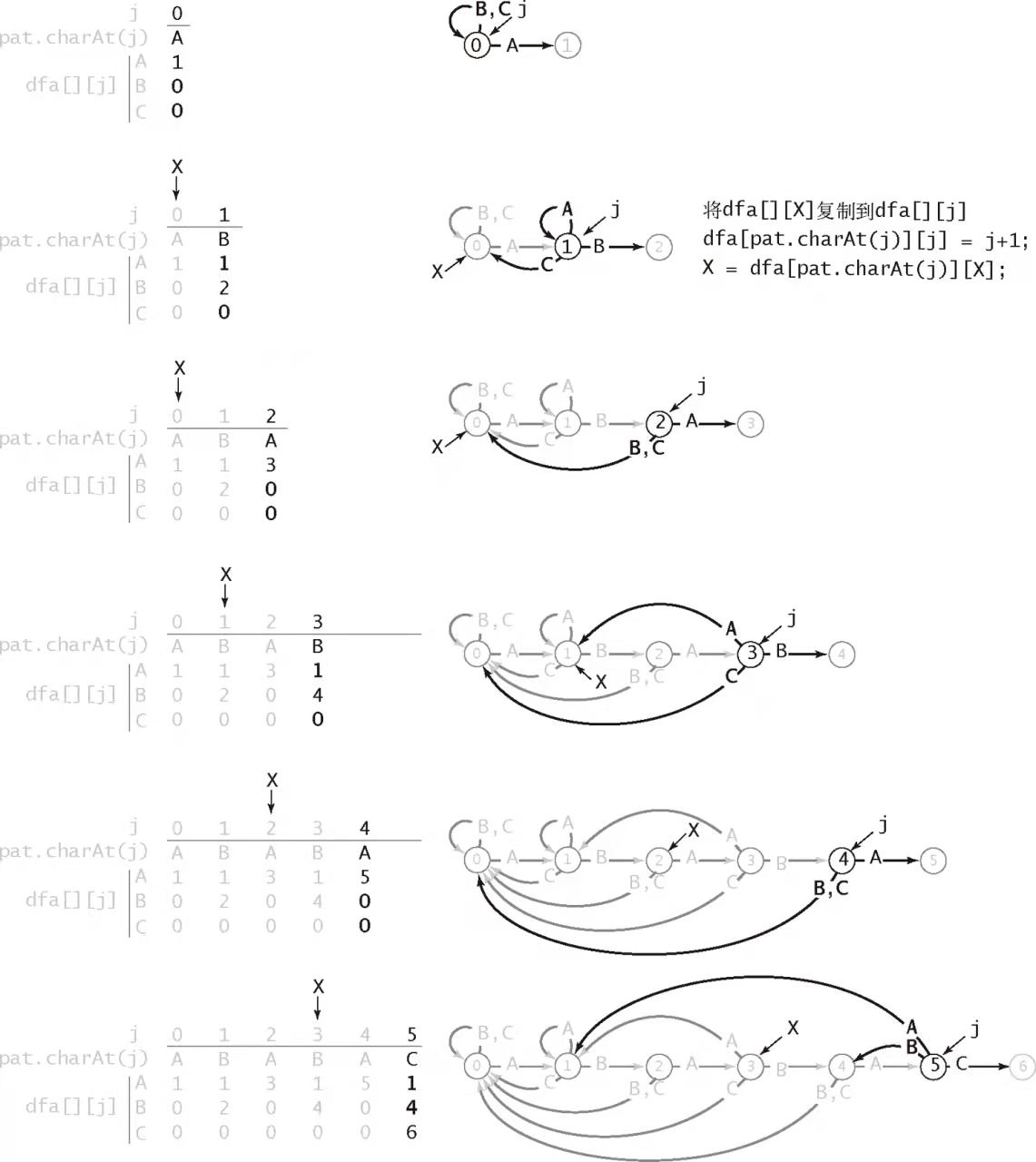
部分匹配表^[2]

首先，了解两个概念：前缀和后缀。“前缀” 是指除了字符串的最后一个字符外，子串的全部头部组合；“后缀” 是指除了首字符外，子字符串的所有尾部组合。

部分匹配表的元素是当前位置的 “前缀” 和 “后缀” 最长共有的元素的长度，比如，对于字符串 ABCDABD 来讲，它的 “部分匹配表” 的产生过程如下：

1. “A” 的前缀和后缀都为空集，公共元素数量为 \(0\)
2. “AB” 的前缀为 “A”，后缀为 “B”，公共元素数量为 \(0\)
3. “ABC” 的前缀为 \([A, AB]\)，后缀为 \([BC, C]\)，公共元素数量为 \(0\)
4. “ABCD” 的前缀为 \([A, AB, ABC]\)，后缀为 \([BCD, CD, D]\)，公共元素的数量为 \(0\)
5. “ABCDA” 的前缀为 \([A, AB, ABC, ABCD]\)，后缀为 \([BCDA, BCD, CD, A]\)，公共元素为 \([A]\)，长度为 \(1\)
6. “ABCDAB” 的前缀为 \([A, AB, ABC, ABCD, ABCDA]\)，后缀为 \([BCDAB, CDBAB, DAB, AB, B]\)，共有的公共元素为 \([AB]\)，长度为 \(2\)
7. “ABCDABD‘ 的前缀为 \([A, AB, ABC, ABCD, ABCDA, ABCDAB]\)，后缀为 \([BCDABD, CDABD, DABD, ABD, BD, D]\) 公有长度为 \(0\)

因此，最后产生的部分匹配表如下图所示：

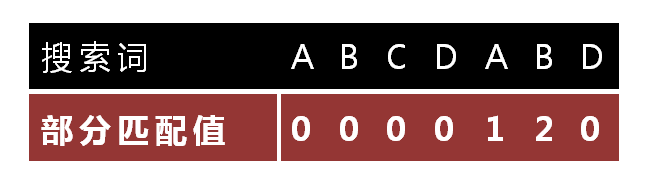
当搜索时，通过

移动相应的匹配搜索开始位置

实现

• DFA 的实现如下：

  public class KMP {
      private final String pat;
      private final int[][] dfa;
      private final int R;
      private final int m;
  
      public KMP(String pat) {
          this.pat = pat;
          R = 256;
          m = pat.length();
          dfa = new int[R][m];
          
          dfa[pat.charAt(0)][0] = 1;
          for (int x = 0, j = 1; j < m; ++j) {
              // 复制不匹配的情况下的状态
              for (int c = 0; c < R; ++c) {
                  dfa[c][j] = dfa[c][x];
              }
  
              dfa[pat.charAt(j)][j] = j + 1; // 设置匹配成功时的状态
              x = dfa[pat.charAt(j)][x]; // 更新重启状态
          }
      }
  
      public int search(String txt) {
          int n = txt.length();
          int i, j;
          for (i = 0, j = 0; i < n && j < m; ++i)
              j = dfa[txt.charAt(i)][j];
  
          if (j == m) return i - m;
          return n;
      }
  }
  

• “部分匹配表“ 的实现如下：

  import java.util.Arrays;
  import java.util.HashSet;
  import java.util.Set;
  
  public class KmpPartTable {
      private final String pat;
      private final int[] next;
  
      public KmpPartTable(String pat) {
          this.pat = pat;
          int m = pat.length();
  
          next = new int[m];
          next[0] = 0;
          for (int i = 1; i < m; ++i) {
              Set<String> set = new HashSet<>();
              // 计算前缀集合
              for (int j = 0; j < i; ++j) {
                  set.add(pat.substring(0, j));
              }
  
              // 计算后缀集合
              for (int j = 1; j <= i; ++j) {
                  String str = pat.substring(j, i + 1);
                  if (set.contains(str) && str.length() > next[i])
                      next[i] = str.length();
              }
          }
  
          System.out.println(Arrays.toString(next));
      }
  
      public int search(String txt) {
          int m = pat.length(), n = txt.length();
          int i, j;
          for (i = 0, j = 0; i < n && j < m;) {
              int k = i, cnt = 0;
              while (k < n && j < m) {
                  if (txt.charAt(k) == pat.charAt(j)) {
                      k++;
                      j++;
                      continue;
                  }
  
                  cnt = (j + 1) - next[j];
                  break;
              }
  
              if (j >= m) break;
              i += cnt;
          }
  
          if (j == m) return i - m;
          return n;
      }
  }
  

参考：

^[1] 《算法（第四版）》

^[2] https://www.ruanyifeng.com/blog/2013/05/Knuth–Morris–Pratt_algorithm.html