1. KMP 算法
KMP 算法,是判断一个字符串是否在一个字符串中出现过,能够快速匹配字符串在文本串中的有无,位置,次数,我们在匹配字符串中可以找到失配点,就可以不用从 \(1\) 重新查找,从某个特定点进行查找,大大减小了时间复杂度。
考虑一组样例:
字符串:abcdf
文本串:abcdabcdef
我们来将他匹配,首先前 \(4\) 个字母都会匹配上,发现到了第 \(5\) 个,就匹配不上了。那么我们就将字符串移动到失配的点。
字符串: abcdf
文本串:abcdeabcdef
因此我们可以不用一位一位的找,就可以根据相同的字母来进行匹配。
一共有两步:先是处理 KMP 数组,接着是字符串匹配。
在处理 KMP 数组中,我们可以自己匹配自己,对于每个 j 并且
j 是拥有可继承性的。
fup(i, 2, l2) {
while (j && s2[i] != s2[j + 1]) {
j = kmp[j];
}
if (s2[j + 1] == s2[i]) {
j++;
}
kmp[i] = j;
}
在进行字符串匹配,j 可以看做表示当前已经匹配完的模式串的最后一位的位置,如果失配,那么就不断向回跳,直到可以继续匹配,如果匹配成功,那么对应的模式串位置 \(++\)。
fup(i, 1, l1) {
while (j > 0 && s2[j + 1] != s1[i]) {
j = kmp[j];
}
if (s2[j + 1] == s1[i]) {
j++;
}
if (j == l2) {
j = kmp[j];
}
}
例题:模板。
2.TIRE 树
TIRE 树,能够判断一个字符串的前缀,在多个字符串是否出现过,在查询时,通过判断每个字符的前缀,从而减少时间复杂度。在建树中,通过公共前缀来减少空间。
我们来举个例子:怎么存 abc,abb,bca,bc。
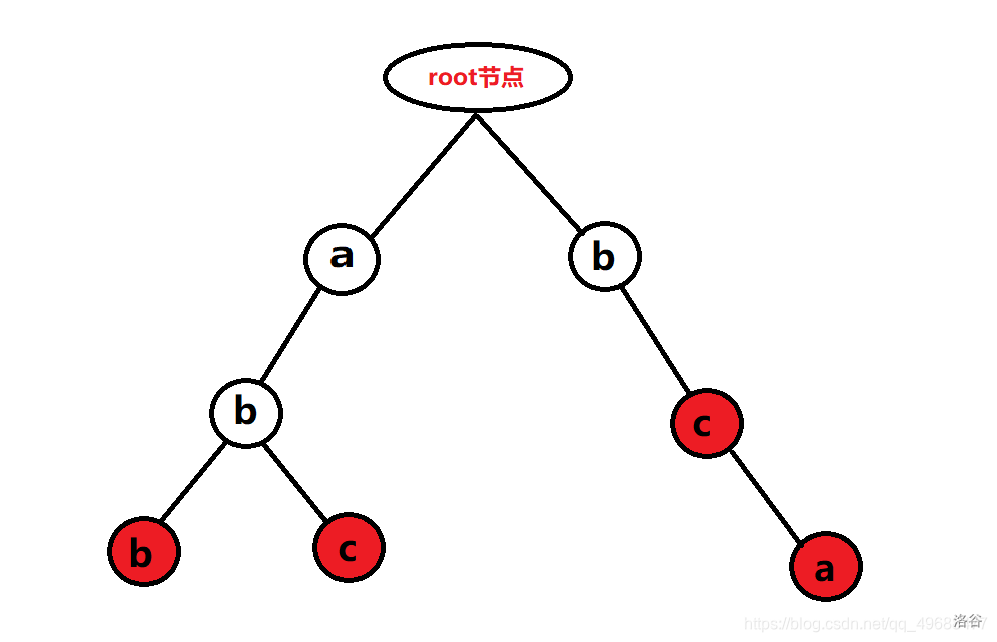
通过这样存,就能够将这些所有的字符串存起来。
在用字典树中,也需要两步,先将字符串插入,在进行查询。
在进行插入时,通过一个二维数组,id 表示每个节点的编号,每个 \(tire[i][x]\) 表示一条边,\(1-n\) 表示每个节点的编号,如果 \(tire[i][x]==0\) 表示 i 这个点没有边,而 \(cnt[i]!=0\) 表示这个点不是叶节点,它还能继续往下拓展字符,p 代表节点编号,通过 \(tire[p][x]\) 判断当前节点是否存在,在插入时,如果 p 节点没有边,那么就 \(++id\) 将这个边存上,最后将 p 更新成新节点的编号。
void insert(string s) {
int p = 0;
fup(i, 0, s.size() - 1) {
int x = s[i]-'a';
if (trie[p][x] == 0) trie[p][x] = ++id;
p = trie[p][x];
cnt[p]++;
}
}
接着进行查询,其他都差不多,就在 \(tire[p][x]==0\) 时表示这个点就确实没有出现过了,因此我们返回 \(0\) 查找失败,最后如果要求每个字符串前缀出现的次数,那么就返回 \(cnt[p]\),表示每个字符串前缀的次数。
int find(string s) {
int p = 0;
fup(i, 0, s.size() - 1) {
int x = fun(s[i]);
if (trie[p][x] == 0) return 0;
p = trie[p][x];
}
return cnt[p];
}
例题:模板。
标签:匹配,TIRE,++,s2,算法,KMP,字符串,节点 From: https://www.cnblogs.com/gongyuchen/p/18026197