备考考点整理
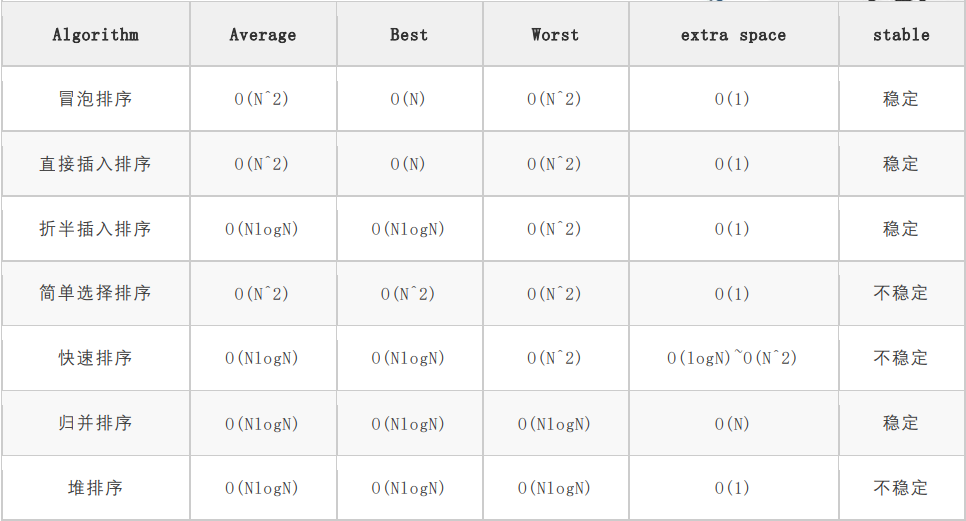
内部排序表格
树的主要考点
二叉树的常考
紧紧抓住
\(n_0 = n_2+1\)
\(n=n_0+n_1+n_2...n_m\)
\(n=n_1+2*n_2+3*n_3...m*n_m\) +1
哈夫曼树没有度为1的结点,也就是\(n_1=0\)



完全二叉树常考

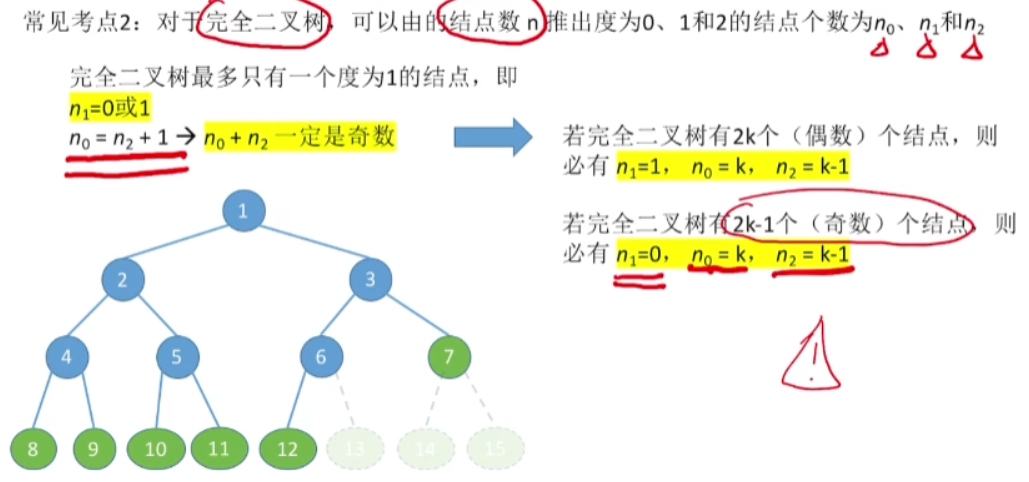
总结

最大岛屿问题(dfs模板)

#include <iostream>
#include <algorithm>
using namespace std;
const int maxn =1000;
int grid[maxn][maxn]; //网格
int num=0;
int m,n; //m行n列
void dfs(int x,int y){
grid[x][y] = 0; //改写成0
int dx[4]={-1,0,1, 0};
int dy[4]={ 0,1,0,-1}; //四个方向
for(int i=0;i<4;i++){
int a = x + dx[i];
int b =y + dy[i];
if(a>=0 && b >=0 && a<m && b<n && grid[a][b]==1){
num++;
dfs(a,b);
}
}
}
int maxArea(){
int ans = 0;
for(int i=0;i<m;i++)
for(int j=0;j<n;j++){
if(grid[i][j]==1){
num=1;
dfs(i,j);
}
ans = max(ans,num); //最大岛屿面积
}
return ans;
}
int main(){
cin >>m>>n;
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
cin>>grid[i][j];
cout<<"最大岛屿面积"<<maxArea();
return 0;
}
DFS的模板:
此处dfs模板可以背
//答案版
#include<iostream>
#include<algorithm>
using namespace std;
int amax = 0;
int n;
int a[1000][1000];
void dfs(int i,int j,int &sum)
{
if(i==-1||j==n||i==n||j==-1||a[i][j]==0) return;//走出边界或者路走不通
else
{
a[i][j] = 0; //将走过的路标记为走不通
sum++;
}
dfs(i-1,j,sum);//搜索四个方向的路
dfs(i,j-1,sum);
dfs(i+1,j,sum);
dfs(i,j+1,sum);
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
cin>>a[i][j];
}
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
if(a[i][j]>0)
{
int sum=0;//记录最大路
dfs(i,j,sum);
amax=max(sum,amax);
}
}
cout<<amax;
return 0;
}
计算二叉树双分支结点(递归)

双端队列实现
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=100;
struct deque{
int arr[maxn];
int head;
int tail;
int size=0;
};
deque que;
que.head=que.tail=0;
que.size=0;
void head_in(deque &que,int x){
if(que.size==n)
return;
que.arr[que.head] = x;
if(que.head == 0)
que.head=n-1;
else
que.head--;
}
void head_out(deque &que,int &x){
if(que.size==0)
return;
que.arr[que.head] = x;
if(que.head == n-1)
que.head=0;
else
que.head++;
}
void tail_in(deque &que,int x){
if(que.size==n)
return;
if(que.head == n-1)
que.head=0;
else
que.head++;
que.arr[que.head] = x;
}
void tail_out(deque &que,int x){
if(que.size==0)
return;
if(que.head == 0)
que.head=n-1;
else
que.head--;
que.arr[que.head] = x;
}
递归分治
递归概念
直接或间接地调⽤⾃⾝的算法称为递归算法。⽤函数⾃⾝给出定义的函数称为递归函数
边界条件与递归⽅程是递归函数的两个要素
递归优点缺点
递归⼩结
优点:结构清晰,可读性强,⽽且容易⽤数学归纳法来证明算法的正确性,因此它为设计算法、调试程序带来很⼤⽅便。
缺点:递归算法的运⾏效率较低,⽆论是耗费的计算时间还是占⽤的存储空间都⽐⾮递归算法要多。 解决⽅法:在递归算法中消除递归调⽤,使其转化为⾮递归算法。
递归生成全排列
回溯法
void Perm(int list[],int i,int n)
{
if(i==n)
{
for(int i=1;i<=n;i++)
cout<<list[i];
cout<<endl;
}
for(int t=i;t<=n;t++)
{
swap(list[t],list[i]);
Perm(list,i+1,n);
swap(list[t],list[i]);
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>list[i];
Perm(list,1,n);
return 0;
}
1.树到叶子结点sum路径匹配
给定一个二叉树T和一个值 sum , 判断是否有从根节点到叶子节点的节点值之和等于 sum的路径。 找出一条路径使得路径上各个结点值的和等于sum:
int check(TreeNode *T,int sum)
{
if(T == NULL && sum == 0)
return 1;
if(T == NULL && sum !=0)
return 0;
return check(T->lchild,sum - T->data) || check(T->rchild,sum-T->data);
}
2,判断树是否轴对称
如果一个树的左子树与右子树镜像对称,那么这个树是对称的。因此,该问题可以转化为:两个树在什么
情况下互为镜像?
如果同时满足下面的条件,两个树互为镜像:它们的两个根结点具有相同的值,每个树的右子树都与另一
个树的左子树镜像对称。
我们可以实现这样一个递归函数,通过「同步移动」两个指针的方法来遍历这棵树,p 指针和 q 指针一
开始都指向这棵树的根,随后 p 右移时,q 左移,p 左移时,q 右移。每次检查当前 p 和 q 节点的值是否相等,如果相等再判断左右子树是否对称。
int check(TreeNode *p, TreeNode *q)//初始化q,p都指向根节点
{
if (!p && !q) return true;//都为空
if (!p || !q) return false;//结构不对称
return p->data == q->data && check(p->left, q->right) && check(p->right, q->left);
}
int isSymmetric(TreeNode* root)
{
return check(root, root);//初始时候p,q都指向根节点
}
3.整数划分
对于正整数n的划分,最⼤加数不⼤于m的个数记作q(n,m)
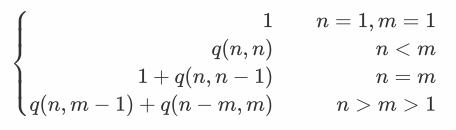
int fun(int n,int m)//表示求解
{
if(m==1) //最⼤加数不超过1,只有⼀种划分
return 1;
if(n<m) //最⼤加数不能⼤于 要划分的数字n
return fun(n,n);
if(n==m)
return 1+fun(n,n-1); //取n本身作为⼀种划分⽅案 + 最⼤加数⼩于n的所有⽅案
return fun(n,m-1)+fun(n-m,m); //⽅案分为 含有最⼤加数 和不含最⼤加数两种
}
4.二分法求幂函数
这里的二分是指减少乘法的次数,把重复的运算省去。我要求 x 的 n 次方,那么先求 x 的 n/2 次方,然
后两个相乘起来。如此递归下去。
核心思想:x^n
1.递归结束条件
n==0;return 1;
2.递归转移方程
if n%2==1;x* x^(n/2) * x^(n/2)
n%2==0 x^(n/2) * x^(n/2)
double fun(double x, int n)
{
if (n == 0)//递归结束条件
return 1;
double half;
if (n %2== 1)//递归转移方程
{
half = fun(x, n / 2);//x的n/2次方
return x*half*half;
}
else
{
half = fun(x, n / 2);
return half * half;
}
}
5.最大字段和(分治法)
int n;
int arr[Maxn];
struct Status
{
//lSum 表示该 Status 从左端连续最大子段和,rSum 表示从右段连续最大子段和,mSum表示整段的最大子段和,iSum 表示整段求和
int lSum, rSum, mSum, iSum;
};
struct Status pushUp(struct Status l, struct Status r)
{
int iSum = l.iSum + r.iSum;
int lSum = max(l.lSum, l.iSum + r.lSum);
int rSum = max(r.rSum, r.iSum + l.rSum);
int mSum = max(max(l.mSum, r.mSum), l.rSum + r.lSum);
return (struct Status){lSum, rSum, mSum, iSum};//回溯的结果
}
struct Status get(int* a, int l, int r)
{
//递归的边界条件
if (l == r)
{
return (struct Status){a[l], a[l], a[l], a[l]};
}
int m = (l + r) >> 1;
struct Status lSub = get(a, l, m);
struct Status rSub = get(a, m + 1, r);
return pushUp(lSub, rSub);//向上回溯
}
int maxSubArray(int* nums, int numsSize)
{
return get(nums, 0, numsSize - 1).mSum;
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
cin>>arr[i];
cout<<maxSubArray(arr,n)<<endl;
return 0;
}
动态规划
- dp数组含义
- 递推公式
- dp数组初始化
- dp数组遍历顺序,先物品?先背包?
- 打印dp数组
1.硬币凑金额问题
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
int dp[maxn];//dp[i]表示用coins来凑i元需要的最少金额
int n;
int coins[maxn]={INT_MAX};
int fun(int amount)
{
dp[0]=0;
for(int i=1;i<=amount;i++)//背包
for(int j=0;j<n;j++)//物品
if(i>=coins[j] && dp[i-coins[j]]!=INT_MAX)
{
dp[i]=min(dp[i-coins[j]]+1,dp[i]);
}
if(dp[amount]==INT_MAX)
return -1;
else
return dp[amount];
}
2. 一维dp,爬楼梯最小耗费
dp[i] 到达i位置的最小耗费
dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
3.二维dp,不同路径
//明确是走多少步还是多少种!!
dp[i][j]是走到ij格子有多少种不同的路径
dp[i][j]=dp[i-1][j]+dp[i][j-1]
//初始化
dp[0][j]=1
dp[i][0]=1
4.二维dp,不同路径2
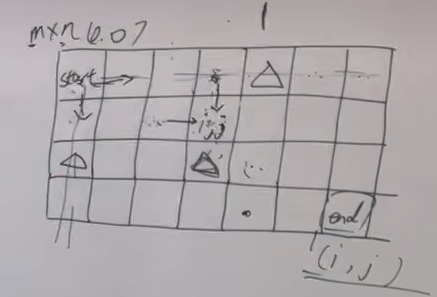
//图中有障碍
if(obs[i][j]==0)//没有障碍
dp[i][j]=dp[i-1][j]+dp[i][j-1]
//初始化
for(int i=0;i<m && obs[i][0]==0 ;i++)
dp[i][0]=1; //遇到障碍后面全是0
for(int j=0;j<n && obs[0][j]==0 ;j++)
dp[0][j]=1; //后面全是0
5. 一维,整数拆分
dp[i] //对i进行拆分,得到最大乘积为dp[i]
//分拆成两个数和拆成两个数以上
for(int i=3;i<=n;i++) //n是数字
for(int j=1;j<i;j++) //j是拆
dp[i]=max(j*(i-j),j*dp[i-j],dp[i]);
6.不同形状的二叉搜索树
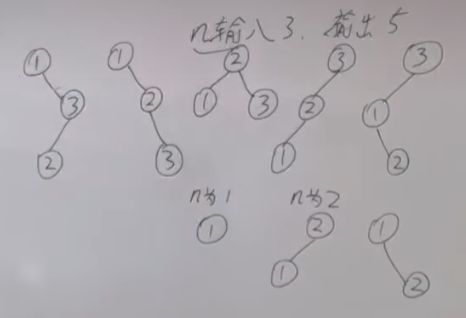
n=3 头1+头2+头3
头1 = 左子树0结点 * 右子树2结点
头2 = 左子树1结点 * 右子树1结点
头3 = 左子树2结点 * 右子树0结点
dp[3]=dp[0]*dp[2]+dp[1]*dp[1]+dp[2]*dp[0]
dp[i]:有dp[i]种不同的二叉搜索树
for(i=1;i<=n;i++)
for(j=1;j<=i;j++)
dp[i] += dp[j-1]*dp[i-j];
7. 0-1背包
dp[i][j]
[0,i]物品任取放容量为j的背包
dp[i][j]
不放物品i:dp[i-1][j]
放物品i:dp[i-1][j-w[i]] + v[i]
初始化
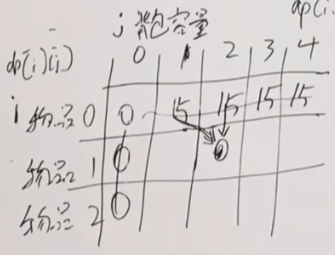
最大字段和(动规)dp[i]表示,以i为结尾的数组的最大子段和是多少

class Solution {
public:
int maxSubArray(vector<int>& nums) {
int res = nums[0];
for(int i = 1; i < nums.size(); i++) {
if (nums[i - 1] > 0) nums[i] += nums[i - 1];
if (nums[i] > res) res = nums[i];
}
return res;
}
};
int n;
int arr[Maxn];
int solve(int arr[])
{
int dp[Maxn]={0};//dp[i]表示,以i为结尾的数组的最⼤⼦段和是多少
dp[1]=arr[1];
int ans=dp[1];
for(int i=2;i<=n;i++)
{
dp[i]=max(arr[i],arr[i]+dp[i-1]);
ans=max(ans,dp[i]);
}
cout<<"ans="<<ans<<endl;
}
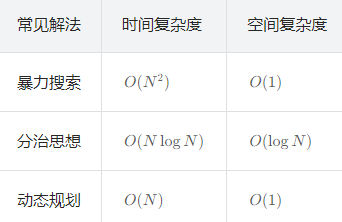
8.分割等和子集(母体!!凡是联想到分成两个子集)
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
0-1背包能否装满问题
target = sum /2
dp[j] 容量为j,最大价值为dp[j]
判断条件dp[target]==target
dp[j]=max(dp[j],dp[j-w[i]]+v[i])
--> dp[j]=max(dp[j-nums[i]]+nums[i]) //重量等于价值
for(i=0;i<=nums.size();i++) //先物品
for(j=target;j>=nums[i];j--) //后背包(因为做了状态压缩,顺序不能调换)
 正序倒叙的区别
正序倒叙的区别
9.最后一块石头的重量2
和上一题一样
最后凑不成dp[target]==target也没关系
dp[j] 容量为j,最大重量为dp[j]
dp[j]=max(dp[j],dp[j-w[i]]+v[i])
//先物品再背包
剩下sum-dp[j]-dp[j]就是剩下的最小的石头
int lastStoneWeightII(vector<int>& stones) {
int dp[3001]={0};
int sum=0;
for(int i=0;i<stones.size();i++)
sum+=stones[i];
for(int i=0;i<stones.size();i++)
{
for(int j=sum/2;j>=stones[i];j--)
dp[j] = max(dp[j],dp[j-stones[i]]+stones[i]);
}
return sum-2*dp[sum/2];
}
10.股票买卖问题
int maxProfit(vector<int>& prices) {
int dp[100000][2]={0};
//0是持有,1是未持有
dp[0][0]=-prices[0];
dp[0][1]=0;
for(int i=1;i<prices.size();i++)
{
dp[i][0]=max(dp[i-1][0],0-prices[i]);
dp[i][1]=max(dp[i-1][1],dp[i-1][0]+prices[i]);
}
return dp[prices.size()-1][1];
}
11.目标和(0-1背包装满有多少种方法母体)
//left是正,right是负
left+right=sum
left-right=target
target=sum/2
所以left=(target+sum)/2 //如果left无法被2整除,直接返回0就行,凑不出来
dp[j] 装满容量j的背包有dp[j]种方法
//要凑5 =凑1的种类+凑4的种类 + 凑2的种类+凑3的种类
dp[5]=dp[1]+dp[2]+dp[3]+dp[4]
dp[j]+=dp[j-nums[i]] !!!!!(装满有多少种的母体)
int findTargetSumWays(vector<int>& nums, int target) {
int sum = 0;
for (int i = 0; i < nums.size(); i++) sum += nums[i];
if (abs(target) > sum) return 0; // 此时没有方案
if ((target + sum) % 2 == 1) return 0; // 此时没有方案
int bagSize = (target + sum) / 2;
vector<int> dp(bagSize + 1, 0);
dp[0] = 1;
for (int i = 0; i < nums.size(); i++) {
for (int j = bagSize; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[bagSize];
}
12. 一和零
dp[i][j] i个0,j个1 最大背了dp[i][j]个物品
每一个数有x个0、y个1
max(dp[i-x][j-y]+1,dp[i][j])
dp[0][0]=0 非0下标:0
13.完全背包
//0-1背包 一维dp从后往前遍历
for(int i;i<weight.size();i++) //物品
for(int j=bagweight;j>=weight[i];j--) //背包
dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);
//完全背包
for(int i;i<weight.size();i++) //物品
for(int j=weight[i];j<=bagweight;i++) //背包
dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);
14.零钱兑换问题2
dp[j] 装满容量j的背包有dp[j]种方法
dp+=dp[j-coins[i]];
dp[0]=1;
先物品,再背包 得到组合数
for(i=0;i<coins.size;i++)//物品
for(j=coins[i];j<=amount;j++) //背包
先背包,在物品,得到排列数
for(j=coins[i];j<=amount;j++) //背包
for(i=0;i<coins.zie;i++)//物品
//先物品,再背包 得到组合数
//先背包,在物品,得到排列数
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
vector<int> dp(1000,0);
vector<int> coins;
int n,amount;
void carryfirst(int amount)
{
dp[0]=1;
for(int i=0;i<coins.size();i++)//先物品
for(int j=coins[i];j<=amount;j++)//再背包
dp[j]+=dp[j-coins[i]];
}
void bagfirst(int amount)
{
dp[0]=1;
for(int j=0;j<=amount;j++)//先背包
for(int i=0;i<coins.size();i++)//再物品
if(j>=coins[i])
dp[j]+=dp[j-coins[i]];
}
int main()
{
cin>>n;
for(int i=0;i<n;i++){
int temp;
cin>>temp;
coins.push_back(temp);
}
cin>>amount;
bagfirst(amount);
for(int i=0;i<=amount;i++)
cout<<dp[i]<<" ";
return 0;
}
三维dp
带有分段、逐个
for(int r=2;r<=n;r++){//区间长度
for(int i=0;i<=n-r;i++){//区间起始位置
int j=i+r-1;//区间结束位置
for(int k=i;k<=j-1;k++){//区间划分位置
1.字母乘法表问题
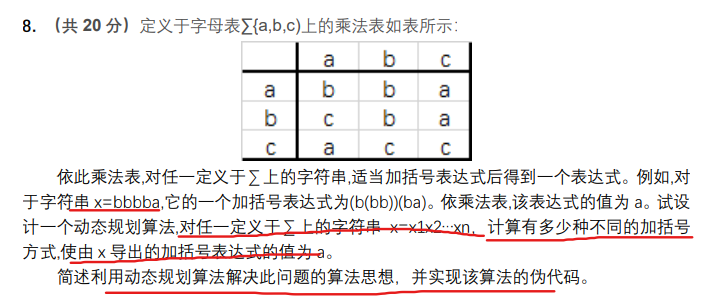
//设字符串的第 i 到 第 j 位乘积为 a 的加括号法有 dp[i][j][a] 种,
//字符串的第 i 到 第 j 位乘积为 b 的加括号法有 dp[i][j][b] 种,
//字符串的第 i 到 第 j 位乘积为 c 的加括号法有 dp[i][j][c] 种。
char table[3][3]={
{'b','b','a'},
{'c','b','a'},
{'a','c','c'},
};
int dp[64][64][3]={0};
int main() {
string s;
cin>>s;
int n=s.length();
for(int i=0;i<n;i++){//1 个字母,对应 dp 值为 1
dp[i][i][s[i]-'a']=1;
}
for(int r=2;r<=n;r++){//区间长度
for(int i=0;i<=n-r;i++){//区间起始位置
int j=i+r-1;//区间结束位置
for(int k=i;k<=j-1;k++){//区间划分位置
dp[i][j][0]+=dp[i][k][0]*dp[k+1][j][2]+dp[i][k][1]*dp[k+1][j][2]+dp[i][k][2]*dp[k+1][j][0];
dp[i][j][1]+=dp[i][k][0]*dp[k+1][j][0]+dp[i][k][0]*dp[k+1][j][1]+dp[i][k][1]*dp[k+1][j][1];
dp[i][j][2]+=dp[i][k][1]*dp[k+1][j][0]+dp[i][k][2]*dp[k+1][j][1]+dp[i][k][2]*dp[k+1][j][2];
}
}
}
cout<<dp[0][n-1][0]<<endl;
return 0;
}
贪心
简单
1.最优装载问题
核心思想:如何装集装箱才能在称重量一定的轮船上装的集装箱最多。按照从轻到重对集装箱进行排序,越轻的
就越先装使得剩余的载重量最大那么就可以装更多的集装箱。
int n;//n 个集装箱
int c;//轮船载重
struct container
{
int id;//编号
int w;//重量
int vis;//是否被装入轮船 1被装入轮船 0
};
container arr[Maxn];
bool cmp(container a,container b)//按照重量排序,在sort里调用一下就可以
{
return a.w<b.w;
}
void solve()
{
int sum=0;//轮船中已经装入的重量
for(int i=1;i<=n;i++)
{
if(sum+arr[i].w<=c)//当前集装箱可以装入
{
sum+=arr[i].w;
arr[i].vis=1;
}
else
break;
}
}
int main()
{
cin>>n>>c;//输入集装箱的个数和最大载重量
for(int i=1;i<=n;i++)
{
cin>>arr[i].w;
arr[i].id=i;
arr[i].vis=0;
}
sort(arr+1,arr+n+1,cmp);//对集装箱按照从轻到重排序
solve();
for(int i=1;i<=n;i++)
if(arr[i].vis==1)
cout<<arr[i].id<<'\t';
cout<<endl;
return 0;
}
分支限界法
(1)队列式(FIFO)分支限界法
按照队列先进先出(FIFO)原则选取下一个节点为扩展节点。
(2)优先队列式分支限界法
按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点。
特征是使用到队列
布线问题(典例)
布线问题。 在 m 行 n 列的网格中, 能否从一个起始位置, 布线到结束位置。 方向只能(上下左右),其中有些位置已 经布线则不能重复布线
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
int grid[100][100];
int m,n;
int dir[4][2]={0,1,1,0,0,-1,-1,0};
int sx,sy,fx,fy;
typedef struct Node
{
int x;
int y;
int step;
}Node;
void func()
{
queue<Node> que;
Node now;
now.x = sx;
now.y = sy;
now.step = 0;
que.push(now);
while(!que.empty())
{
now = que.front();
que.pop();
if(now.x==fx && now.y==fy){
cout << "yes";
return ;
}
Node next;
for(int i=0;i<4;i++)
{
next.x=now.x+dir[i][0];
next.y=now.y+dir[i][1];
next.step=now.step+1;
if(next.x>0 && next.x<=m && next.y>0&&next.y<=n&&grid[next.x][next.y]==0)
{
que.push(next);
grid[next.x][next.y]=1;
}
}
}
}
int main()
{
cin>>m>>n;
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
cin>>grid[i][j];
cin>>sx>>sy>>fx>>fy;
fun();
return 0;
}
回溯法
标准c++回溯法全排列
void perm(int i,vector<int>& nums,vector<vector<int>> &result)
{
if(i==nums.size())
{
result.push_back(nums);
}
else
{
for(int t=i;t<nums.size();t++)
{
swap(nums[i],nums[t]);
perm(i+1,nums,result);
swap(nums[i],nums[t]);
}
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> vec;
perm(0,nums,vec);
return vec;
}
1.批作业调度问题
核心思想:n个作业需要先在机器1上处理再在机器2上处理,不同的处理顺序所需要的最终时间不同,找出一个最小时间和的调度方案。先对作业定义一个结构体(编号、time1,time2),用回溯法的排列树来做(每进入一层(加入一个作业)需要加上在机器1的处理时间,和机器二的处理时间(如果当前作业想在机器二上处理得先保证它在机器1上处理完成,并且前一个作业在机器2上完成了),当回溯回来得时候需要减去在机器1的时间和机器2的时间)。当整个排列树结束,如果所需要的时间<bestf(存储目前的最优值,用的时间最少的顺序);bestf=当前时间
#include <iostream>
using namespace std;
int n; //作业数
int M[100][100]; //M[i][j]表示第i个作业在机器j上需要处理的时间
int x[100]; //x[i]表示第i个处理的作业为x[i]
int bestx[100]; //x[i]的最优值
int f1; //作业在机器1上完成处理的时间
int f2[100]; //f2[i]表示第i个作业在机器2上完成处理的时间
int f; //用于记录前i个作业在机器2上完成处理的时间和
int bestf=10000; //f的最优值
void Backtrack(int i)
{
if(i>n) //每到达一个叶子结点,一定是产生了一个最优解,因此要更新之前最优解的值
{
if(f<bestf) //更新最优解
{
for(int j=1;j<=n;j++)
bestx[j]=x[j];
bestf=f;
}
}
else
{
for(int j=i;j<=n;j++) //控制展开i-1层结点的各个分支。
{
f1+=M[x[j]][1]; //计算第i层(个)作业在机器1上的完成处理的时间
if(f2[i-1]>f1) //如果第(i-1)个作业在机器2上的完成处理的时间大于第i个作业在机器1上的完成处理的时间,那么第i个作业想进入机器2,就要等第(i-1)个作业在机器2上完成后再说
f2[i]=f2[i-1]+M[x[j]][2];
else //否则,第i个作业可以在机器1上完成处理后直接进入机器2。
f2[i]=f1+M[x[j]][2];
f+=f2[i]; //计算完第i个作业在机器2上的完成处理的时间,就可以计算出前i个作业在机器2上完成处理的时间和了
if(f<bestf) //截止到这,已经得到一个前i个作业在机器2上完成处理的时间和f,如果f比之前记录的前i个作业在机器2上的完成处理的时间和的最优值bestf都要小,就可以生成第i层结点的孩子结点,继续探索下一层
{
Swap(x[i],x[j]);
Backtrack(i+1);
Swap(x[i],x[j]);
}
f-=f2[i];
f1-=M[x[j]][1];
}
}
}
int main()
{
cin>>n;
for(int i=1;i<=2;i++)
{
for(int j=1;j<=n;j++)
cin>>M[j][i];
}
for(int i=1;i<=n;i++)
x[i]=i; //初始化排列顺序
Backtrack(1);
for(int i=1;i<=n;i++)
cout<<bestx[i]<<" ";
cout<<bestf<<endl;
return 0;
}
2.括号对数问题
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。 (括号仅限小括号:”()”)
关键点在于:从左往右来任何一个位置左括号的数量不能小于右括号的数量
#include<iostream>
#include<algorithm>
using namespace std;
int n;
char txt[1000];
bool isok(int b,int i)
{
if(i>b){
for(int t=b;t<i;t++)
if(txt[t]==txt[i])
return false;
}
return true;
}
bool check()//生成的括号是否合法
{
int left=0;
for(int i=1;i<=2*n;i++)
{
if(txt[i]=='(')
left++;
else
left--;
if(left<0)//表示出现的右括号数量大于左括号的数量
return false;
}
return true;
}
void perm(int i)
{
if(i==2*n)
{
if(check())
{
for(int i=1;i<=2*n;i++)
cout<<txt[i];
cout<<endl;
return;
}
}else{
for(int t=i;t<=2*n;t++)
{
if(isok(i,t))
{
swap(txt[i],txt[t]);
perm(i+1);
swap(txt[i],txt[t]);
}
}
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
txt[i]='(';
for(int j=n+1;j<=2*n;j++)
txt[j]=')';
perm(1);
return 0;
}
3.汽车装载问题(两辆汽车)
//第 i 个物品放入 1 车中
skc1[top1++]=i;
BackTrack(i+1,c1+w[i],c2);
//回溯
top1--;
//第 i 个物品放入 2 车中
skc2[top2++]=i;
BackTrack(i+1,c1,c2+w[i]);
//回溯
top2--;
#include <bits/stdc++.h>
using namespace std;
int C1,C2;
int skc1[64],skc2[64],top1=0,top2=0;
int n,w[64];
void BackTrack(int i,int c1,int c2){
//剪枝
if(c1>C1||c2>C2)return;
//如果全部货物都已装好
if(i==n){
cout<<"第一个货车:";
for(int t=0;t<top1;t++){
cout<<w[skc1[t]]<<" ";
}
cout<<endl<<"第二个货车:";
for(int t=0;t<top2;t++){
cout<<w[skc2[t]]<<" ";
}
return;
}
//第 i 个物品放入 1 车中
skc1[top1++]=i;
BackTrack(i+1,c1+w[i],c2);
//回溯
top1--;
//第 i 个物品放入 2 车中
skc2[top2++]=i;
BackTrack(i+1,c1,c2+w[i]);
//回溯
top2--;
}
int main(int argc, char** argv) {
cin>>C1>>C2;
cin>>n;
for(int i=0;i<n;i++){
cin>>w[i];
}
BackTrack(0,0,0);
return 0;
超基础超可能考
顺序表
## 顺序表默认结构体
typedef struct
{
int data[maxsize];
int length;
}Sqlist;
1.顺序表递增有序,插入元素x,任然有序
void insert(Sqlist &L,int x)
{
int i=0;
while(L->data[i]<x && i<L->length) //定位到要插入的位置
{
i++;
}
for(int j=L->length-1;j>=i;j--)
{
L->data[i+1] = L->data[i];
}
L->data[i] = x;
L->length++; //不要忘记
}
2.用顺序表最后一个元素覆盖整个顺序表中最小元素,并返回该最小元素
int fun(Sqlist &L)
{
int min=L->data[0];
int j;
for(int i=0;i<L->length;i++)
{
//遍历寻找最小
if(min<L->data[i])
min=L->data[i];
j=i;
}
L->data[j]=L->data[L->length-1];
L->length--;
return L->data[j];
}
3.顺序表元素逆置
void fun(Sqlist &L)
{
int i=0;
int j=L.length-1;
while(i<j)
{
swap(L.data[i],L.data[j]);
i++;
j--;
}
}
4. 删除顺序表中所有值为x的元素
void func(Sqlist &L,int x) //扫描+前移操作
{
int k=0;
for(int i=0;i<L.length;i++)//遍历
{
if(L.data[i]!=x)
L.data[k]=L.data[i];
k++;
}
//不要忘记
L.length = k;
}
void func(Sqlist &L,int x)
{
int k=0;
for(int i=0;i<L.length;i++)
{
if(L.data[i] == x)
k++;
else
L.data[i-k]=L.data[i];
}
L.length=L.length-k;
}
5.两个递增有序表合成一个递增有序表
//归并
//直接用数组了
void fun(int arr1[],int n1,int arr2[],int n2,int temp[])
{
int i=0,j=0;
int t=0;
while(i<n1 && j<n2)
{
if(arr1[i]<arr2[j])
temp[t++]=arr1[i++];
else
temp[t++]=arr2[j++];
}
while(i<n1)
temp[t++]=arr1[i++];
while(j<n2)
temp[t++]=arr2[j++];
}
6.设计一个时间上尽可能高效的算法,找出数组中未出现的最小正整数
必做题
int find(int arr[],int n)//长度为n
{
int temp[maxn];
for(int k=0;k<n;k++)//初始化为0
temp[k]=0;
for(int i=0;i<n.i++)//遍历arr
{
if(A[i]>0 && A[i]<=n)//序号小
temp[A[i]-1] = 1;
}
for(int i=0;i<n;i++)
if(temp[i]==0)
return i+1;
return n+1;
}
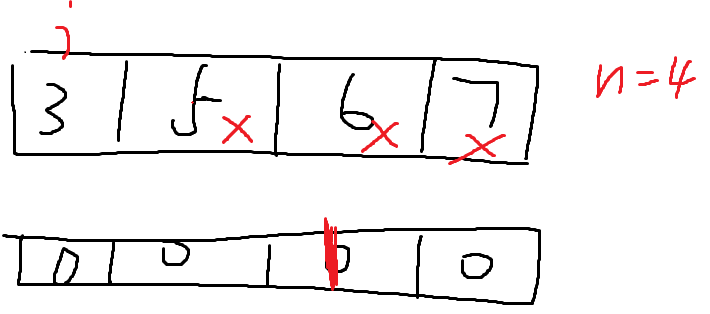
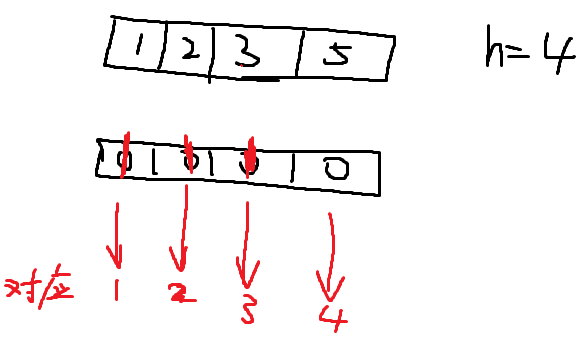
思路是扫描,超出数组大小的不管,额外开拓数组从0到n,出现标记1,没有出现默认0
扫描完成再扫描额外数组,找没出现的值;
链表
//单链表默认结构体
typedef struct LNode
{
int data;
struct LNode *next;
}LNode,*Linklist;
1.删除带头节点单链表中所有值为 x 的结点
void delete(Linklist &L,int x)
{
LinkNode *p=L;
while(p->next != NULL) //不用双指针法
{
if(p->next->data != x)
p=p->next;
else //p->next->data == x
{
LNode *q=p->next;
p->next = q->next;
free(q);
}
}
}
2.删除带头结点单链表的第一个值为x的结点
基础
bool delete(Linklist &L,int x)
{
LNode *p=L; //p扫描
LNode *q; //q执行删除
while(p->next != NULL)
{
if(p->next->data == x)
break;
p=p->next;
}
if(p->next == NULL)//如果p是最后一个,也就是扫描没扫到x
return false;
else
{
q=p->next;// p --- q
p->next = q->next;
free(q);
return ture;
}
}
3.带头结点单链表的逆置
超级重要
void func(Linklist &L)
{
LNOde *p=L->next,*q; //p指第一个数据,q是p的后面一个
L->next=NULL; //L断开 脱离
while(p!=NULL) //重新排序
{
q=p->next;
p->next=L->next;
L->next=p;
p=q;
}
}
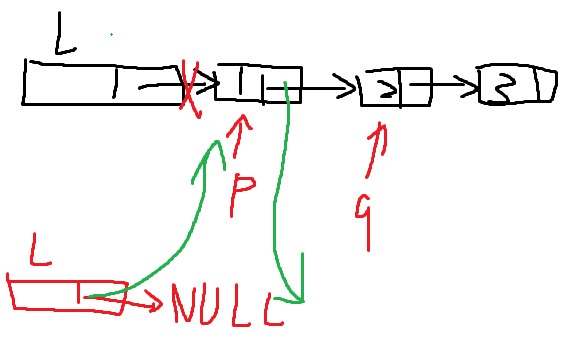
第二种
思路:先把后面的结点逆置了,再连接上头结点
void reverse(Linklist &L) //先逆置每一个next
{
LNode *p=L->next,*r=p->next;
LNode *pre;
p->next = NULL;
while(r != NULL)
{
pre = p;
p=r;
r=r->next;
p->next=pre;
}
L->next=p;
}
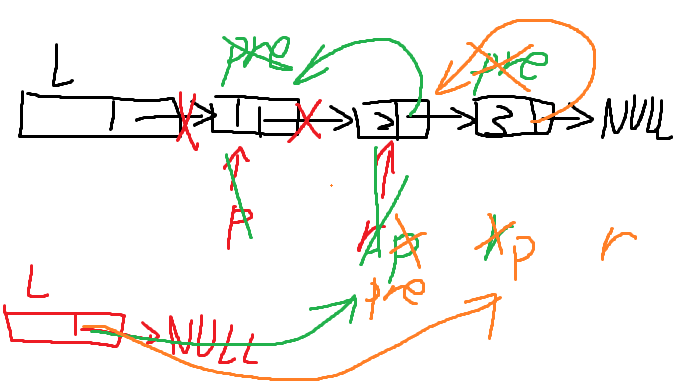
4、在带头结点的单链表 L 中删除最小值点的高效算法(已知最小值唯一)
//快慢指针
void delete_min(Linklist &L)
{
if(L->next ==NULL)
return ;
LNOde *p=L->next;
LNOde *min=L;
while(p->next != NULL) //快指针扫描
{
if(p->next->data < min->next>data) //慢指针维护最小
m=p;
p=p->next;
}
LNOde *u = min->next;//删除操作
min->next = u->next;
free(u);
}
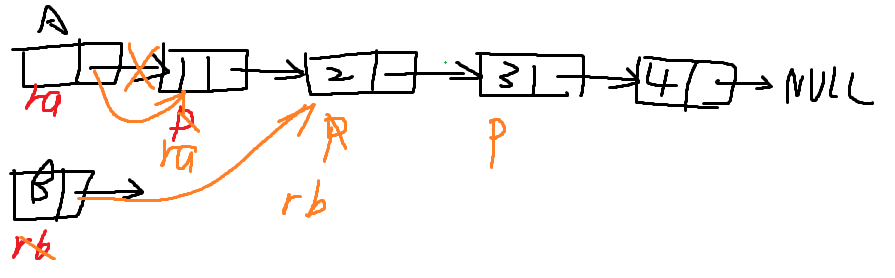
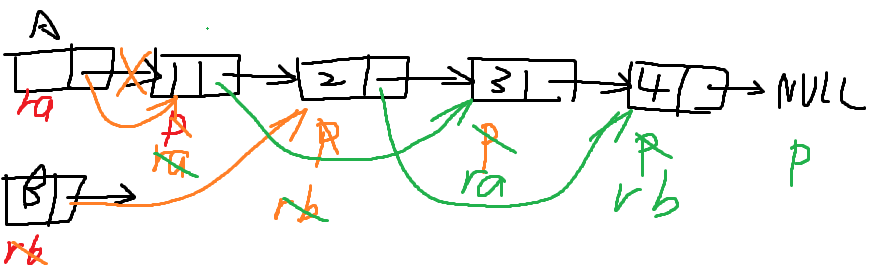
5.将一个带头节点单链表 A 分解成两个带头节点的单链表 A 和 B,使 A 中含奇数位置元素, B 中含偶数位置元素,且相对位置不变
Linklist create(Linklist &A)
{
LNode *B = new LNode;
B->next=NULL;
LNode *ra = A;
LNode *rb = B;
LNode *p= A->next;
A->next=NULL; //断开 分离出数据链
while(p!=NULL)//遍历
{
ra->next=p;
ra=p;
p=p->next;
rb->next=p;
rb=p;
if(p!=NULL)
p=p->next;
}
ra->next=NULL; //记得补充!!
// 两个一组两个一组 rb的末尾肯定是NULL
return B;
}
6、两个递增有序的单链表,设计算法成一个非递减有序的链表。
非递减不是递增
void func(Linklist &L1,Linklist &L2,Linklist &temp)
{
LinkNode *r=temp;
LinkNode *p=L1->next;
LinkNode *q=L2->next;
L1->next=NULL;
L2->next=NULL;//断开L1,L2
while(p!=NULL && q!=NULL)
{
if(p->data <= q->data)
{
temp->next=p;
p=p->next;
temp=temp->next;
}else
{
temp->next=q;
q=q->next;
temp=temp->next;
}
if(p!=NULL)
temp->next=p;
if(q!=NULL)
temp->next=q;
}
}
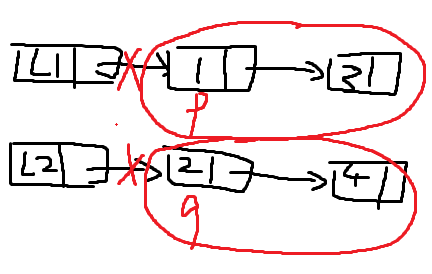
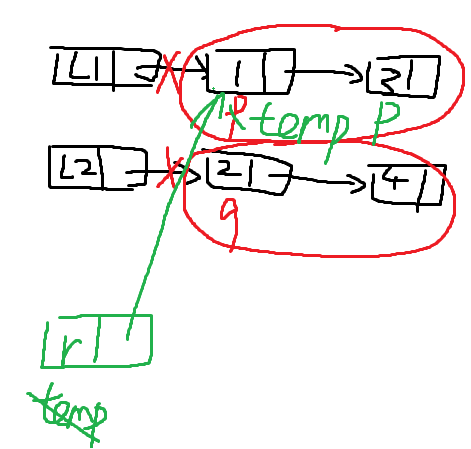
7. A, B两个单链表递增有序,从 A, B 中找出公共元素产生单链表 C,要求不破环 A, B结点
Linklist common(Linklist A,Linklist B)
{
//充分利用A,B递增有序这个条件
LNode *p=A->next;
LNode *q=B->next;
LNode *C = new Lnode;
LNOde *r=C,*s;
while(p!=NUll && q!=null)
{
if(p->data > q->data)
q = q->next;
else if(p->data < q->data)
p = p->next;
else //两个相等
{
s=new LNode;
s->data = p->data;
r->next=s;
r=s;//跟随指针,尾插法!!!
p=p->next;
q=q->next;
}
}
r->next=NULL;
return C;
}
尝试使用两个for/while 来写通用的
void common(Linklist A,Linklist B,Linklist &C)
{
LinkNode *q=A->next;
LinkNOde *p=B->next;
LinkNnode *i=C,*s;
while(q!=NULL)
{
while(p!=NULL)
{
if(q->data == p->data)
{
//不破坏AB
s = new LNOde;
s->data = q->data;
i->next=s;
i=s;
}
p=p->next;
}
q=q->next;
}
}
8、查找单链表中倒数第 k个结点,若成功,则输出该节点的data,并返回 1,否则返回0
int fun(Linklist L,int k)
{
int length=0;
LNode *p = L->next;
while(p!=NULL)
{
length++;
p=p->next;
}
if(length<k)
return 0;
int m=length-k+1;
int i=0;
while(i<m){
L=L->next;
i++
}
//for(int i=0;i<length-k+1;i++)
// L=L->next;
cout<< L->data;
return 1;
}
9、用单链表保存 m 个整数,且|data|≤n,要求设计时间复杂度尽可能高效的算法,对于 data 绝对值相等的点,仅保留第一次出现的点(408 必会)
//时间换空间 一遍遍历就可以
void fun(Linklist &L)
{
LinkNode *p=L;
LinkNode *r;
int arr[n+1]={0};
int k;
while(p->next != NULL)
{
if(p->next->data > 0) //不能直接改,要先检查再改
k=p->next->data;
else
k=- p->next->data;
if(arr[k]==0)//没出现 可以修改
{
arr[k]=1;
p=p->next;
}else//出现过了
{
r=p->next;
p->next=r->next;
free(r);
p=p->next;
}
}
}
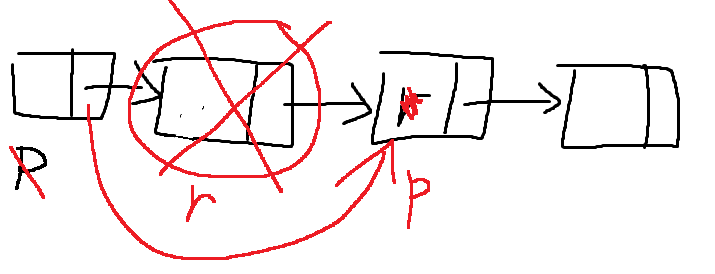
10、判断带头结点的循环双链表是否对称
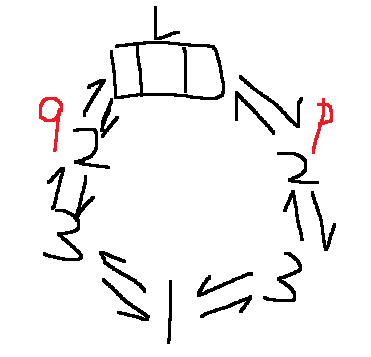
//双链表很方便 可以直接定位到首位
int fun(DoubleList L)
{
DNode *p=L->next;
DNode *q=L->prior;
while(p != q && q->next != p) //结点数是当双数的情况下从首位往中间推
{
if(p->data == q->data)
{
p=p->next;
q=q->prior;
}else{
return 0;
}
}
return 1;
}
11、有两个循环单链表,链表头指针分别为 h1,h2, 试编写函数将 h2 链表接到 h1 之后,要求链接后仍保持循环链表形式
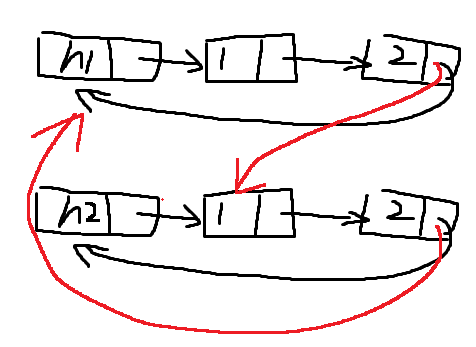
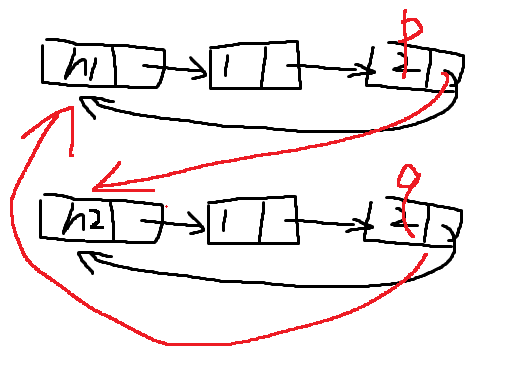
//这种方式里面包含最后的链表里面包含头结点
void link(Linklist &h1,Linklist &h2)
{
LNode *p=h1;
LNode *q=h2;
while(p->next!=h1)
p=p->next;
while(q->next!=h2)
q=q->next;
p->next=h2;
q->next=h1;
}
12、判断单链表是否有环
直接背诵
//思想用快慢指针来实现
int findloop(Linklist *L)
{
LNode *fast=L;
LNode *slow=L;
while(fast && fast->next)
{
slow=slow->next;
fast=fast->next>next;
if(slow == fast)
return 1;
}
return 0;
}
栈
栈的结构体
typedef struct stack
{
int data[maxsize];
int top;
}stack;
队列的结构体
typedef struct queue
{
int data[maxsize];
int front,rear;
}queue;
1、Q是一个队列,S是一个空栈,编写算法使得队列中元素逆置
草率版本
void reverse(stack &s,queue &q)
{
while(q.front != q.rear)
{
push(s,dequeue(q));
}
while(s.top!=-1)
enqueue(q,pop(s));
}
851版本
stack<int> s;
queue<int> q;
void reverse()
{
while(!q.empty())
{
int temp=q.front();
q.pop();
s.push(temp);
}
while(!s.empty())
{
int temp=s.top();
s.pop();
q.push(temp);
}
}
2、判断单链表的全部 n 个字符是否中心对称
851版本
//已知长度为n
bool judge(Linklist L)
{
LNode *p=L->next;
LNode *q=L->next;
stack<char> s;
while(p!=NULL)//塞入栈
{
s.push(p->data);
p=p->next;
}
for(int i=0;i<n/2;i++)
{
int temp=s.top();
if(q->data != temp)
return false;
s.pop();
q=q->next;
}
return true;
}
3、判断一个表达式中括号是否配对(假设只包含圆括号)
851
bool judge(char txt[],int n)
{
stack<char> s;
//遍历一遍
for(int i=0;i<n,i++)
{
if(txt[i] == '(')
s.push('(');
else if(txt[i]==')')
{
//检查栈
if(s.empty())
return false;
else
s.pop(); //找到匹配的括号了
}
}
if(s.empty())
return true;
else
return false;
}
树
//树的结构体:
typedef struct BTNode
{
char data;
struct BTNode *lchild, *rchild;
} BTNode, *BiTree;
//带初始化函数
struct TreeNode
{
int data;
struct TreeNode *lchild,*rchild;
TreeNode(int x):data(x),lchild(NULL),rchild(NULL){}
};
//使用初始化函数
TreeNode t1=TreeNode(1);
TreeNode t2=TreeNode(2);
TreeNode t3=TreeNode(3);
t1.lchild=&t2;
t1.rchild=&t3;
cout<<"depth="<<depth(&t1);
1.树的层序遍历+分层实现
queue<TreeNode*> que;
vector<vector<int> result;
void fun(TreeNode* T)
{
if(T!=NULL)
que.push(T);
vector<int> vec;
while(!que.empty())
{
int size=que.size();
while(size--)
{
TreeNode *temp=que.front();
que.pop();
vec.push_back(temp->data);
if(temp->lchild)
que.push(temp->lchild);
if(temp->rchild)
que.push(temp->rchild);
}
}
result.push(vec);
}
2.交换树的所有左右孩子结点
void ExchangeChild(TNode* root)
{//交换树的左右孩子
if(root->lchild||root->rchild)//如果存在一个非空孩子,则交换左右孩子
{
TNode *mid=root->lchild;
root->lchild=root->rchild;
root->rchild=mid;
}
if(root->lchild)
{
ExchangeChild(root->lchild);
}
if(root->rchild)
{
ExchangeChild(root->rchild);
}
}
3.双亲表示法做存储结构,求树的深度
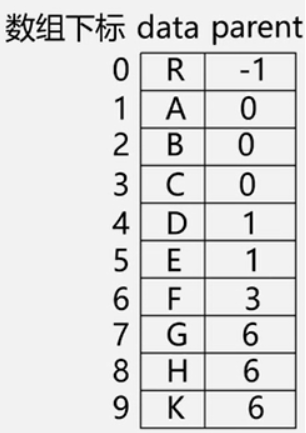
struct node
{
int data;
int parent;
}
以双亲表示法作树的存储结构,对每一结点,找其双亲和双亲的双亲,直至根结点,就可求出每一结点的
层次,取其结点的最大层次就是树的深度。
int maxdepth=0;
void fun(node[],int n)
{
for(int i=1;i<=n;i++)
{
int temp=0,f=i;
while(f>0)
{
temp++;
f=node[f].parent;
}
if(temp>maxdepth)
maxdepth=temp;
}
}
4.二叉树非递归前、中、后序遍历
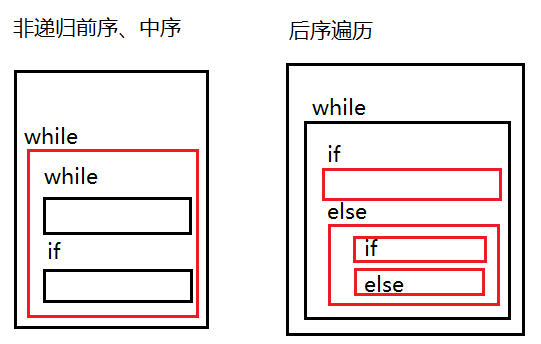
//非递归前序遍历
void preOrder2(BinTree *root)
{
stack<BinTree*> s;
BinTree *p=root;
while(p!=NULL || !s.empty())
{
while(p!=NULL) //往左下一路寻找
{
cout<<p->data<<" ";
s.push(p);
p=p->lchild;
}
if(!s.empty()) //右子树
{
p=s.top();
s.pop();
p=p->rchild;
}
}
}
//非递归中序遍历
void InOrder(TreeNode *root)
{
stack<TreeNode*> s;
TreeNode *p=root;
while(p!=NULL || !s.empty())
{
while(p!=NULL) //往左下一路寻找
{
s.push(p);
p=p->left;
}
if(!s.empty()) //右子树
{
p=s.top();
s.pop();
cout<<p->val<<" "; //唯一变动
p=p->right;
}
}
}
//非递归后序遍历
void Postorder(TreeNode *T)
{
stack<TreeNode*> s;
TreeNode *tag=NULL;
while(T!=NULL || !s.empty())
{
if(T!=NULL)
{
s.push(T);
T=T->lchild;//一路往左
}else
{
T=s.top(); //取出最后一个
if(T->rchild && T->rchild != tag)//往右走的通
T=T->rchild;
else
{
T=s.top();
s.pop();
cout<<T->data<<" ";
tag=T;
T=NULL;
}
}
}
}
代码随想录版本
//非递归前序
vector<int> preorder(TreeNode *root)
{
stack<TreeNode*> s;
TreeNode *node;
vector<int> vec;
s.push(root);
while(!s.empty())
{
node=s.top();
s.pop();
if(node!=NULL) vec.push_back(node->data);
else continue;
s.push(node->rchild); //先入栈右孩子,再入栈左孩子,这样出栈的时候就是(中、左、右)
s.push(node->lchild);
}
return vec;
}
//非递归后序
vector<int> postorder(TreeNode *root)
{
stack<TreeNode*> s;
TreeNode *node;
vector<int> vec;
s.push(root);
while(!s.empty())
{
node=s.top();
s.pop();
if(node!=NULL) vec.push_back(node->data);
else continue;
s.push(node->lchild); //先入栈左孩子,再入栈右孩子,这样出栈的时候就是(中、右、左)
s.push(node->rchild);//最后再对(中、右、左)翻转一下得到(左、右、中)
}
reverse(vec.begin(),vec.end()); //对vector进行逆置
return vec;
}
5.算二叉树中所有节点个数
int sum=0;
int count(TreeNode *T,int &sum)
{
if(T==NULL)
return ;
sum++;
count(T->lchild,sum);
count(T->rchild,sum);
}
int count(TreeNode *p)
{
int n1,n2;
if(p==NULL)
return 0;
else
{
n1=count(p->lchild);
n2=count(p->rchild);
return n1+n2+1;
}
}
6.计算所有叶子结点个数
int sum=0;
int count(TreeNode *T,int &sum)
{
if(T==NULL)
return ;
else
{
if(T->lchild==NULL && T->rchild==NULL)
sum++;
count(T->lchild,sum);
count(T->rchild,sum);
}
}
int count(TreeNode *T)
{
int n1,n2;
if(T==NULL)
return 0;
if(!T->lchild && !T->rchild)
return 1;
else
{
n1=count(T->lchild);
n2=count(T->rchild);
return n1+n2;
}
}
7.计算双分支结点个数
int count(TreeNode *T)
{
int n1,n2;
if(T==NULL)
return 0;
if(p->lchild && p->rchild)
{
n1=count(p->lchild);
n2=count(p->rchild);
return n1+n2+1;
}else{
n1=count(p->lchild);
n2=count(p->rchild);
return n1+n2;
}
}
8.计算二叉树深度
int getDepth(TreeNode *p)
{
int LD,RD;
if(p==NULL)
return 0;
else
{
LD=getDepth(p->lchild);
RD=getDepth(p->rchild);
return max(LD,RD)+1;
}
}
9.查找二叉树中data域等于key的结点是否存在,若存在,将q指向它,否则为空
fun(TreeNode *p,TreeNode *&q,int key)
{
//在遍历基础上加一个
if(p->data==key)
q=p;
}
10.求二叉树中,值为x的结点的层号
//求层号加求值
//使用的时候用fun(root,x,1)
void fun(TreeNode *p,char x,int L)
{
if(p==NULL)
return ;
else
{
if(p->data==x)
cout<<"所在层数为"<<L;
fun(p->lchild,x,L+1);
fun(p->rchild,x,L+1);
}
}
11.先序遍历中第k个结点
// int n=0;
// trave(root,2,n);
void trave(TreeNode *p,int k,int &n)
{
if(p==NULL)
return ;
else
{
++n;
if(k==n){
cout<<p->data;
return ;
}
trave(p->lchild,k,n);
trave(p->rchild,k,n);
}
}
12.二叉树中元素为 x 的结点,删除以它为根的子树
void del(TreeNode *&bt,char key)
{
if(bt==NULL)
return ;
else
{
if(bt->data==key){
bt=NULL; //就完成删除了,连同子树一起删除
return;
}
del(bt->lchild,key);
del(bt->rchild,key);
}
}
13.删除二叉排序树的值为x的结点(删完需要重排)
核心思想:已删除某个结点为例,用非递归后序遍历算法调用删除某个结点的函数.
void Delete(BiTree *p)
{ /* 从二叉排序树中删除结点p,并重接它的左或右子树。 */
BiTree *q,*s;
if(!p->rchild) /* 右子树空则只需重接它的左子树(待删结点是叶子也走此分支) */
{
q=p;//用q结点保存p的位置
p=p->lchild;
delete q;
}
else if(!p->lchild) /* 只需重接它的右子树 */
{
q=p;
p=p->rchild;
delete q;
}
else /* 左右子树均不空 */
{
q=p;
s=p->lchild;
while(s->rchild) /* 转左,然后向右到尽头(找待删结点的前驱) */
{
q=s;
s=s->rchild;
}
p->data=s->data; /* s指向被删结点的"前驱"(将被删结点前驱的值取代被删结点的值)*/
if(q!=p)
q->rchild=s->lchild; /* 重接*q的右子树 */
else
q->lchild=s->lchild; /* 重接*q的左子树 */
delete s;
}
}
14.在二叉树中查找值为 x 的结点,打印出值为x的所有祖先
后序遍历就是天然的回溯过程,最先处理的一定是叶子节点。
接下来就看如何判断一个节点是节点q和节点p的公共公共祖先呢。
「如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者 左子树出现结点q,右子树出现节点p,那么该节点就是节点p和q的最近公共祖先。」
使用后序遍历,回溯的过程,就是从低向上遍历节点,一旦发现如何这个条件的节点,就是最近公共节点了。
//后序遍历的改版
void fun(TreeNode *T,char x)
{
stack<TreeNode*> s;
TreeNode *tag=NULL;
while(T!=NULL || !s.empty())
{
if(T!=NULL)
{
s.push(T);
T=T->lchild;
}else
{
T=s.top();
if(T->data=x)//非递归后序遍历中找,找到立马把前面的全部输出干净
while(!s.empty())
{
cout<<s.top();
s.pop();
}
tag=T;
T=NULL;
}
}
}
15.二叉树的最近公共祖先
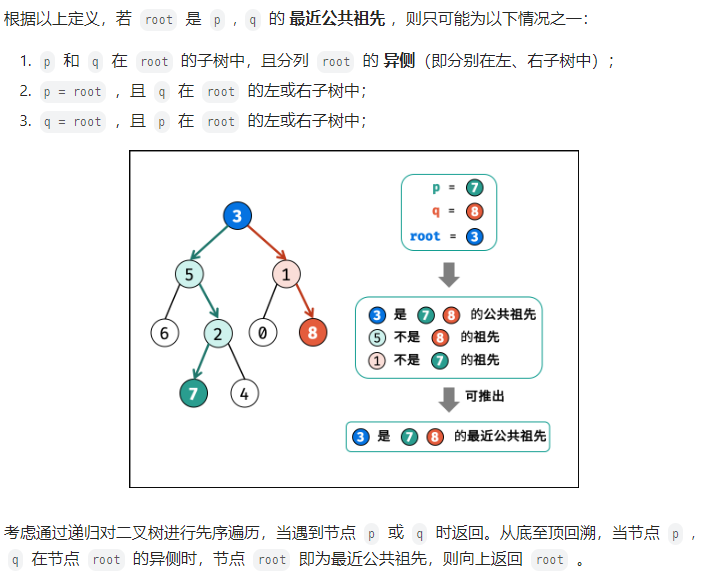

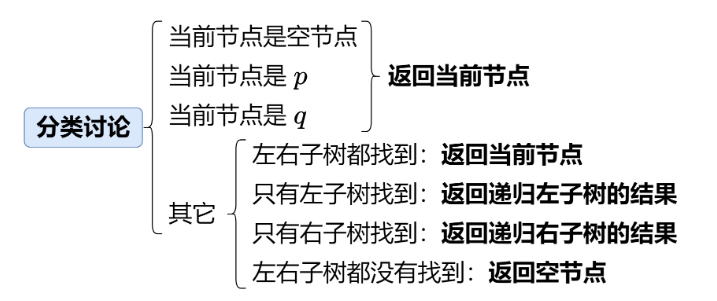
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == NULL || root == p || root == q)
return root;
TreeNode *left = lowestCommonAncestor(root->left, p, q);
TreeNode *right = lowestCommonAncestor(root->right, p, q);
if(left == NULL)
return right;
if(right == NULL)
return left;
return root;
}
16.计算二叉树的带权路径长度(叶子节点)
void fun(TreeNode* T)
{
if(T!=NULL)
que.push(T);
vector<int> vec;
int deep=0;
int wpl=0;
while(!que.empty())
{
int size=que.size();
while(size--)
{
TreeNode *temp=que.front();
que.pop();
if(temp->lchild==NULL && temp->rchild==NULL)//到达叶子结点
wpl+=deep*temp->data;
if(temp->lchild)
que.push(temp->lchild);
if(temp->rchild)
que.push(temp->rchild);
}
deep++;
}
}
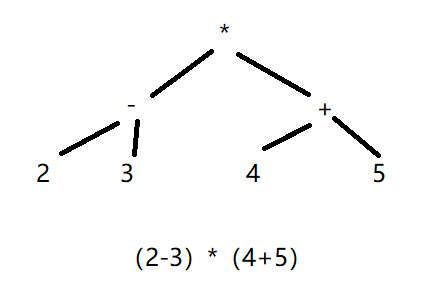
17.将给定二叉树转化为等价中缀表达式
void fun(TreeNode *p,int deep)
{
if(p==NULL)
return ;
else
{
if((p->lchild || p->rchild) && deep>1)
cout<<'(';
if(p->lchild!=NULL)
fun(p->lchild,deep+1);
cout<<p->data;
if(p->rchild!=NULL)
fun(p->rchild,deep+1);
if((p->lchild || p->rchild) && deep>1)
cout<<')';
}
}
巧妙运用中序遍历,实现转化。
注意括号的增加
1.左子树有子树加括号
2.右子树有子树结束加括号
3.根节点不加括号
4.叶子结点不加括号
void BtreeToExp(TreeNode *T,int deep)
{
if(T==NULL){
return ;
}
else if(T->left==NULL&&T->right==NULL){ //叶子结点
cout<<T->data;
}
else{
if(deep>1) cout<<"(";
BtreeToExp(T->left,deep+1);
cout<<T->data;
BtreeToExp(T->right,deep+1);
if(deep>1) cout<<")";
}
}
18.用孩子兄弟表示法求树所有叶子结点个数
//左孩子右兄弟
int fun(TreeNode *p)
{
if(p==NULL)
return 0;
if(p->lchild==NULL)//无孩子——叶子结点
return fun(p->rchild)+1;
return fun(p->rchild)+fun(p->rchild);
}
图
图的存储
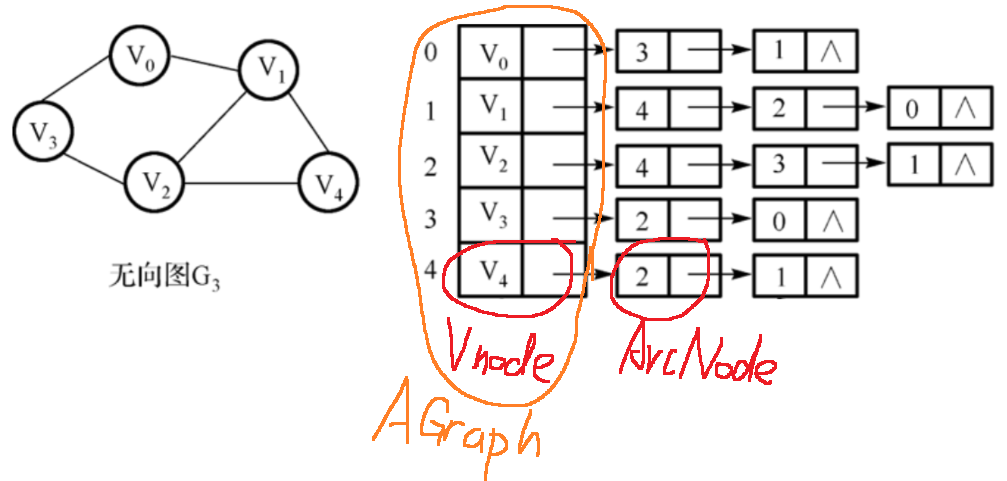
邻接表存储:
struct ArcNode
{
int adjvex; //存储边的另一个顶点 adjList: adj是adjoin的缩写,邻接的意思
struct ArcNode *nextarc;
};
struct Vnode
{
int data;
struct ArcNode *firstarc;
};
struct AGraph
{
Vnode adjlist[maxsize];
int numver, numedg;
};
邻接矩阵存储:
typedef struct
{
char data[maxsize];
int Edge[maxsize][maxsize];
int numver, numedg; //vertex 顶点
} mgraph
图算法 Dijkstra 迪杰斯特拉
void Dijkstra(MGraph &g,int v) //从v结点开始
{
int vis[maxn];//标记数组
int path[maxn];//v到任一结点的前项结点
int dist[maxn];//v到其他顶点的路径长度
//初始化
for(int i=0;i<g->vernum;i++)
{
dist[i]=g->edges[v][i];//v-->其他顶点
vis[i]=0;
if(g->edges[v][i]<Maxn) //v-i之间有路径
path[i]=v;
else
path[i]=-1;
}
vis[v]=1;
path[v]=-1; //顶点v自身
int k; //标记最小值位置
for(int i=1;i<g->vernum;i++)
{
int min =Maxn;
for(int j=0;j<g->vernum;j++)
{
if(dist[j]<min && vis[j]==0)//未访问中找最小的一个
{
min=dist[j];
k=j;
}
}
vis[k]=1;
for(int j=0;j<g->vernum;j++)//更新最短路径
{
if(vis[j]==0 && dist[k]+g->edges[k][j]<dist[j])//从v-k + 从k-j 小于从v-j
{
dist[j]=dist[k]+g->edges[k][j] //更新
path[j]=k;
}
}
}
}
假设中国每个省会与其他所有省会之间都有直达铁路,prim是研究怎么用最短的里程遍历完所有省会,dijkstra是研究从某一个省会(比如昆明)出发到其他各省会的最短路径;可以想象昆明到哈尔滨在prim里是不会直连的因为这个边的权值太大,而在dijkstra里一定是直连的
prim是“用最少的里程连接所有省会”
dijkstra是“两省会最短路径”
Dijkstra——最短路径
prim——最小生成树
代码上非常接近
Dijkstra:vis[]、dist[]、path[]
prim:selected[]、minDist[]、parent[]
图算法 kruskal克鲁斯卡尔(依次加入最小边)
#include<iostream>
#include<algorithm>
using namespace std;
int n,m; //n个点,m条边
int pre[10000];//所有点连通图的标志点
struct edge
{
int from,to;//边左右连接的两个点
int len;//边的权值或者长度
};
edge arr[10000]; //m条边
bool cmp(edge a,edge b)
{
return a.len<b.len;
}
int Find(int x)//找联通图的标志点+压缩路径
{
int flag=x;
while(pre[flag]!=flag)
flag=pre[flag];
int temp;
while(x!=flag)//压缩路径可以省
{
temp=pre[x];
pre[x]=flag;
x=temp;
}
return flag;
}
int main()
{
cin>>n>>m;
for(int i=0;i<m;i++)
cin>>arr[i].from>>arr[i].to>>arr[i].len;
sort(arr,arr+n,cmp);
for(int i=1;i<=n;i++)//初始每个点都是单独联通图
pre[i]=i;
int pFrom,pTo;
int ans=0;
for(int i=0;i<m;i++)
{
pFrom=Find(arr[i].from);//出发点所在连通图
pTo = Find(arr[i].to);
if(pFrom!=pTo) //两个点构不成环
{
ans+=arr[i].len;
pre[pFrom]=pTo;
}
}
cout<<ans<<endl;
return 0;
}
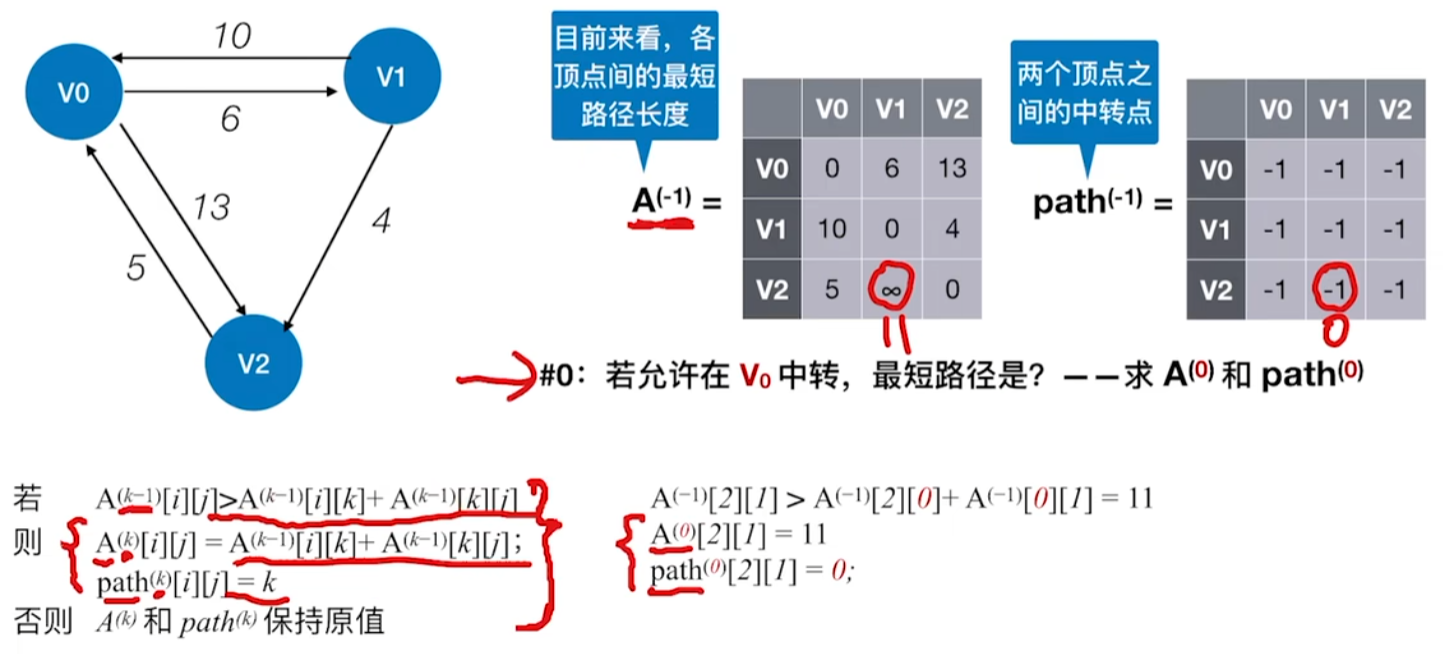
图算法 Floyd算法

类似于在图里使用动态规划思想
求解的是从任意vi--vj的最短路径

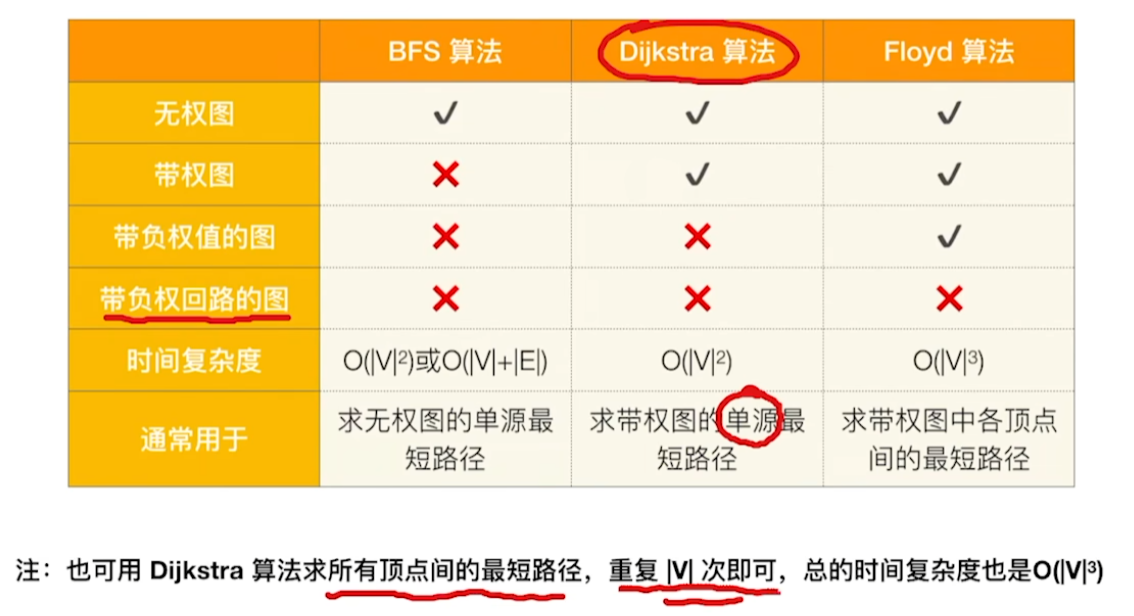
图论总结
1. 邻接表从vi到vj有无路径
int visited[MAX_NUM]={0};
void DFS(AdjList G,int v){//遍历从v
ArcNode *p;
visited[v]=1;//已被访问过
p=G[v].firstarc;
while(p!=NULL){
if(visited[p->adjvex]==0){//若w=p->adjvex 顶点未访问,递归访问它
DFS(G,p->adjvex);
}
p=p->nextarc;//访问过p指向顶点v的下一个邻接点
}
}
int main()
{
cin>>vi>>vj;
if(visit[vj]==1)
cout<<"可以";
else
cout<<"不行"
}
2.图的广度优先和深度优先遍历
bool visited[MaxVerNum];//访问标记数组,用于遍历时的标记
//广度遍历函数 参数:图G,开始结点下标start 作用:宽度遍历
void BFS(Graph G, int start)
{
queue<int> Q;//辅助队列
cout << G.Vex[start];//访问结点
visited[start] = true;
Q.push(start);//入队
while (!Q.empty())//队列非空
{
int v = Q.front();//得到队头元素
Q.pop();//出队
for (int j = 0; j<G.vexnum; j++)//邻接点
{
if (G.Edge[v][j] <INF && !visited[j])//是邻接点且未访问
{
cout << "->";
cout << G.Vex[j];//访问结点
visited[j] = true;
Q.push(j);//入队
}
}
}//while
cout << endl;
}
//深度遍历函数(递归形式)参数:图G,开始结点下标start 作用:深度遍历
void DFS(Graph G, int start)
{
cout << G.Vex[start];//访问
visited[start] = true;
for (int j = 0; j < G.vexnum; j++)
{
if (G.Edge[start][j] < INF && !visited[j])//是邻接点且未访问
{
cout << "->";
DFS(G, j);//递归深度遍历
}
}
}
3.图的深度优先遍历——dfs非递归版本
void dfs(AGraph *g,int v) //基于邻接表的dfs非递归版本
{
ArcNode *p;
stack<int> s;
int i,k;
int visit[maxn];
for(i=0;i<g->vernum;i++)
visit[i]=0;
cout<<g->adjlist[v].data;
visit[v]=1;
s.push(v);
//关键步骤
while(!s.empty())
{
k=s.top();
p=g->adjlist[k].firstarc;
while(p!NULL && visit[p->adjvex]==1)
p=p->nextarc;
if(p==NULL)
s.pop();
else
{
cout<<p->adjvex.data;
visit[p->adjvex]=1;
s.push(p->adjce);
}
}
}
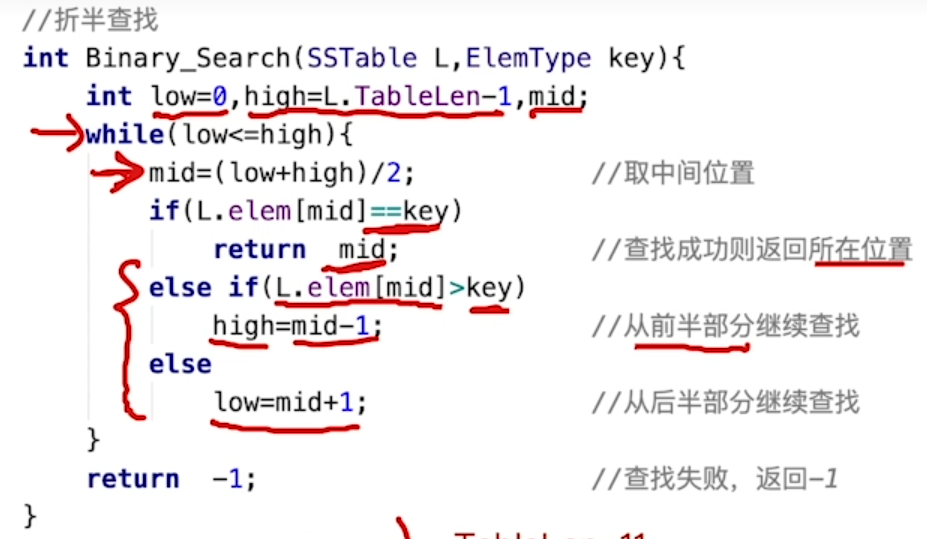
查找
1.折半查找
非递归
递归查找
int arr[maxn];
int n;
int target;
int binary_search(int arr[],int left,int right,int target){
if(left>right)
return -1;
int mid = (left + right) / 2;
if(arr[mid] == target)
return mid;
else if(arr[mid]>target)
return binary_search(arr,left,mid-1,target);
else
return binary_search(arr,mid,right,target);
}
2.分块查找
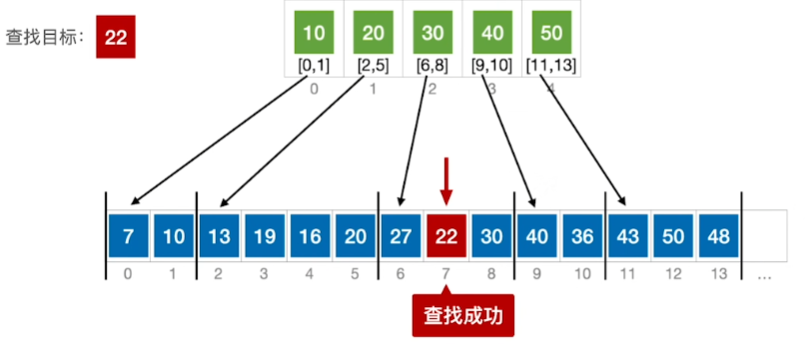
核心思想:把一个完整的数组分成若干块。每一个块存储了这个块的起始位置和结束位置以及每个块中数据的
最大值(块内值的顺序是无序的,块与块之间是按照从小到大排序)。如果我们要用分块查找某个值我们可以先
查找值所在的块(用顺序查找值所在的块也可以折半插入查找),当找出所在的块再用依次顺序查找即可确定是
否能找到所查找的值.
# 1.块的结构体大家不要忘记
# 2.要进行分块查找先查找元素所在的块,(块与块之间是有序的,可以使用折半查找之类的)
# 3.再从块内用顺序查找
struct indexElem
{
int max;//存储块内的最大值
int low, high;//low表示在原数组中的存储起始下标, high表示在原数组中的结束下标
};
int block_search(indexElem index[], int k, int n, int arr[])//k是需要查找的数字,arr表示原数组,index是结构体类型的索引表 n表示有n块
{
int i=0, j, k;
while((i<n)&&indx[i].max<k)//找到所属的块0--n-1
i++;
if (i>=n)
{
cout<<"not found\n";
return 0;
}
j=index[i].low;//块内的起始下标
while(j<=indx[i].high&&arr[j]!=k)//在块内进行查找
j++;
if(j>index[i].high)
{
cout<<"not found\n";
return 0;
}
else
return j;//返回下标
}
排序算法
1.拓扑排序
核心思想:从入度为0的结点开始删除 判断是否为有向无环图(删除的结点是否为n个)
1.首先将图中入度为0的结点入栈,栈初始为空;
2.当栈非空时栈首元素出栈,访问并且将与此元素相邻顶点的入度减1;(去掉相关的边)
3.当某个顶点在去掉相关边后入度为0,则入栈;
4.重复执行2.3操作并且统计访问顶点个数直到栈空。
struct ArcNode
{
int adjvex; //存储边的另一个顶点
struct ArcNode *nextarc;
};
struct Vnode
{
int data;
int cnt; //入度个数
struct ArcNode *firstarc;
};
struct AGraph
{
Vnode adjlist[maxsize];
int vexnum, arcnum;
};
int Puop(AGraph *G)
{
int n=0;//表示删除顶点的个数
stack<Vode> s;
for(int i=0;i<G->vexnum;i++)
{
if(G->adjlist[i].cnt == 0)
s.push(G->adjlist[i]);//遍历n个顶点,入度为零的入栈
}
ArcNode *p;
while(!s.empty())
{
Vnode *temp=s.top();
s.pop();
n++;
p=temp->firstarc;
while(p!=NULL)//遍历所有的邻接边
{
int j=p->adjvex;
--G->adjlist[k].cnt;//入度-1
if(G->adjlist[k].cnt==0)
{
s.push(G->adjlist[k]);
}
p=p->next;
}
}
if(n == G->vexNUm)
return 1;
else
return 0;
}
2.直接插入排序
void Insertsort(int arr[],int n)
{
int i.j;
for(i=2;i<=n;i++)
{
if(arr[i]<arr[i-1])
{
arr[0]=arr[i];
for(j=i-1;arr[j]>arr[0];j--)
{
arr[j+1]=arr[j];
}
arr[j+1]=arr[0];
}
}
}
3.折半插入排序
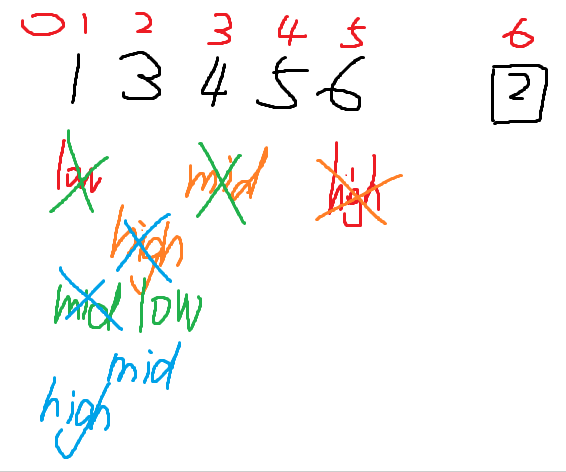
//基于直接插入排序改编
void ZBInsertSort(int A[],int n){
int i,j,high,low,mid;
for(i=2;i<=n;i++){
A[0] = A[i];
low = 1;
high = i-1;
while(low<=high){
mid=(low+high)/2;
if(A[mid]>A[0]){
high=mid-1;
}
else{
low = mid+1;
}
}//while执行完 high+1为需要插入的位置
for(j = i-1;j>=high+1;--j){
A[j+1] = A[j];
}
A[high+1] = A[0];
}
}
4. 堆排序
堆排序利用大根堆
从小到大排序
排到的最大的放在数组末尾,就不会变动了
//以元素k为根的子树进行调整(大根堆)
void HeadAdjust(int a[],int k,int n)
{
a[0] = a[k]; //暂时提出去
for(int i=k*2;i<=n;K*=2)
{
if(i<n && a[i]<a[i+1]) //左右子树找更大的一个
i++;
if(a[i]<a[0])//不用调换
break;
else //需要调换
{
a[k] = a[i];
k=i;
}
}
a[k]=a[0];
}
//建立大根堆
void BuildMaxHeap(int a[],int n){
for(int i=n/2;i>=1;i--){ //除开叶子结点,都要捋一遍
HeadAdjust(a,i,n);
}
}
//堆排序
void HeapSort(int a[],int n){
BuildMaxHeap(a,n);
for(int i=n;i>1;i--){
swap(a[i],a[1]); //把第i个放到a[1]
HeadAdjust(a,1,i-1); //以a[1]为大根堆 调整
}
}
5.希尔排序
//希尔排序
//往后逐个对比
void ShellSort(int A[],int n){
int d,i,j;
for(d = n/2;d>=1;d = d/2){
for(i=d+1;i<=n;++i){
if(A[i]<A[i-d]){
A[0] = A[i];
for(j=i-d;j>0 && A[0]<A[j];j-=d)
A[j+d] = A[j];
A[j+d] = A[0];
}
}
}
}
//希尔排序
//一串捋直了再下一串
void testShellSort(int A[],int n){
int d,i,j;
for(d = n/2;d>=1;d=d/2){ //步长变化
for(i=1;i<=d;i++){ //多少组
for(i=d+1;i<=n;i+=d){ //遍历每一组的所有数字
if(A[i] < A[i-d]){
A[0] = A[i]; //小的放在A[0]
for(j=i-d;j>0 && A[0]<A[j];j-=d){
A[j+d] = A[j];
}
A[j+d] = A[0];
}
}
}
}
}
//插入排序的复杂度都是O(n^2)
int main(){
int A[] = {NULL,49,38,65,97,76,13,27,49};
for(int i = 1;i<MaxSize;i++){
cout<<A[i];
}
testShellSort(A,8);
for(int i = 1;i<MaxSize;i++){
cout<<A[i];
}
return 0;
}
6.冒泡排序
//最简单版冒泡
void BubbleSort(int A[],int n)
{
for(int i=0;i<n;i++)
{
for(int j=n-1;j>1;j--)
{
if(A[j-1] > A[j])
swap(A[j-1],A[j]);
}
}
}
//王道版
void BubbleSort(int A[],int n){
for(int i=0;i<n-1;i++){ //交换的趟数 = n-1
bool flag = false; //表示本趟冒泡是否发生交换的标志
for(int j=n-1;j>i;j--){ //一趟冒泡
if(A[j-1] > A[j]){ //若为逆,则交换
swap(A[j-1],A[j]);
flag = true;
}
}
if(flag == false){ //本趟遍历之后如果没有发生交换,则已经有序
break;
}
}
}
7.快速排序
//Partition (分割)
int Partition(int A[],int low,int high){
int pivot = A[low]; //pivot:枢轴
while(low < high){
while(low<high && A[high] >=pivot) --high; //high前推找比pivot小的
A[low] = A[high];
while(low<high && A[low] <=pivot) ++low; //low后推找比pivot大的
A[high] = A[low];
}
A[low] = pivot;
return low;
}
void QuickSort(int A[],int low,int high){
if(low<high){ //递归跳出的条件
int pivotpos = Partition(A,low,high); //划分
QuickSort(A,low,pivotpos-1); //划分左子表
QuickSort(A,pivotpos+1,high); //划分右子表
}
}
8.简单选择排序
//王道版 简单选择排序
void SelectSort(int A[],int n){
for(int i=0;i<n-1;i++){ //一共排n-1趟
int min = i; //记录最小元素位置
for(int j=i+1;j<n;j++)
if(A[j]<A[min])
min=j; //更新最小元素位置
if(min != i)
swap(A[i],A[min]);
}
}
9.归并排序
int n,a[1000],b[1000];
void merge(int a[],int low,int mid,int high)
{
int i=low,j=mid+1,k=low;
while (i<=mid && j<=high)
{
if (a[i]<a[j])
b[k++]=a[i++];
else
b[k++]=a[j++];
}
while (i<=mid)
b[k++]=a[i++];
while (j<=high)
b[k++]=a[j++];
for (int i=low;i<=high;i++)
a[i]=b[i];
}
void mergesort(int a[],int low,int high)
{
if (low>=high)
return;
int mid=(low+high)/2;
mergesort(a,low,mid);
mergesort(a,mid+1,high);
merge(a,low,mid,high);
}
后缀表达式计算
思路:遍历后缀表达式字符串,如果遇到数字就直接入栈,如果遇到操作符,先出栈第一个数字设为b,再出栈第二个元素设为a,计算 a 操作符 b(a+b或a-b或a*b或a/b),再将结果入栈。直到遍历完表达式,栈中元素为结果。
double op(int a,char Op,int b) //op函数实现 a Op b
{
if(Op=='+') return a+b;
if(Op=='-') return a-b;
if(Op=='*') return a*b;
if(Op=='/')
{
if(b==0)
{
cout<<"Error"<<endl;
return 0;
}
return a*1.0 / (b*1.0);
}
}
int fun(char exp[])
{
int len = strlen(exp);
stack<double> s;
for(int i=0;i<len;i++)
{
if(exp[i]>='0'&&exp[i]<='9')
s.push(exp[i]-'0');
else
{
double a,b,c;
b = s.top();s.pop();
a = s.top();s.pop();
c = op(a,exp[i],b); //调用操作函数,将结果赋值给c
s.push(c);//操作结果入栈
}
}
return s.top();//最后栈顶剩的元素就是结果
}
文件处理(预防考试偷鸡)

#include<fstream>
写入文件
使用流插入运算符( << )向文件写入信息,就像使用该运算符输出信息到屏幕上一样。唯一不同的是,在这里您使用的是 ofstream 或 fstream 对象,而不是 cout 对象。
读取文件
使用流提取运算符( >> )从文件读取信息,就像使用该运算符从键盘输入信息一样。唯一不同的是,在这里您使用的是 ifstream 或 fstream 对象,而不是 cin 对象。
读取 & 写入实例
下面的 C++ 程序以读写模式打开一个文件。在向文件 afile.dat 写入用户输入的信息之后,程序从文件读取信息,并将其输出到屏幕上:
#include <fstream>
#include <iostream>
using namespace std;
int main ()
{
char data[100];
// 以写模式打开文件
ofstream outfile;
outfile.open("afile.dat");
cout << "Writing to the file" << endl;
cout << "Enter your name: ";
cin.getline(data, 100);
// 向文件写入用户输入的数据
outfile << data << endl;
cout << "Enter your age: ";
cin >> data;
cin.ignore();
// 再次向文件写入用户输入的数据
outfile << data << endl;
// 关闭打开的文件
outfile.close();
// 以读模式打开文件
ifstream infile;
infile.open("afile.dat");
cout << "Reading from the file" << endl;
infile >> data;
// 在屏幕上写入数据
cout << data << endl;
// 再次从文件读取数据,并显示它
infile >> data;
cout << data << endl;
// 关闭打开的文件
infile.close();
return 0;
}