abc290g O(TD)算法

前言

似乎洛谷上的题解和AT官方都给的 \(O(TD^2)\) 算法？

这里给出乱搞搞出的一种 \(O(TD)\) 算法。

题解

首先发现 \(D\) 虽然没给出固定上界，但显然不超过 \(log_2 10^{18}=60\)。

再接下来可以发现删边等价于先选一颗子树，再删掉这颗子树内部的子树。

先纸上瞎画两下，发现子树内部全保留或全删除一定比有些保留有些删除优。

因此我们先猜测答案一定是非常左偏的，例如这样。

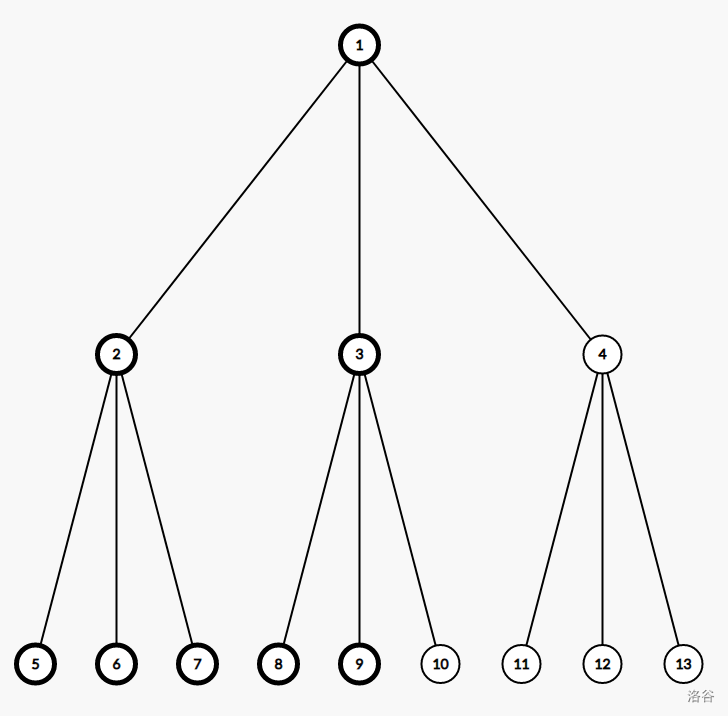
（图中外框深色的即为被选中的）

所以我们可以胡出一种看起来很对的做法：预处理所有深度子树的大小，找到比要求节点数大的最深子树，然后在上面拆。

但是很显然这个结论是不对的那你讲它干嘛

考虑对于这种构造方案的hack，一颗深度是4的满二叉树，选5个点。

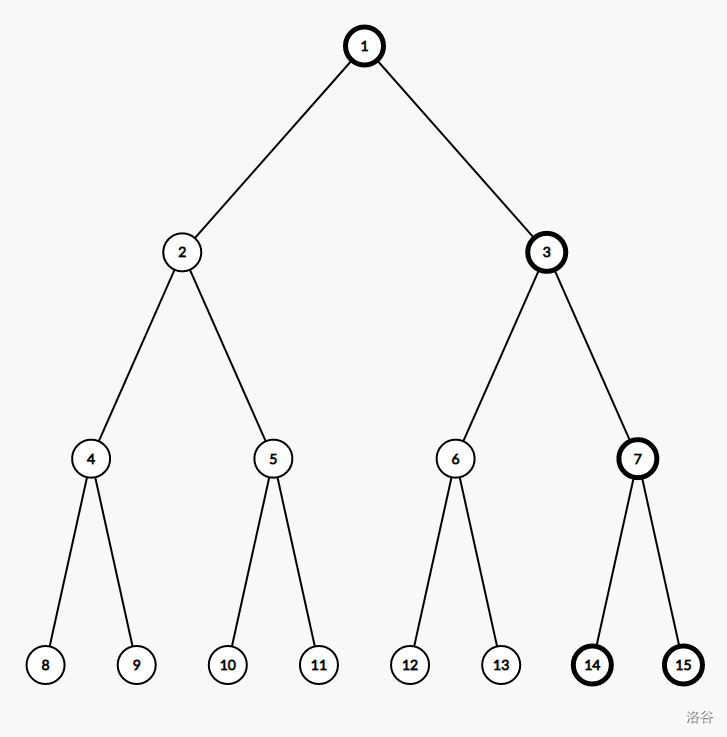
选择方案显然并不是选子树，因为到根节点可以少掉整颗树根往上的边，因此先选一条从根到底部的路径，再选子树更优。

因此我们对这两种情况分讨取 \(\min\) 即可。

时间复杂度 \(O(TD)\)，所有的点都可以在 1ms 内通过。

Code

#include <bits/stdc++.h>
using namespace std;
#define LL long long
LL n,i,j,k,m,t;
LL val[1005];
int main() {
	scanf("%lld",&t);
	while(t--){
		scanf("%lld%lld%lld",&m,&n,&k);
		LL sum=1;
		memset(val,0,sizeof(val));
		val[0]=1;
		for(i=1;i<=m;i++){
			sum*=n;
			val[i]=val[i-1]+sum;
		}
		bool flag=false;
		for(i=m;i>=0;i--)
		  if(k==val[i]){
		  	flag=true;
		  	if(i==m) printf("0\n"); 
		  	else printf("1\n");
		  	break;
		  }
		if(flag==true) continue;
		LL ans=0,tmp=0,num=k;
		for(i=m;i>=0;i--)
		  if(k/val[i]>0){
		  	tmp=i;
		  	break;
		  }
		k--;
		if(tmp!=m-1)ans++;
		for(i=tmp;i>=0;i--){
			LL num1=k/val[i];
			k-=num1*1ll*val[i];
			ans+=(n-num1-1);
			if(k==0){
				ans++;
				break;
			}
			else k--;
		}
		if(num-(m-tmp)<=val[tmp]) tmp--;
		if(tmp<0){
			printf("%lld\n",ans);
			continue;
		}
		num-=(m-tmp);
		LL ans1=(n-1)*(m-tmp-1);
		for(i=tmp;i>=0;i--){
			LL num1=num/val[i];
			num-=num1*1ll*val[i];
			ans1+=(n-num1-1);
			if(num==0){
				ans1++;
				break;
			}
			else num--;
		} 
		printf("%lld\n",min(ans,ans1));
	}
	return 0;
}