①排序
所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。排序算法,就是如何使得记录按照要求排列的方法。排序算法在很多领域得到相当地重视,尤其是在大量数据的处理方面。一个优秀的算法可以节省大量的资源。在各个领域中考虑到数据的各种限制和规范,要得到一个符合实际的优秀算法,得经过大量的推理和分析。
⓿ 复杂度
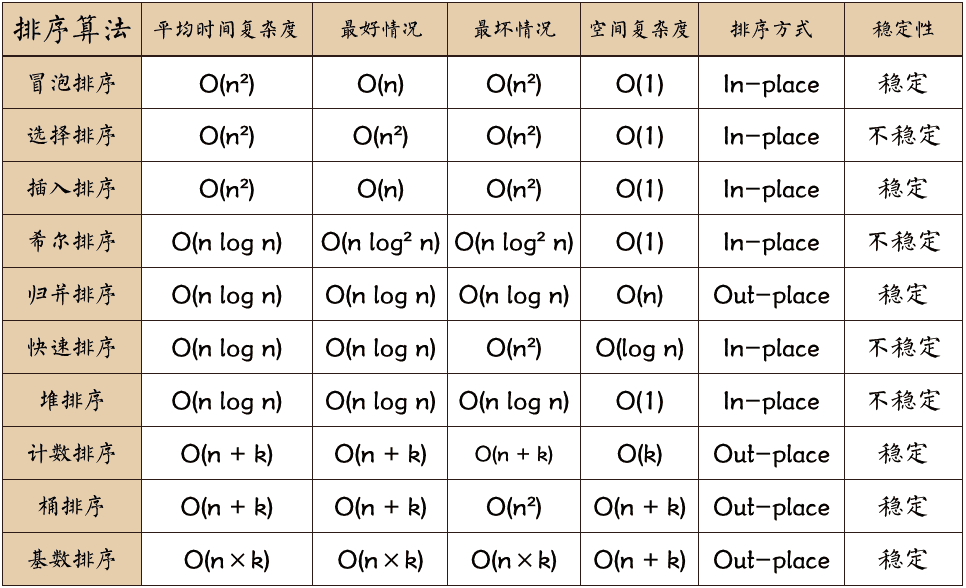
| 排序算法 | 平均时间 | 最差时间 | 稳定性 | 空间 | 备注 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n2) | O(n2) | 稳定 | O(1) | n较小时好 |
| 选择排序 | O(n2) | O(n2) | 不稳定 | O(1) | n较小时好 |
| 插入排序 | O(n2) | O(n2) | 稳定 | O(1) | 大部分已有序时好 |
| 希尔排序 | O(nlogn) | O(ns)(1<s<2) | 不稳定 | O(1) | s是所选分组 |
| 快速排序 | O(nlogn) | O(n2) | 不稳定 | O(logn) | n较大时好 |
| 归并排序 | O(nlogn) | O(nlogn) | 稳定 | O(n)/O(1) | n较大时好 |
| 基数排序 | O(n*k) | O(n*k) | 稳定 | O(n) | n为数据个数,k为数据位数 |
| 堆排序 | O(nlogn) | O(nlogn) | 不稳定 | O(1) | n较大时好 |
| 桶排序 | O(n+k) | O(n2) | 稳定 | O(n+k) | |
| 计数排序 | O(n+k) | O(n+k) | 稳定 | O(k) |
❶冒泡排序
算法步骤
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素作同样的工作。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
- 一共进行了
数组元素个数-1次大循环,小循环要比较的元素越来越少。 - 优化:如果在某次大循环,发现没有发生交换,则证明已经有序。
public class BubbleSort {
public static void main(String[] args) {
int[] arr = {4, 5, 1, 6, 2};
int[] res = bubbleSort(arr);
System.out.println(Arrays.toString(res));
}
public static int[] bubbleSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
boolean flag = true; //定义一个标识,来记录这趟大循环是否发生了交换
for (int j = 0; j < arr.length - i; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
flag = false;
}
}
//如果这次循环没发生交换,直接停止循环
if (flag){
break;
}
}
return arr;
}
}
❷选择排序
算法步骤
- 遍历整个数组,找到最小(大)的元素,放到数组的起始位置。
- 再遍历剩下的数组,找到剩下元素中的最小(大)元素,放到数组的第二个位置。
- 重复以上步骤,直到排序完成。
- 一共需要遍历
数组元素个数-1次,当找到第二大(小)的元素时,可以停止。这时最后一个元素必是最大(小)元素。
public class SelectSort {
public static void main(String[] args) {
int[] arr = {3, 1, 6, 10, 2};
int[] res = selectSort(arr);
System.out.println(Arrays.toString(res));
}
public static int[] selectSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int min = i;
for (int j = i + 1; j < arr.length; j++) {
if(arr[min] > arr[j]){
min = j;
}
}
// 将找到的最小值和i位置所在的值进行交换
int temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
}
return arr;
}
}
❸插入排序
算法步骤
- 将待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
- 从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面)

黑色代表有序序列,红色代表待插入元素
public class InsertSort {
public static void main(String[] args) {
int[] arr = {3, 1, 6, 10, 2};
int[] res = insertSort(arr);
System.out.println(Arrays.toString(res));
}
public static int[] insertSort(int[] arr) {
//从数组的第二个元素开始选择合适的位置插入
for (int i = 1; i < arr.length; i++) {
//记录要插入的数据,后面移动元素可能会覆盖该位置上元素的值
int temp = arr[i];
//从已经排序的序列最右边开始比较,找到比其小的数
//变量j用于遍历前面的有序数组
int j = i;
while (j > 0 && temp < arr[j - 1]) {
//如果有序数组中的元素大于temp,则后移一个位置
arr[j] = arr[j - 1];
j--;
}
//j所指位置就是待插入的位置
if (j != i) {
arr[j] = temp;
}
}
return arr;
}
}
❹希尔排序
插入排序存在的问题
当最后一个元素为整个数组的最小元素时,需要将前面的有序数组中的每个元素都向后移一位,这样是非常花时间的。所以有了希尔排序来帮我们将数组从无序变为整体有序再变为有序。
算法步骤
- 选择一个增量序列 t1(一般是数组长度/2),t2(一般是一个分组长度/2),……,tk,其中 ti > tj, tk = 1;
- 按增量序列个数 k,对序列进行 k 趟排序;
- 每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。当增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。

public class ShellSort {
public static void main(String[] args) {
int[] arr = {3, 6, 1, 4, 5, 8, 2, 0};
int[] res = shellSort(arr);
System.out.println(Arrays.toString(res));
}
public static int[] shellSort(int[] arr) {
//将数组分为gap组,每个组内部进行插入排序
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
//i用来指向未排序数组的首个元素
for (int i = gap; i < arr.length; i++) {
int temp = arr[i];
int j = i;
while (j - gap >= 0 && temp < arr[j - gap]) {
arr[j] = arr[j - gap];
j -= gap;
}
arr[j] = temp;
}
}
return arr;
}
}
❺快速排序
算法步骤
- 先把数组中的一个数当做基准数(pivot),一般会把数组中最左边的数当做基准数。
- 然后从两边进行检索。
- 先从右边检索比基准数小的
- 再从左边检索比基准数大的
- 如果检索到了,就停下,然后交换这两个元素。然后再继续检索
- 直到两边指针重合时,把基准值和重合位置值交换
- 排序好后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 然后递归地(recursive)把小于基准值的子数组和大于基准值元素的子数组再排序。
你注意最后形成的这棵二叉树是什么?是一棵二叉搜索树
你甚至可以这样理解:快速排序的过程是一个构造二叉搜索树的过程。
但谈到二叉搜索树的构造,那就不得不说二叉搜索树不平衡的极端情况,极端情况下二叉搜索树会退化成一个链表,导致操作效率大幅降低。为了避免出现这种极端情况,需要引入随机性。
public class QuickSort {
public static void main(String[] args) {
int[] arr = {8, 12, 19, -1, 45, 0, 14, 4, 11};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
public static void quickSort(int[] arr, int left, int right) {
//递归终止条件
if (left >= right) return;
//定义数组第一个数为基准值
int pivot = arr[left];
//定义两个哨兵
int i = left;
int j = right;
while (i != j) {
//从右往左找比基准值小的数,找到就停止,没找到就继续左移
while (pivot <= arr[j] && i < j) j--;
//从左往右找比基准值大的数,找到就停止,没找到就继续右移
while (pivot >= arr[i] && i < j) i++;
//两边都找到就交换它们
if (i < j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
//此时,i和j相遇,把基准值和重合位置值交换
arr[left] = arr[i];
arr[i] = pivot;
quickSort(arr, left, i - 1);//对左边的子数组进行快速排序
quickSort(arr, i + 1, right);//对右边的子数组进行快速排序
}
}
private static void sort(int[] nums, int left, int right) {
if (left >= right) {
return;
}
int p = partition(nums, left, right);
sort(nums, left, p - 1);
sort(nums, p + 1, right);
}
public static int partition(int[] arr, int left, int right) {
int pivot = arr[left];//定义基准值为数组第一个数
int i = left;
int j = right;
while (i != j) {
//case1:从右往左找比基准值小的数,找到就停止,没找到就继续左移
while (pivot <= arr[j] && i < j) j--;
//case2:从左往右找比基准值大的数,找到就停止,没找到就继续右移
while (pivot >= arr[i] && i < j) i++;
//将找到的两数交换位置
if (i < j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
arr[left] = arr[i];
arr[i] = pivot;//把基准值放到合适的位置
return i;
}
参考:快速排序法(详解)
❻归并排序
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
算法步骤
- 申请空间,该空间用来存放合并后的序列;
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置;
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
- 重复步骤 3 直到某一指针达到序列尾;
- 将序列剩下的所有元素直接复制到合并序列尾。

分治法
治理阶段
 |
 |
|---|---|
public class MergeSort {
public static void main(String[] args) {
int[] arr = {8, 4, 5, 7, 1, 3, 6, 2};
int[] tmp = new int[arr.length];
mergeSort(arr, 0, arr.length - 1, tmp);
System.out.println(Arrays.toString(arr));
}
//分+治
public static void mergeSort(int[] arr, int left, int right, int[] tmp) {
if(left >= right){
return ;
}
int mid = (left + right) / 2;//中间索引
//向左递归进行分解
mergeSort(arr, left, mid, tmp);
//向右递归进行分解
mergeSort(arr, mid + 1, right, tmp);
//合并(治理)
merge(arr, left, right, tmp);
}
//治理阶段(合并)
public static void merge(int[] arr, int left, int right, int[] tmp) {
int mid = (left + right) / 2;
int i = left; // 初始化i, 左边有序序列的初始索引
int j = mid + 1; //初始化j, 右边有序序列的初始索引
int t = 0; // 指向temp数组的当前索引
//(一)
//先把左右两边(有序)的数据按照规则填充到temp数组
//直到左右两边的有序序列,有一边处理完毕为止
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
tmp[t++] = arr[i++];
} else {
tmp[t++] = arr[j++];
}
}
//(二)
//把有剩余数据的一边的数据依次全部填充到temp
while (i <= mid) {//左边的有序序列还有剩余的元素,就全部填充到temp
tmp[t++] = arr[i++];
}
while (j <= right) {
tmp[t++] = arr[j++];
}
//(三)
//将temp数组的元素拷贝到arr
t = 0;
while (left <= right) {
arr[left++] = tmp[t++];
}
}
}
❼基数排序
基数排序是使用空间换时间的经典算法
算法步骤
- 将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零
- 事先准备10个数组(10个桶),对应位数的 0-9
- 根据每个数最低位值(个位),将数放入到对应位置桶中,即进行一次排序
- 然后从 0-9 个数组/桶,依次,按照加入元素的先后顺序取出
- 以此类推,从最低位排序一直到最高位(个位->十位->百位->…->最高位),循环轮数为最大数位长度
- 排序完成以后, 数列就变成一个有序序列
- 需要我们获得最大数的位数:可以通过将最大数变为String类型,再求得它的长度即可
| 排序过程 | 排序后结果 |
|---|---|
 |
|
 |
|
 |
public class RadixSort {
public static void main(String[] args) {
int[] arr = {53, 3, 542, 748, 14, 214};
radixSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void radixSort(int[] arr) {
//定义一个二维数组,表示10个桶, 每个桶就是一个一维数组
int[][] bucket = new int[10][arr.length];
//为了记录每个桶中存放了多少个数据,我们定义一个数组来记录各个桶的每次放入的数据个数
//比如:bucketElementCounts[0] , 记录的就是 bucket[0] 桶的放入数据个数
int[] bucketElementCounts = new int[10];
//最大位数
int maxLen = getMaxLen(arr);
for (int i = 0, n = 1; i < maxLen; i++, n *= 10) {
//maxLen轮排序
for (int j = 0; j < arr.length; j++) {
//取出每个元素的对应位的值
int digitOfElement = arr[j] / n % 10;
//放入到对应的桶中
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
bucketElementCounts[digitOfElement]++;
}
//按照桶的顺序和加入元素的先后顺序取出,放入原来数组
int index = 0;
for (int k = 0; k < 10; k++) {
//如果桶中,有数据,我们才放入到原数组
int position = 0;
while (bucketElementCounts[k] > 0) {
//取出元素放入到arr
arr[index++] = bucket[k][position++];
bucketElementCounts[k]--;
}
}
}
}
//得到该数组中最大元素的位数
public static int getMaxLen(int[] arr) {
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
//将最大值转为字符串,它的长度就是它的位数
int maxLen = (max + "").length();
return maxLen;
}
}
❽堆排序
给定一个数组:String[] arr = {“S”,”O”,”R”,”T”,”E”,”X”,”A”,”M”,”P”,”L”,”E”}请对数组中的字符按从小到大排序。
实现步骤:
- 1.构造堆;
- 2.得到堆顶元素,这个值就是最大值;
- 3.交换堆顶元素和数组中的最后一个元素,此时所有元素中的最大元素已经放到合适的位置;
- 4.对堆进行调整,重新让除了最后一个元素的剩余元素中的最大值放到堆顶;
- 5.重复2~4这个步骤,直到堆中剩一个元素为止。

public class HeapSort {
public static void main(String[] args) throws Exception {
String[] arr = {"S", "O", "R", "T", "E", "X", "A", "M", "P", "L", "E"};
HeapSort.sort(arr);
System.out.println(Arrays.toString(arr));
}
//判断heap堆中索引i处的元素是否小于索引j处的元素
private static boolean less(Comparable[] heap, int i, int j) {
return heap[i].compareTo(heap[j]) < 0;
}
//交换heap堆中i索引和j索引处的值
private static void exch(Comparable[] heap, int i, int j) {
Comparable tmp = heap[i];
heap[i] = heap[j];
heap[j] = tmp;
}
//根据原数组source,构造出堆heap
private static void createHeap(Comparable[] source, Comparable[] heap) {
//把source中的元素拷贝到heap中,heap中的元素就形成一个无序的堆
System.arraycopy(source, 0, heap, 1, source.length);
//对堆中的元素做下沉调整(从长度的一半处开始,往索引1处扫描)
for (int i = (heap.length) / 2; i > 0; i--) {
sink(heap, i, heap.length - 1);
}
}
//对source数组中的数据从小到大排序
public static void sort(Comparable[] source) {
//构建堆
Comparable[] heap = new Comparable[source.length + 1];
createHeap(source, heap);
//定义一个变量,记录未排序的元素中最大的索引
int N = heap.length - 1;
//通过循环,交换1索引处的元素和排序的元素中最大的索引处的元素
while (N != 1) {
//交换元素
exch(heap, 1, N);
//排序交换后最大元素所在的索引,让它不要参与堆的下沉调整
N--;
//需要对索引1处的元素进行对的下沉调整
sink(heap, 1, N);
}
//把heap中的数据复制到原数组source中
System.arraycopy(heap, 1, source, 0, source.length);
}
//在heap堆中,对target处的元素做下沉,范围是0~range
private static void sink(Comparable[] heap, int target, int range) {
while (2 * target <= range) {
//1.找出当前结点的较大的子结点
int max;
if (2 * target + 1 <= range) {
if (less(heap, 2 * target, 2 * target + 1)) {
max = 2 * target + 1;
} else {
max = 2 * target;
}
} else {
max = 2 * target;
}
//2.比较当前结点的值和较大子结点的值
if (!less(heap, target, max)) {
break;
}
exch(heap, target, max);
target = max;
}
}
}