2023年10月10日
更新于2023年10月10日
一、前言
本栏,为线性DP,题目主要来源日常,目前主要来源于Acwing的提高课。希望以后做到线性DP的题目,也能加进来,不断完善。
二、线性DP
2.1 目前的模型:
- 数字三角形模型
- 最长上升子序列模型
2.2 目前解决的问题:
- 可以解决路径上的各种值。
- 解决多条路径的各种值。
- 最长上升子序列来进行的一些变种问题的求解,如怪盗基德的滑翔翼等。要抽象出来是最长上升子序列模型。
- 用上升、下降序列覆盖数组可用的最小数目
2.3 目前推论:
-
最长下降子序列(需要取等)的数量,等于最长上升(严格上升)子序列的长度。
-
同上可得到,最长上升子序列(需要取等)的数量,等于最长下降(严格下降)子序列的长度。
三、题目实例
1. Acwing1015 摘花生
题目理解
状态表示:f[i][j]表示,走到f[i][j]的方法的所有的集合。
集合属性:最大值
状态转移:f[i][j] += max(f[i - 1][j], f[i][j - 1])(因为只能从上面和左面过来)
代码实现
// 两种可能,从上面来和从左面来
// 集合表示是:走到i,j这个格子的集合
// 属性是: 最大值
// 所以d[i][j] = max(d[i][j] + d[i - 1][j], d[i][j] + d[i][j - 1]);
const int N = 110;
int d[N][N];
void solve()
{
memset(d, 0, sizeof d);
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
cin >> d[i][j];
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
d[i][j] = max(d[i][j] + d[i - 1][j], d[i][j] + d[i][j - 1]);
}
cout << d[n][m] << endl;
return;
}
2. Acwing1018 最低通行费
题目理解
状态表示:f[i][j]表示,走到f[i][j]的方法的所有的集合。
集合属性:最小值
状态转移:
- 当
i != 1 && j != 1时
f[i][j] += max(f[i - 1][j], f[i][j - 1])(因为只能从上面和左面过来)
- 当
i == 1时
f[i][j] = f[i][j - 1](因为第一排只能从左边来)
- 当
j == 1时
f[i][j] = f[i - 1][j](因为只能从上面来)
代码实现
// f[i][j] 表示走到 i、j格子的方案集合
// 属性是min
// d[i][j] = min(d[i][j] + d[i - 1][j], d[i][j] + d[i][j - 1])
// 需要处理一下边界
// 如果是第一行的,只能从左边来
// 如果是第一列的, 只能从上面来
const int N = 110;
int d[N][N], f[N][N];
void solve()
{
memset(f, INF, sizeof f);
int n;
cin >> n;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
cin >> d[i][j];
// 根据定义d[0][j]应该为0
for(int i = 0; i <= n; i++)
d[0][i] = d[i][0] = 0;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
{
if(i != 1 && j != 1)
d[i][j] = min(d[i][j] + d[i - 1][j], d[i][j] + d[i][j - 1]);
else if(i == 1)
d[i][j] += d[i][j - 1];
else if(j == 1)
d[i][j] += d[i - 1][j];
}
cout << d[n][n];
return;
}
3. Acwing1027 方格取数
题目理解
通常我们比较容易想到的是\(f[i1][j1][i2][j2]\)去代表\((1,1)(1,1)开始到(i1, j1)(i2, j2)\)两条路线的最大值,那么最后的最大就是\(f[n][n][n][n]\)在这个模型的基础上我们可以优化一下。为以下:
用一维来枚举当前是第几步\(f[k][i1][i2]\)
什么含义呢?就是走了\(k\)步,我第一条走到了\(i1\)行,第二条走到了\(i2\)行
需要特判的是。因为步数是一定的所以我们的列数可以通过\(k - i\)获得到目前的列数。
但是切记我们的格子只可以走一次,所以我们当两条路同时走到一个格子的时候可不能加两次需要特判。
就是当\(i1 == i2\)的时候。
状态表示:f[k][i][j]表示用了k步走到了第一条走到了第i行和第二条走到了第j行
集合属性:最大值
状态转移:
int t = w[i1][j1];
if(i1 != i2) t += w[i2][j2];
int &x = f[k][i1][i2];
x = max(x, f[k-1][i1-1][i2-1] + t);
x = max(x, f[k-1][i1-1][i2] + t);
x = max(x, f[k-1][i1][i2-1] + t);
x = max(x, f[k-1][i1][i2] + t);
代码实现
const int N = 15;
int f[N * 2][N][N], d[N][N];
int n;
void solve()
{
cin >> n;
int a, b, c;
while(cin >> a >> b >> c){
if(a == 0 && b == 0 && c == 0) break;
d[a][b] = c;
}
for(int k = 2; k <= n * 2; k++) // 走了k步
for(int x1 = 1; x1 <= n; x1++)
for(int x2 = 1; x2 <= n; x2++)
{
int y1= k - x1, y2 = k - x2;
if(y1 >= 1 && y1 <= n && y2 >= 1 && y2 <= n) // 在范围内
{
int t = d[x1][y1];
if(x1 != x2) t += d[x2][y2];
int &x = f[k][x1][x2];
x = max(x, f[k - 1][x1 - 1][x2 - 1] + t);
x = max(x, f[k - 1][x1 - 1][x2] + t);
x = max(x, f[k - 1][x1][x2] + t);
x = max(x, f[k - 1][x1][x2 - 1] + t);
}
}
cout << f[n * 2][n][n];
return;
}
4. Acwing275 传纸条
题目理解
这个题目本质上就和上面的方格取数一样了,我们可以把从A到B看作是,第一条路;从B到A看作是第二条路即可。
代码实现
const int N = 55;
int w[N][N], f[N * 2][N][N];
int n, m;
void solve()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
cin >> w[i][j];
for(int k = 2; k <= n + m; k++)
for(int x1 = 1; x1 <= n; x1++)
for(int x2 = 1; x2 <= m; x2++)
{
int y1 = k - x1, y2 = k - x2;
if(y1 <= n && y1 >= 1 && y2 >= 1 && y2 <= m)
{
int t = w[x1][y1];
if(x1 != x2) t += w[x2][y2]; // 如果不是同一个格子就加起来
int &x = f[k][x1][x2];
x = max(x, f[k - 1][x1 - 1][x2 - 1] + t);
x = max(x, f[k - 1][x1 - 1][x2] + t);
x = max(x, f[k - 1][x1][x2 - 1] + t);
x = max(x, f[k - 1][x1][x2] + t);
}
}
cout << f[n + m][n][m];
return;
}
5. Acwing895 最长上升子序列模型Ⅰ
题目理解
状态表示:f[i]表示以i结尾的最长上升子序列的长度
集合属性:最大值
状态转移:如果\(a[i] > a[j]\)的话存在\(f[i] = max(f[i], f[j] + 1)\)
代码实现
const int N = 1010;
int f[N], a[N];
int n;
void solve()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
int res = 0;
for(int i = 1; i <= n; i++)
{
f[i] = 1;
for(int j = 1; j <= i; j++)
if(a[i] > a[j])
f[i] = max(f[i], f[j] + 1);
res = max(res, f[i]);
}
cout << res;
return;
}
6. Acwing896 最长上升子序列模型Ⅱ
题目理解
用贪心的方法来解:其实就是找,当前的数,是前面的序列中,第几小的数那么最长上升子序列也就是这个。
代码实现
int a[N], p[N];
int n;
void solve()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
int len = 1;
for(int i = 1; i <= n; i++)
{
int l = 1, r = len;
while(l < r)
{
int mid = (l + r + 1) >> 1;
if(p[mid] < a[i]) l = mid;
else r = mid - 1;
}
len = max(len, r + 1);
p[r + 1] = a[i];
}
cout << len - 1;
return;
}
7. Acwing1017 怪盗基德的滑翔翼
题目理解
就是求一个数列的最长上升子序列问题。
用我们的\(f[i]\)代表的是,以第i位结尾的最长的子序列长度。
我们这里的怪盗基德是什么思路呢?
我们把它的这个分成两类
从左往右变为,最长上升子序列。
从右往左变为,最长下降子序列。(但是我们再反一下,其实就是一个最长上升子序列)
所以我们这里只需要把楼房的高度正着存一次,然后再倒着存一次,对两个数组同时做 最长上升子序列
代码实现
const int N = 110;
int a[N], n, d[N];
void solve()
{
memset(d, 0, sizeof d);
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
int res = 0;
for(int i = 1; i <= n; i++) // 正的求一次
{
d[i] = 1;
for(int j = 1; j <= i; j++)
if(a[j] < a[i])
d[i] = max(d[i], d[j] + 1);
res = max(res, d[i]);
}
memset(d, 0, sizeof d);
for(int i = n; i >= 1; i--) // 反的求一次
{
d[i] = 1;
for(int j = n; j >= i; j--)
if(a[j] < a[i])
d[i] = max(d[i], d[j] + 1);
res = max(res, d[i]);
}
cout << res << endl;
return;
}
8. Acwing1014 登山
题目理解
要求出来,在一个序列中从左到右严格上升的子序列长度。我们这个题要的东西是,可以再这个序列中任意选一个点实现这样一个规律。
\(T1<…< Ti > Ti+1 >… > TK(1≤i≤K)\)
然后这个序列长度是最长的。所以我们只需要求出从左到T的子序列长度 + 从右到T的下降子序列长度这二者求和的最大值就是哦我们想要的答案。
代码实现
const int N = 1010;
int a[N], d[N], p[N];
void solve()
{
int n;
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
int res = 0;
for(int i = 1; i <= n; i++)
{
d[i] = 1;
for(int j = 1; j <= i; j++)
if(a[i] > a[j])
d[i] = max(d[i], d[j] + 1);
}
for(int i = n; i >= 1; i--)
{
p[i] = 1;
for(int j = n; j >= i; j--)
if(a[i] > a[j])
p[i] = max(p[i], p[j] + 1);
res = max(res, p[i] + d[i]);
}
cout << res - 1; // 因为选择的山算了两次
return;
}
9. Acwing482 合唱队形
题目理解
这个题思路同上,只是最后的答案并不是长度,而是n - 长度
代码实现
const int N = 110;
int a[N], n, d[N], p[N], res;
void solve()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i <= n; i++)
{
d[i] = 1;
for(int j = 1; j <= i; j++)
if(a[i] > a[j])
d[i] = max(d[i], d[j] + 1);
}
for(int i = n; i >= 1; i--)
{
p[i] = 1;
for(int j = n; j >= i; j--)
if(a[i] > a[j])
p[i] = max(p[i], p[j] + 1);
res = max(res, p[i] + d[i]);
}
cout << n - (res - 1);
return;
}
10. Acwing1012 友好城市
题目理解
但是这个题的难点在于,可以抽象出这个最长上升子序列模型
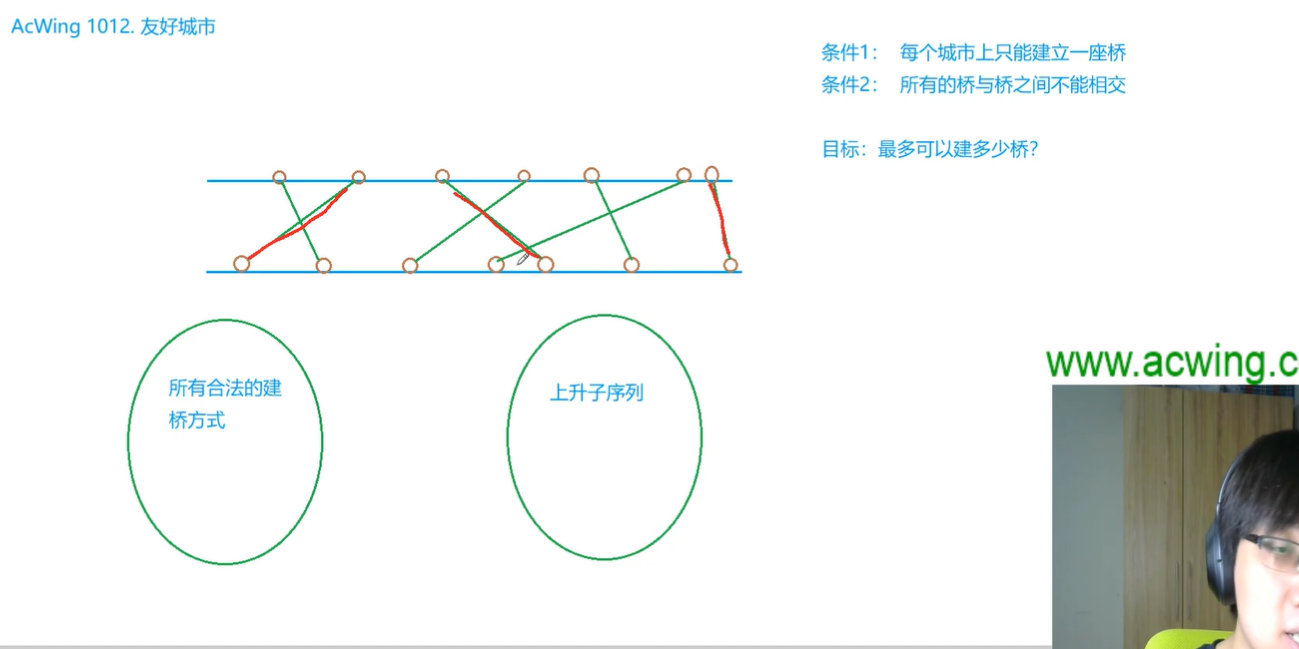
题目重点思路,如何建桥可以不交叉当我们把下半部分排序,得到一个序列后。
如果我们取上半部分的单调上升子序列发现一定一定不会产生交叉!
因为,下半部分是顺序排序,这时我们取上部分的单调上升子序列的话一定不会产生交叉。真的很难想到。
就是当我们只选择最长上升子序列建立点的时候,必定是符合题意得。
说人话就是排序后,因为我是升序的,为了不交叉我也只能选择链接升序的序列
代码实现
const int N = 5010;
int n, res, d[N];
void solve()
{
cin >> n;
vector<PII> a(n);
for(int i = 0; i < n; i++)
cin >> a[i].x >> a[i].y;
sort(a.begin(), a.end());
for(int i = 0; i < n; i++){
d[i] = 1;
for(int j = 0; j < i; j++)
if(a[i].y > a[j].y)
d[i] = max(d[i], d[j] + 1);
res = max(res, d[i]);
}
cout << res;
return;
}
11. Acwing1016 最长上升子序列和
题目理解
这个就比较好想了。
状态表示:f[i]表示以i结尾的最长上升子序列的和
集合属性:最大值
状态转移:如果\(a[i] > a[j]\)的话存在\(d[i] = max(d[i], a[i] + d[j]);\)
代码实现
const int N = 1010;
int a[N], res, n, d[N];
void solve()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i <= n; i++)
{
d[i] = a[i];
for(int j = 1; j <= i; j++)
if(a[i] > a[j])
d[i] = max(d[i], a[i] + d[j]);
res = max(res, d[i]);
}
cout << res;
return;
}
12. Acwing1010 拦截导弹。本题得出结论:序列覆盖问题
题目理解
对于第一问:
翻译过来就是,一门炮最多拦截几枚,那么就是最长不升子序列的长度。
所以直接求一次就好了
对于第二问我们要考虑一下
题目翻译:
翻译过来是,用下降子序列,多少个下降子序列可以把我们的整个数列布满。
然后对于我们这个问题与。最长上升子序列个数是对偶的。就是我们这个的答案等于最长上升子序列。
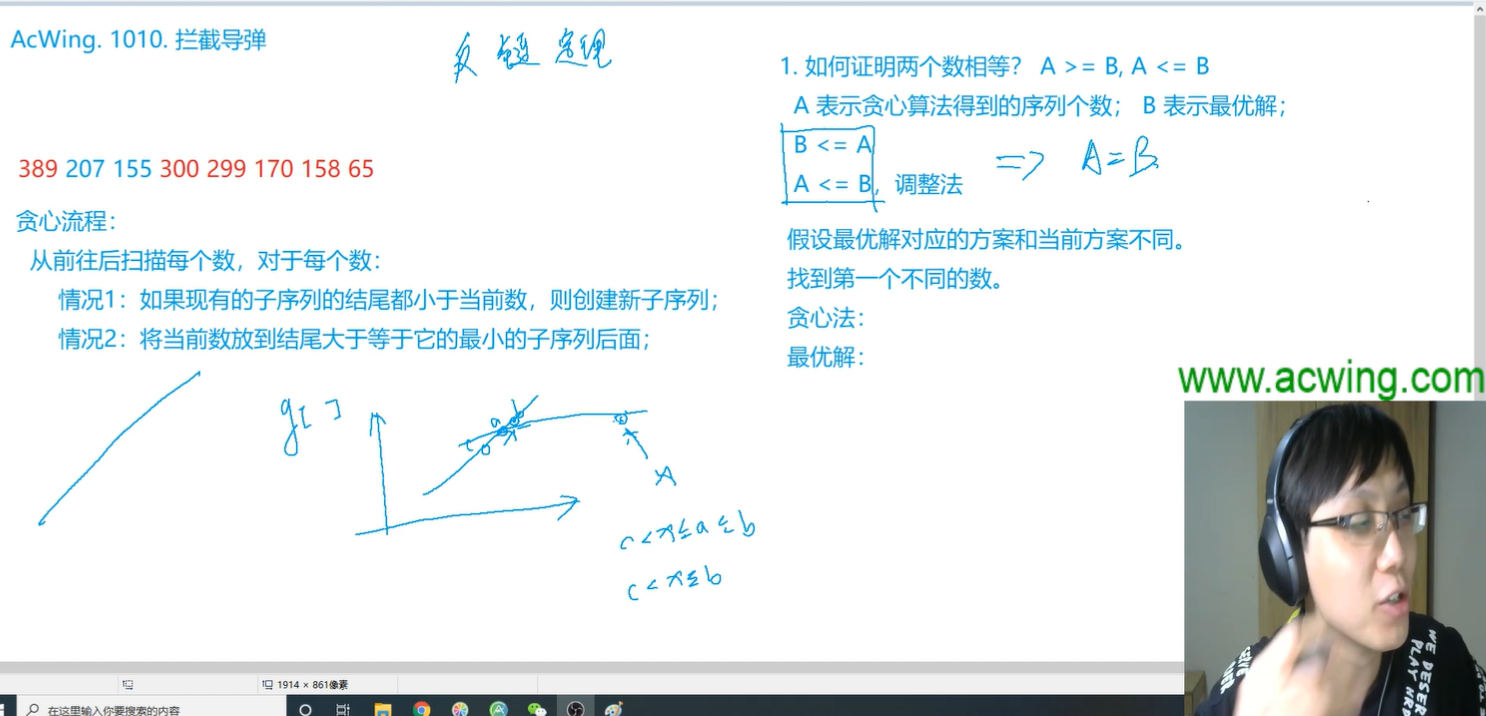
我们从头到尾扫描一次
- 第一种情况是当前这个数是所有子序列结尾的都比他小,就要新开序列
- 第二种是在某一个序列中就已经比它大了,就替换一下
for(int i = 0; i < n; i++)
{
int k = 0;
//从头往后扫描目前的子序列结尾
while(k < cnt && p[k] < a[i]) k++;
//如果目前子序列的结尾都比这个数要小,我就新开一个序列
if(k == cnt)p[cnt++] = a[i];
else p[k] = a[i]; //如果这个数比某个自诩列的结尾要小了,就把这个结尾替换
}
代码实现
贪心版本:
int main()
{
while(cin >> a[n])n++;
int res =0;
//对于第一问就是求一次最长不升子序列
for(int i = 0; i < n; i++)
{
f[i] = 1;
for(int j = 0; j < i ;j++)
{
if(a[i] <= a[j])
f[i] = max(f[i], f[j] + 1);
}
res = max(res, f[i]);
}
cout<<res<<endl;
//对于第二问是贪心思路。(结论等价于求最长上升子序列)
for(int i = 0; i < n; i++)
{
int k = 0;
//从头往后扫描目前的子序列结尾
while(k < cnt && p[k] < a[i]) k++;
//如果目前子序列的结尾都比这个数要小,我就新开一个序列
if(k == cnt)p[cnt++] = a[i];
else p[k] = a[i]; //如果这个数比某个自诩列的结尾要小了,就把这个结尾替换
}
cout<<cnt;
return 0;
}
结论版本:
const int N = 1010;
int a[N], d[N], p[N], res, ind;
void solve()
{
int n = 0;
while(cin >> a[++n]);
for(int i = 1; i < n; i++)
{
d[i] = 1;
for(int j = 1; j < i; j++)
if(a[i] <= a[j])
d[i] = max(d[i], d[j] + 1);
res = max(res, d[i]);
}
for(int i = 1; i < n; i++)
{
p[i] = 1;
for(int j = 1; j <= i; j++)
if(a[j] < a[i])
p[i] = max(p[i], p[j] + 1);
ind = max(p[i], ind);
}
cout << res << endl << ind;
return;
}
13. Acwing187 导弹防御系统
这个题的最原本还是最长上升子序列
题目翻译过来就是用上升序列、下降序列,最少用多少个序列就可以把整个数列覆盖掉
这个题的贪心思想来源于导弹系统题
两个贪心的情况
- 如果比所有的都大就新开序列
- 如果比有比他大的就切换掉
本题的实现
dfs枚举每一种情况使用的个数
#include<iostream>
#include<cstring>
using namespace std;
const int N = 55;
int h[N];
int up[N], down[N];
int res;
int n;
//su 和 sd 就是所用的单调上升和单调下降的使用系统数量
void dfs(int u, int su, int sd)
{
//如果目前使用的系统过多就不要递归了
if (su + sd >= res) return;
//枚举完了
if (u == n)
{
//更新答案
res = min(res, su + sd);
return;
}
//这个思路是从导弹系统题目来的贪心思路
int k = 0;
while (k < su && up[k] >= h[u]) k ++ ; //扫描
if (k < su)
{
//更新一下结尾
int t = up[k];
up[k] = h[u];
dfs(u + 1, su, sd);
up[k] = t;
}
else
{
//添加新的子序列结尾,就相当于多用系统
up[k] = h[u];
dfs(u + 1, su + 1, sd);
}
k = 0;
while (k < sd && down[k] <= h[u]) k ++ ; //扫面
if (k < sd)
{
//更新结尾
int t = down[k];
down[k] = h[u];
dfs(u + 1, su, sd);
//还原现场
down[k] = t;
}
else
{
//添加新的子序列,就多用系统
down[k] = h[u];
dfs(u + 1, su, sd + 1);
}
}
int main()
{
while(cin >> n)
{
if(n == 0)break;
//初始化res
res = n;
for(int i = 0 ; i < n ; i++)
cin >> h[i];
dfs(0, 0, 0);
cout<<res<<endl;
}
return 0;
}