二叉树的存储结构和操作算法
二叉树的存储结构
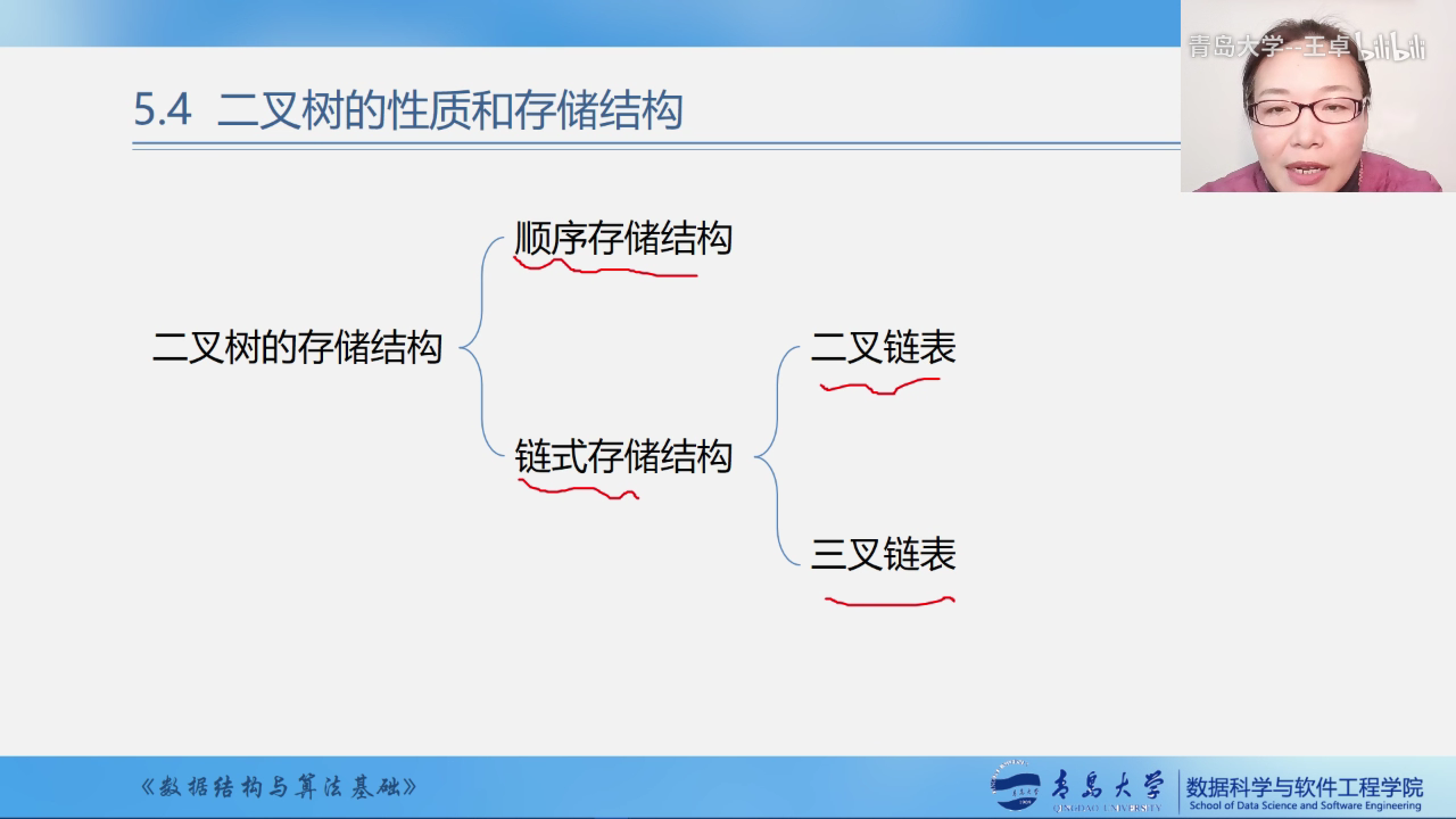
1.顺序存储结构(完全二叉树/满二叉树)
2.链式存储结构(一般二叉树).
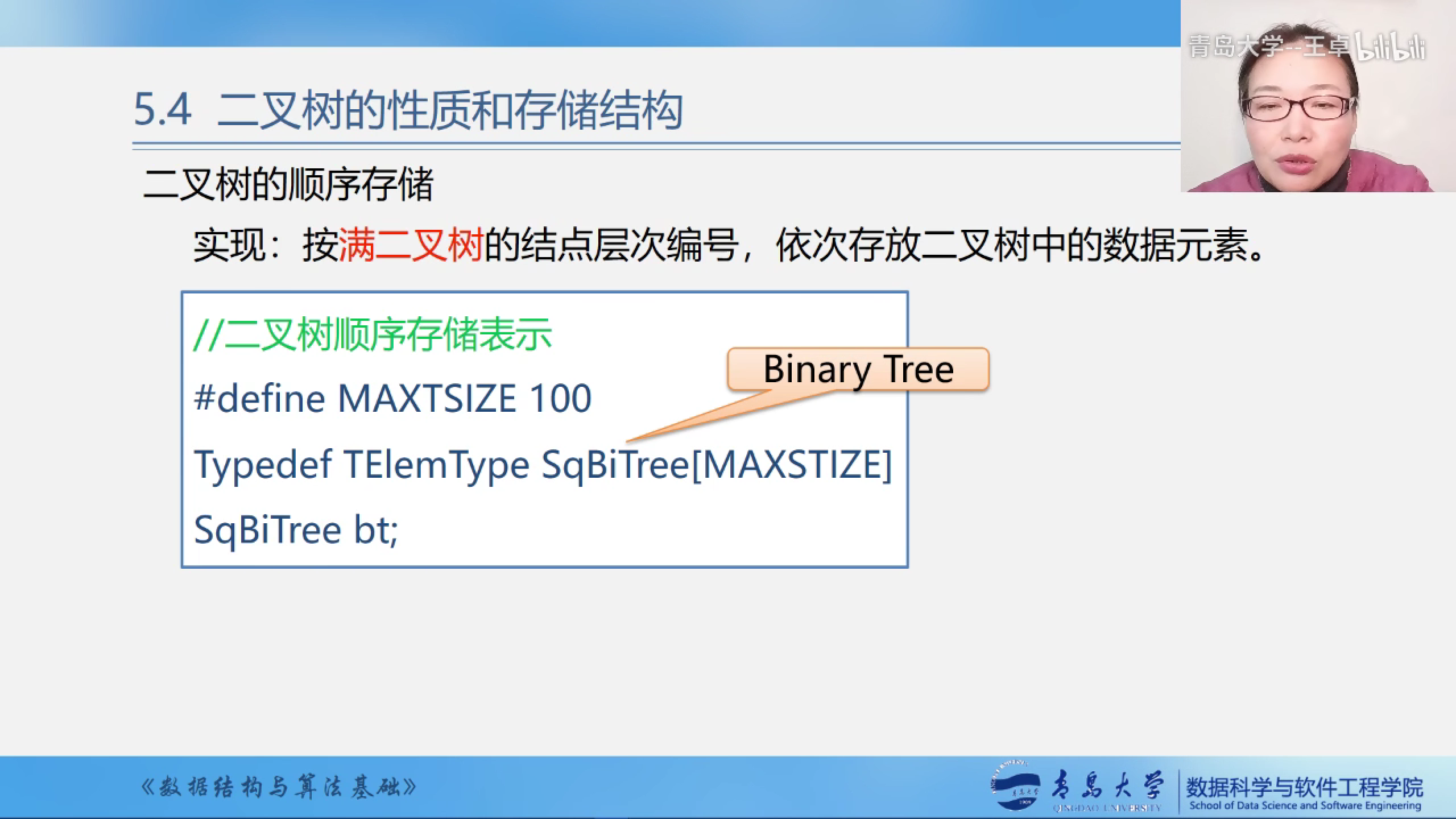
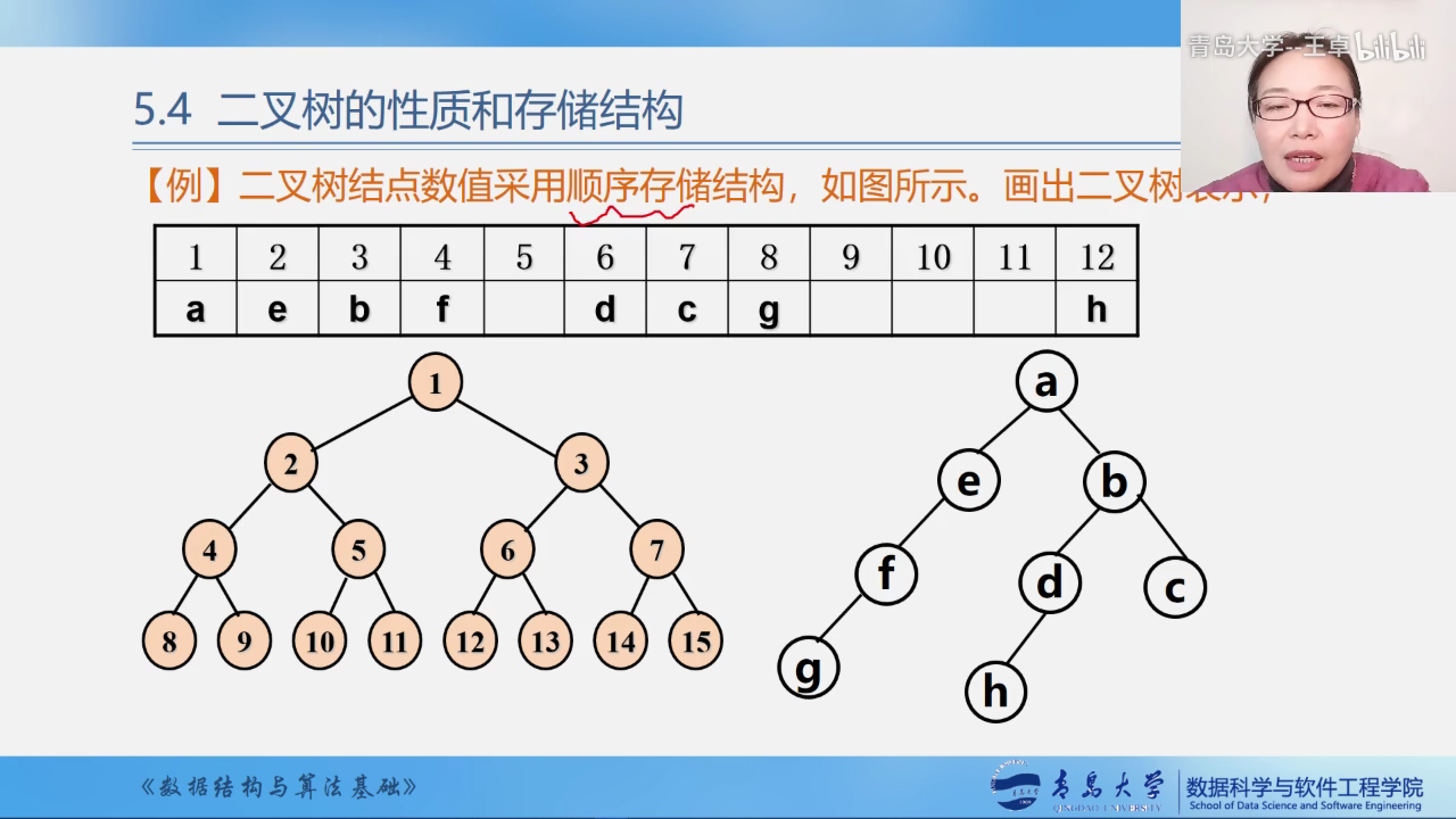
顺序存储结构
按照满二叉树的结点层次编号,然依次后储存在数组当中
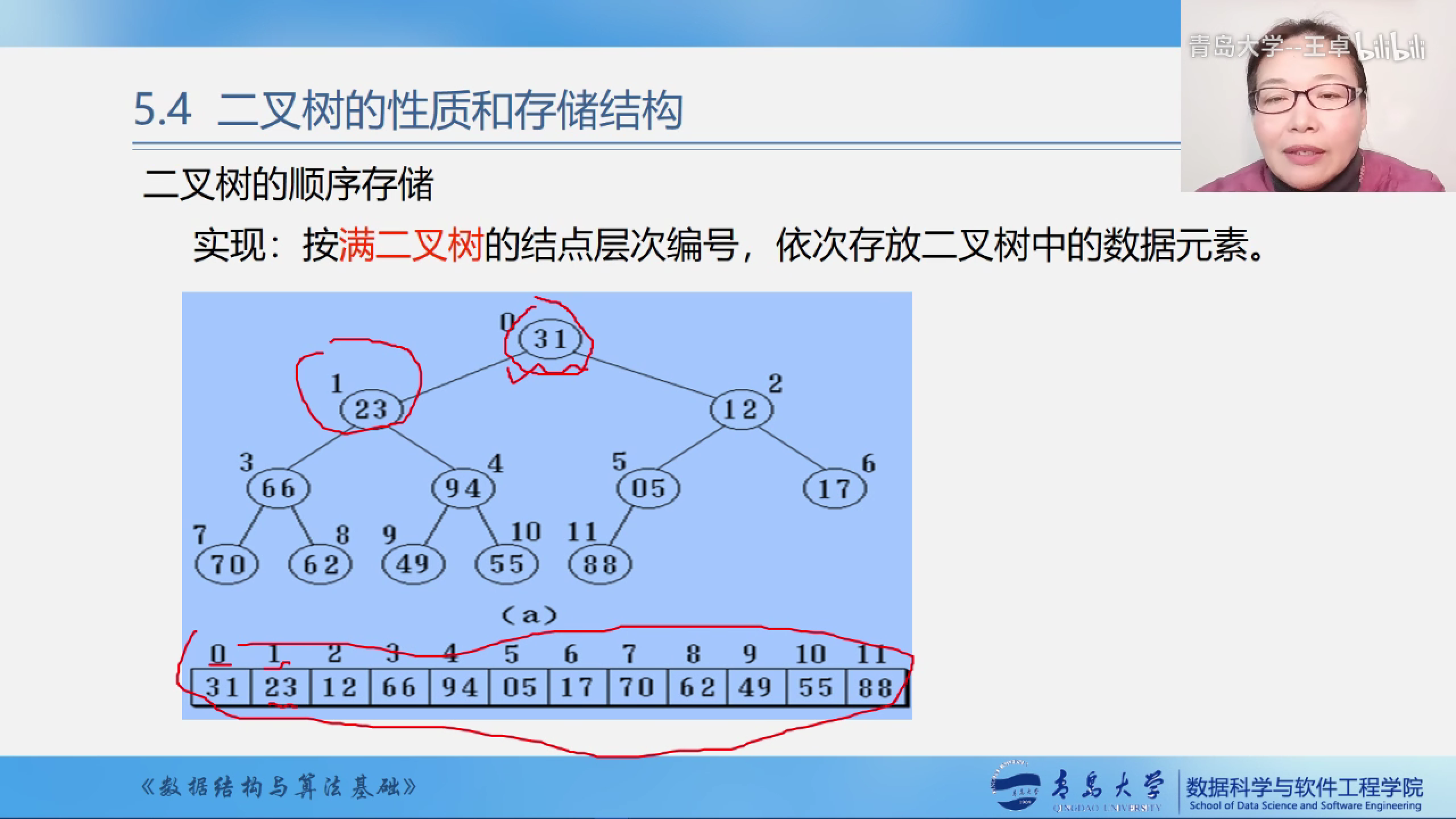
如果该二叉树中位置是空的再对应到数组中的时候就使用0来填充.
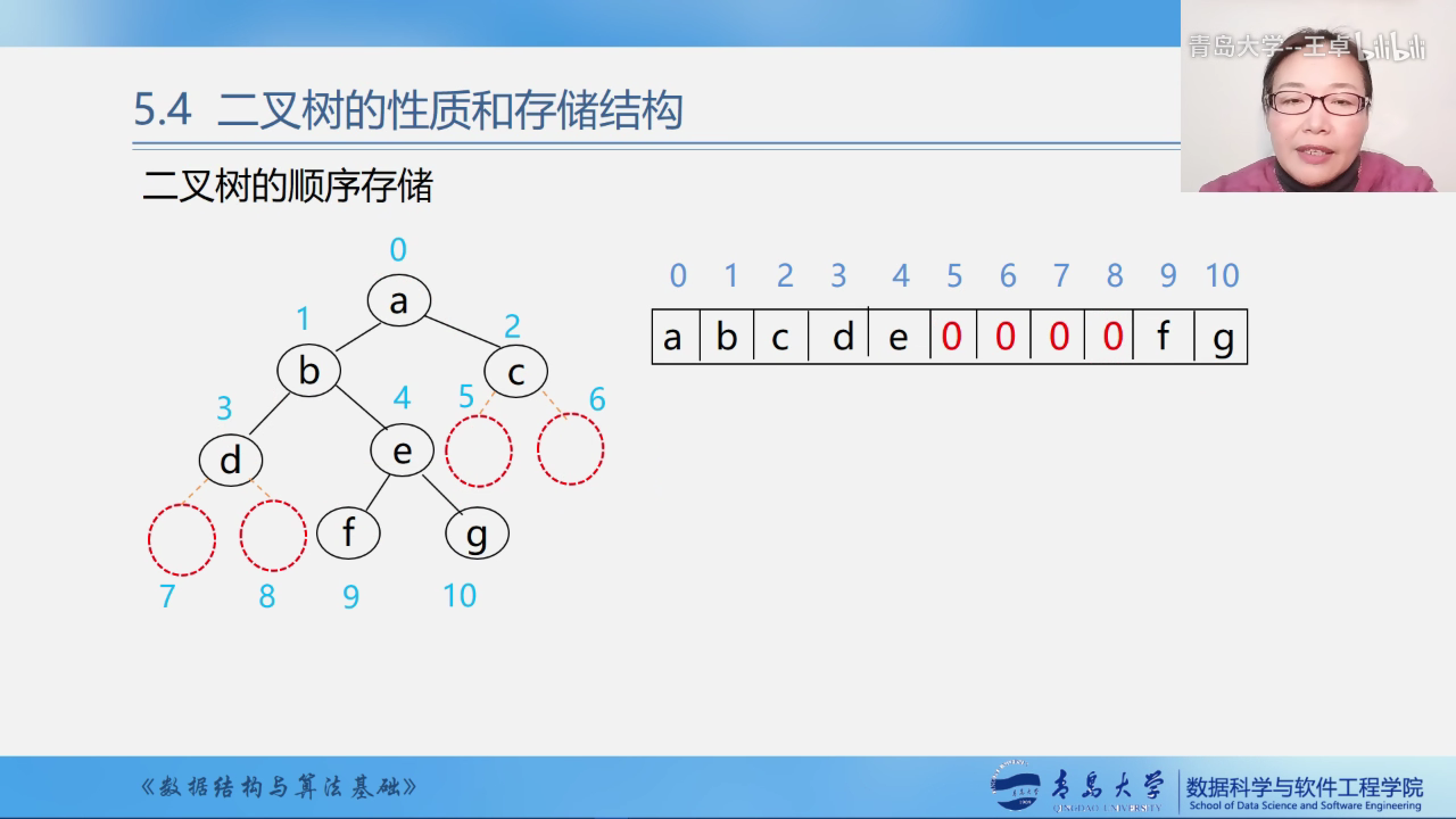
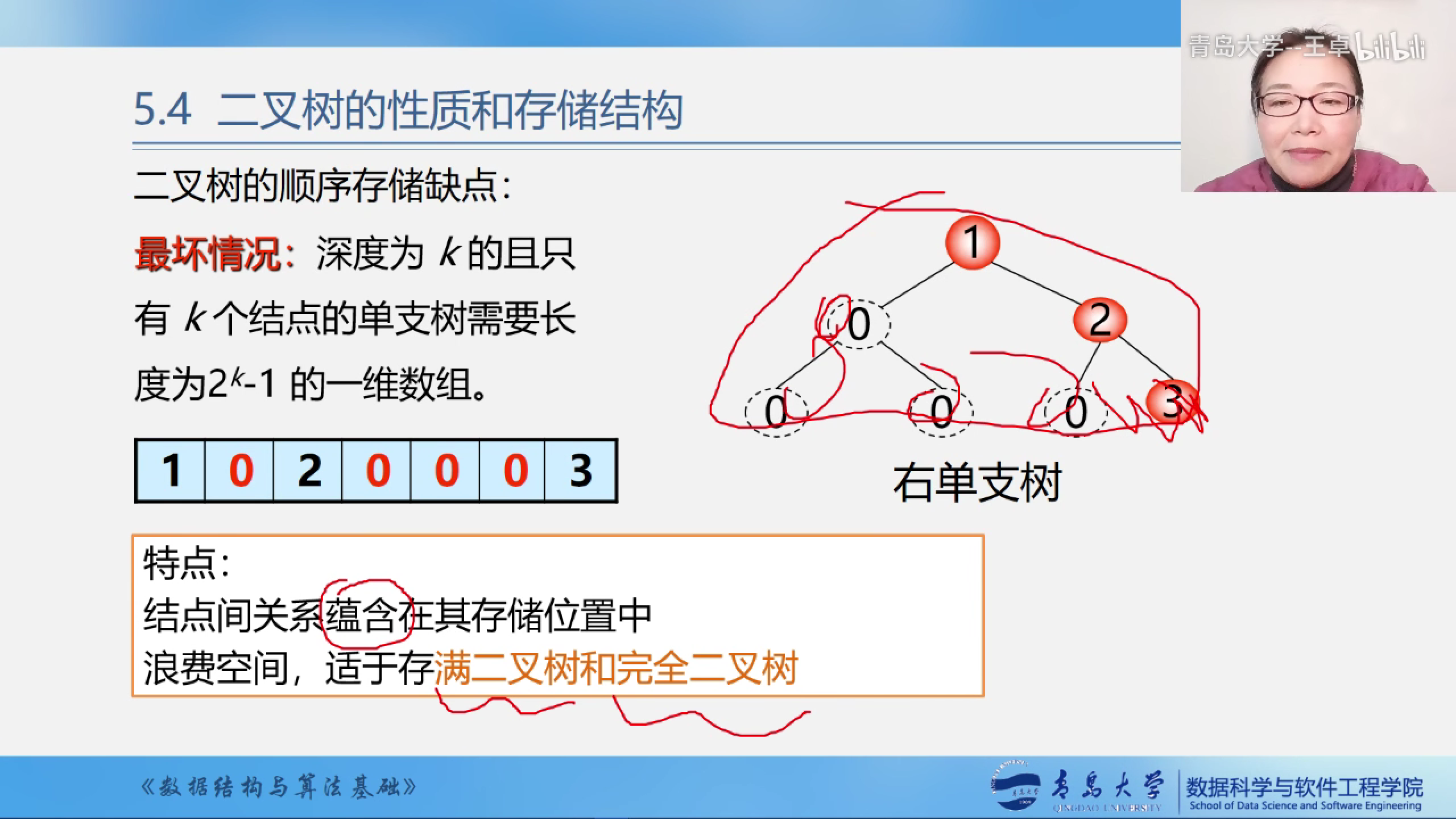
二叉树顺序存储结构的缺点
1.顺序存储结构不能动态的变化
2.如果二叉树退化为右单支树的时候非常浪费空间
所以顺序存储结构适用于满二叉树和完全二叉树
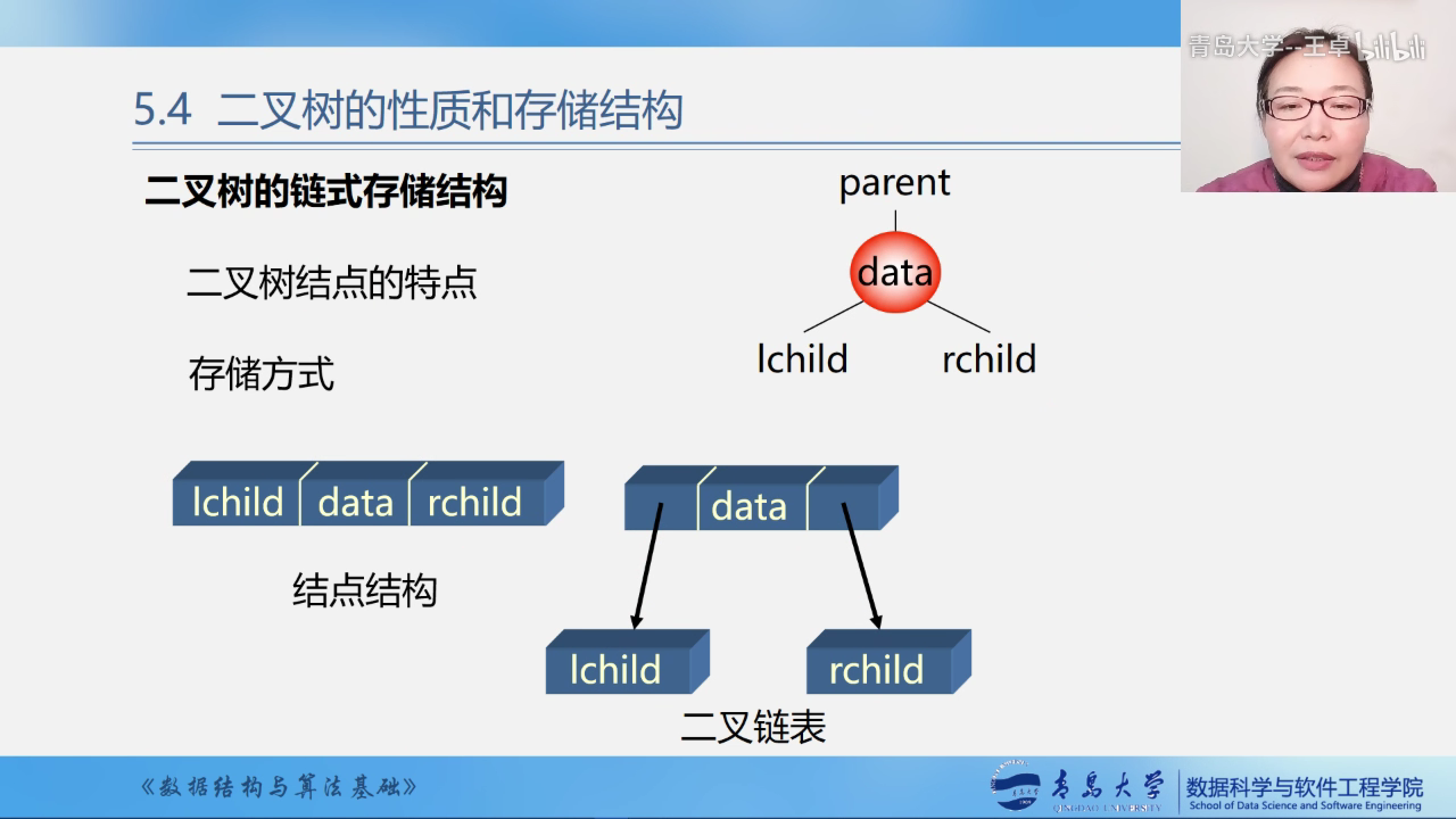
二叉树的链式存储结构
使用二叉链表储存二叉树,这样的存储结构可以动态扩展.
二叉链表示意图
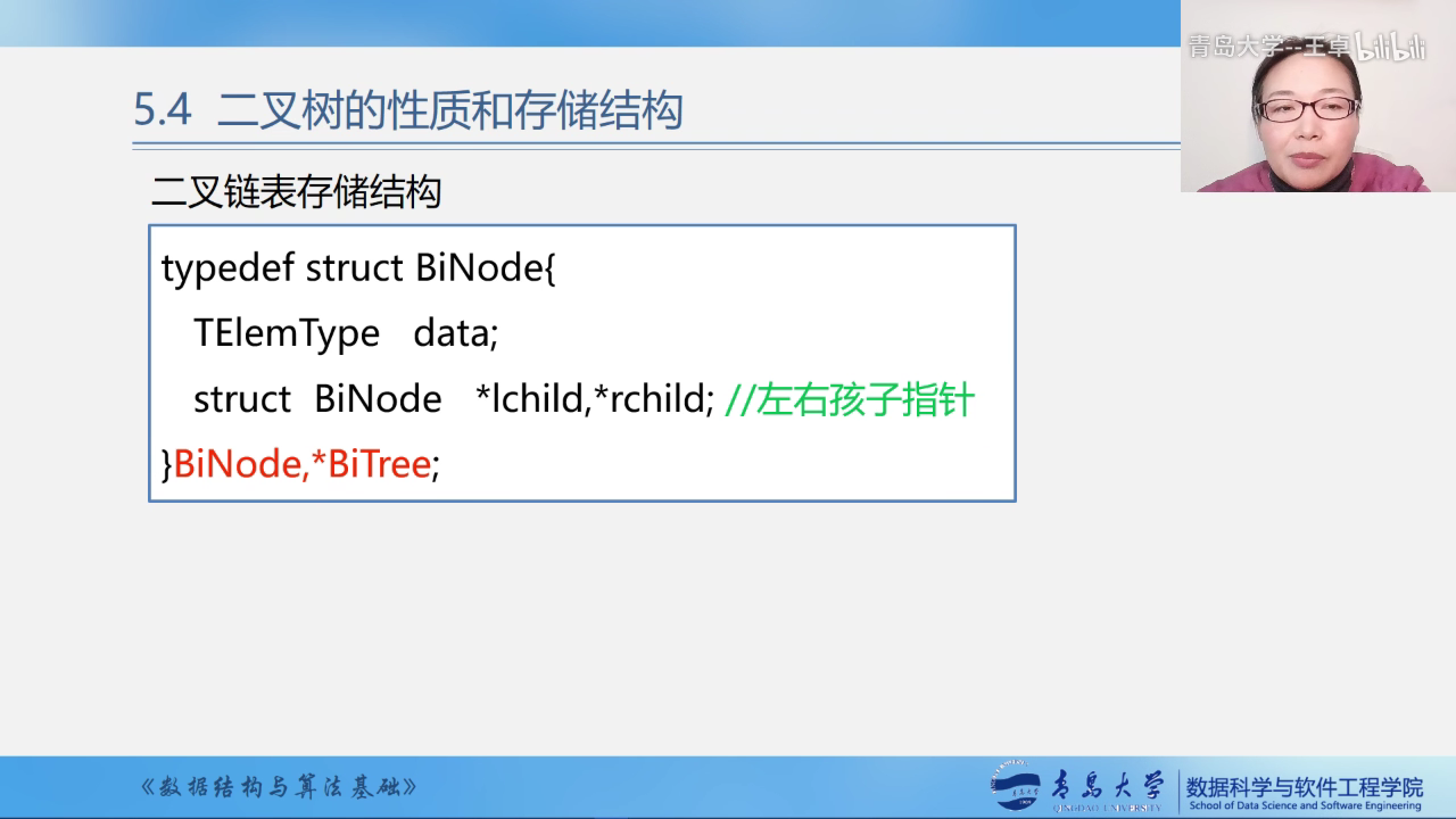
二叉链表的抽象数据结构
#include <iostream>
using namespace std;
typedef struct BiNode {
int data;//数据域
struct BiNode *lchild, *rchild; //左孩子指针和右孩子指针
} BiNode, *BiTree;
signed main () {
return 0;
}
二叉树链式存储示意图
两个指针域如果没有该方向没有孩子就设置为NULL,否则指向下一个结点,注意这里的二叉树的结点的定义是递归的定义的.
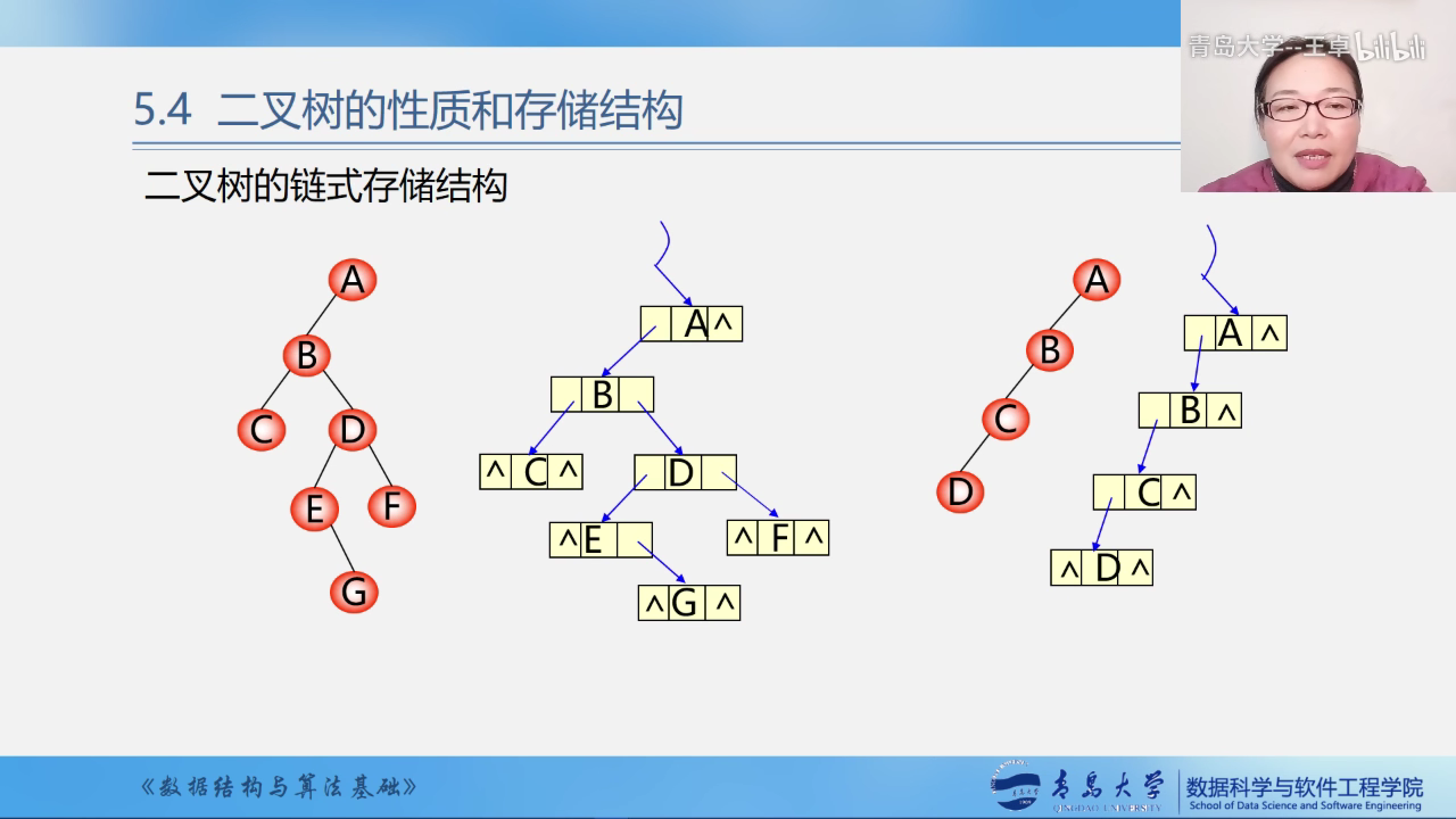
空指针域和结点的关系
可以从边上来看(蓝色的箭头),因为根结点是没有双亲的,所以只有n-1个结点有向上的蓝色箭头.因为n个结点有2n个指针域,所以由上面的规律可以看出有n-1个指针域不为空(都指向其孩子结点).所以2n-(n-1)为n+1所以有n+1个空指针域.

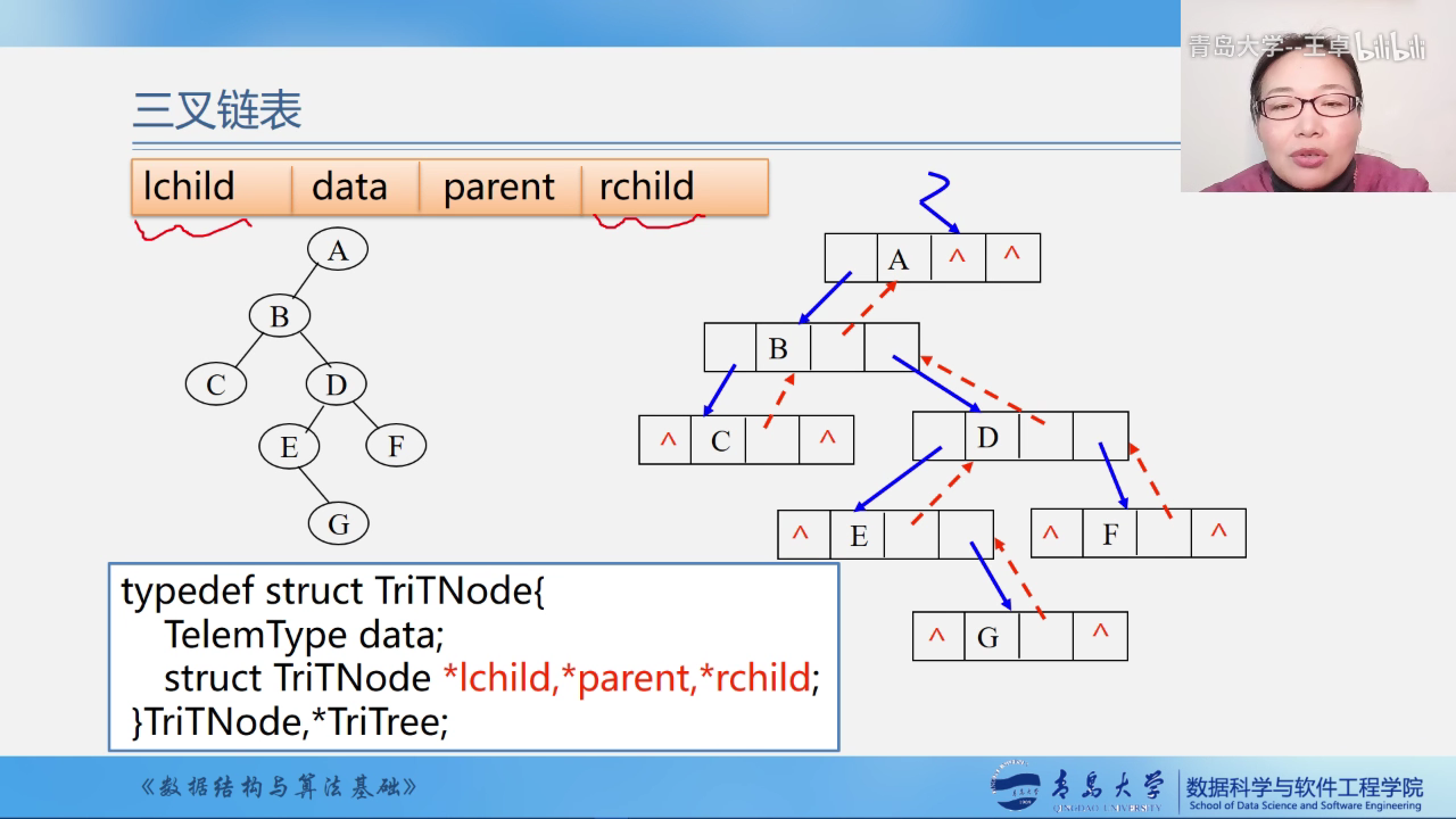
三叉链表
除了有指向左孩子和右孩子的指针还有一个指向双亲的指针,便于从当前结点找到双亲结点,以解决二叉链表无法找到其双亲结点的弊端.
但是总体来说还是二叉链表使用的较为频繁.
#include <iostream>
using namespace std;
typedef struct TriNode {
int data;
struct TriNode *lchild, *rchild, *parent; //左孩子指针,右孩子指针和双亲指针
} TriNode, *TirTree;
signed main () {
return 0;
}