最小生成树（普里姆算法）

试实现普里姆最小生成树算法。

函数接口定义：

void Prim(AMGraph G, char u);

其中 G 是基于邻接矩阵存储表示的无向图，u表示起点

裁判测试程序样例：

#include <iostream>
#define MVNum 10
#define MaxInt 32767 
using namespace std;

struct edge{
    char adjvex;
    int lowcost;
}closedge[MVNum];

typedef struct{ 
    char vexs[MVNum];   
    int arcs[MVNum][MVNum]; 
    int vexnum,arcnum;
}AMGraph;
int LocateVex(AMGraph G , char v);//实现细节隐藏
int Min(AMGraph G);//实现细节隐藏
int CreateUDN(AMGraph &G);//实现细节隐藏

void Prim(AMGraph G, char u);

int main(){
    AMGraph G;
    CreateUDN(G);
    char u;
    cin >> u;
    Prim(G , u);
    return 0;
}

/* 请在这里填写答案 */

输入样例：

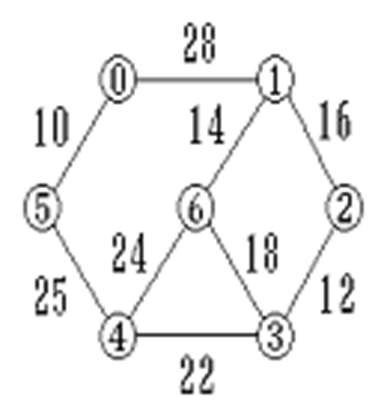
第1行输入结点数vexnum和边数arcnum。第2行输入vexnum个字符表示结点的值，接下来依次输入arcnum行，每行输入3个值，前两个字符表示结点，后一个数表示两个结点之间边的权值。最后一行输入一个字符表示最小生成树的起始结点。

7 9
0123456
0 1 28
0 5 10
1 2 16
1 6 14
2 3 12
3 6 18
3 4 22
4 5 25
4 6 24
0

输出样例：

按最小生成树的生成顺序输出每条边。

0->5
5->4
4->3
3->2
2->1
1->6

void Prim(AMGraph G, char u)
{
    int n=G.vexnum;
    int d[n],p[n];
    int index=0;
    int i,min=MaxInt,imin,count=0;
    for(i=0;i<n;i++)
    {
        if(G.vexs[i]==u){
            index=i;
        }
    }
    for(i=0;i<n;i++)
    {
        if(i==index)
        {
            d[i]=0;
            p[i]=index;
        }else
        {
            d[i]=G.arcs[index][i];
            p[i]=index;
        }
    }
    while(1)
    {
        if(count==n-1)
        {
            break;
        }

        for(i=0;i<n;i++)
        {
            if(d[i]!=0&&d[i]<min)
            {
                min=d[i];
                imin=i;
            }
        }
     count++;
        if(count<n-1){
            printf("%c->%c\n",G.vexs[p[imin]],G.vexs[imin]);
        }else
        {
            printf("%c->%c",G.vexs[p[imin]],G.vexs[imin]);
        }
        min=MaxInt;
        d[imin]=0;
        for(i=0;i<n;i++)
        {
            if(d[i]!=0&&G.arcs[i][imin]<min)
            {
                if(d[i]>G.arcs[i][imin])
                {
                    d[i]=G.arcs[i][imin];
                    p[i]=imin;
                }
            }
        }
    }
}