五、一个已排好序的数组是一个最小堆吗?

文心一言：

一个已排好序的数组不一定是一个最小堆。最小堆是一种特殊的二叉树，它满足以下性质：对于任意节点 x，其父节点 y 的值都小于等于 x 的值。而一个已排好序的数组只是一个有序数组，它满足任意的元素都是按从小到大的顺序排列的，但并不一定满足最小堆的性质。因此，一个已排好序的数组不一定是一个最小堆。

讯飞星火：

不一定。一个已排好序的数组可以是一个最小堆，也可以是一个最大堆或完全二叉树等其他类型的堆。最小堆是指在堆中，每个节点的值都小于等于其左右子节点的值，并且根节点是最小的。而最大堆则是指在堆中，每个节点的值都大于等于其左右子节点的值，并且根节点是最大的。完全二叉树是一种特殊的二叉树，它的每个节点最多有两个子节点，且左子节点的值小于右子节点的值。因此，一个已排好序的数组可以是最小堆、最大堆或完全二叉树等其他类型的堆。

华为盘古：

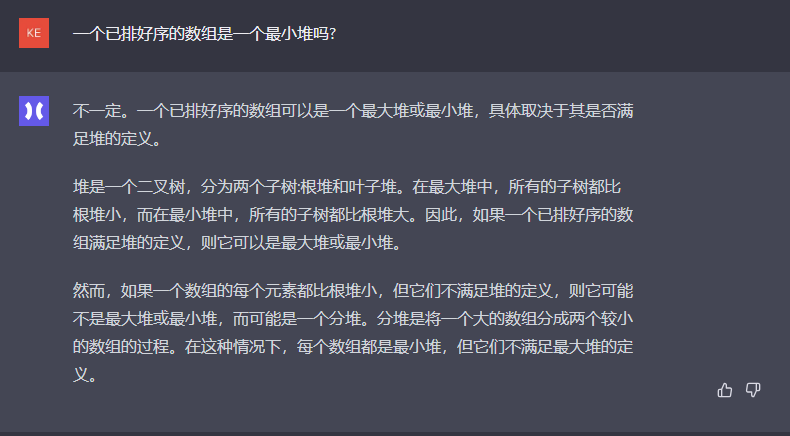
不一定。一个已排好序的数组可以是一个最大堆或最小堆，具体取决于其是否满足堆的定义。

堆是一个二叉树，分为两个子树:根堆和叶子堆。在最大堆中，所有的子树都比根堆小，而在最小堆中，所有的子树都比根堆大。因此，如果一个已排好序的数组满足堆的定义，则它可以是最大堆或最小堆。

然而，如果一个数组的每个元素都比根堆小，但它们不满足堆的定义，则它可能不是最大堆或最小堆，而可能是一个分堆。分堆是将一个大的数组分成两个较小的数组的过程。在这种情况下，每个数组都是最小堆，但它们不满足最大堆的定义。

360智脑：

不一定。最小堆是一种特殊的完全二叉树，其所有节点的值都大于或等于根节点的值，并且左子树和右子树的高度差不超过1。如果一个已排序的数组满足这些条件，那么它是一个最小堆。但是，如果数组中存在负数或者不是有序的，则它不一定是最小堆。

chatglm：

不一定。一个已排好序的数组不一定是一个最小堆。

chatgpt：

一个已经排好序的数组不一定是一个最小堆。在最小堆中，每个节点的值都小于或等于其子节点的值，但排好序的数组只要满足元素顺序的条件即可。

虽然排好序的数组可以满足最小堆的一部分性质，即父节点小于子节点的值，但它可能不满足另一个重要的性质，即堆结构的完整性。最小堆要求所有父节点的值都小于或等于其子节点的值，并且堆应该是完全二叉树结构。而排好序的数组可能违反这个完整性的要求，因此不能保证它一定是一个最小堆。

结论

一个已排好序的数组是一个最小堆，但是一个最小堆不一定是排好序的。