算法介绍
LRU
LRU 全称是 Least Recently Used,即最近最久未使用算法。
LRU 根据数据的历史访问记录来进行淘汰数据,其核心思想是“如果数据最近被访问过,那么将来被访问的几率也更高,它是页面置换算法的一种,也常用于缓存设计。
LFU
LFU 全称是 Least Frequently Used,根据频率来选择要淘汰的元素,即删除访问频率最低的元素,如果两个元素的访问频率相同,则淘汰访问频率最低的元素中最久没有被访问的元素。
数据结构
不管是 LRU 还是 LFU 算法,我们都需要使用到双向链表作为基础数据结构,由于 LRU 与 LFU 涉及的对双向链表的元素的操作比较复杂,还涉及对链表结点的其他操作,因此选择自己手写一个简单的双向链表,同时复习双向链表的实现(阿里一面就被问到了,半天没写对)。
这里根据 LRU 和 LFU 的需要,简单封装了删除结点、尾部插入结点、和判断双向链表是否为空三个函数,很大程度上简化了 LRU 和 LFU 的实现,降低了实现的出错概率。
struct Node {
Node() {
}
Node(int val, int key) :
val_(val), key_(key), next_(nullptr), pre_(nullptr) {
}
int val_;
int freq_;
Node *next_;
Node *pre_;
int key_;
};
struct List {
Node *vhead_; // 虚拟头结点
Node *vtail_; // 虚拟尾结点
int size_ = 0; // 链表中有效结点的数量
List() :
vhead_(new Node()), vtail_(new Node()) {
vhead_->next_ = vtail_;
vtail_->pre_ = vhead_;
vhead_->pre_ = nullptr;
vtail_->next_ = nullptr;
}
~List() {
delete vtail_;
delete vhead_;
vhead_ = nullptr;
vtail_ = nullptr;
}
void Insert(Node *node) {
// 双向链表的插入, node 表示待插入结点,插入作为双向链表的尾结点
node->pre_ = vtail_->pre_;
vtail_->pre_->next_ = node;
vtail_->pre_ = node;
node->next_ = vtail_;
++size_;
}
void Delete(Node *node) {
// node 指向待删除结点
node->next_->pre_ = node->pre_;
node->pre_->next_ = node->next_;
--size_;
}
bool Empty() {
return size_ <= 0;
}
};
LRU 实现
对于 LRU 的实现,我们需要借助两个数组结构哈希表和双向链表来组成一个新的数据结构。我们利用哈希表实现 $O(1)$ 时间复杂度的查找,获取元素的 val 以及在双向链表中的位置;利用双向链表实现 $O(1)$ 时间复杂度内的元素插入和删除。
- 删除元素时,要么通过哈希表获取了待删除元素在链表中的位置,要么是删除头结点;
- 删除元素后,需要在哈希表中也删除该元素,因此
Node需要有key_成员;
- 删除元素后,需要在哈希表中也删除该元素,因此
- 插入元素则都是插入到链表的末尾结点。
注意插入和删除时的结点数量变化,只有当结点数量小于 capacity 时插入结点需要递增 cnt_。
class LRUCache {
public:
LRUCache(int capacity) :
lst(new List()), cap_(capacity) {
}
int get(int key) {
if (hash.find(key) == hash.end()) {
return -1;
}
Node *node = hash[key];
lst->Delete(node);
lst->Insert(node);
return node->val_;
}
void put(int key, int value) {
if (hash.find(key) != hash.end()) {
// key 已经存在
Node *node = hash[key];
node->val_ = value;
node->key_ = key;
get(key);
return;
}
// key 不存在,需要插入
if (cnt_ == cap_) {
// 这里先插入或者先删除都能满足题义,我选择先插入,再删除(防止 capacity 为 0 的极限情况)
Node *node = new Node(value, key);
lst->Insert(node);
hash[key] = node;
// 删除头结点
Node *head = lst->vhead_->next_;
lst->Delete(head);
hash.erase(head->key_);
delete head;
head = nullptr;
} else {
// 直接插入即可
Node *node = new Node(value, key);
lst->Insert(node);
hash[key] = node;
// 记得修改数量
++cnt_;
}
}
private:
unordered_map<int, Node *> hash;
List *lst;
int cnt_ = 0;
int cap_;
};
LFU 实现
LFU 的实现比起 LRU 来说可要复杂太多了,要注意的地方也很多。LFU 需要用到两个哈希表,$N$ 个双向链表。
-
第一个哈希表是
key-node哈希表,如下图所示,key就是输入元素的key;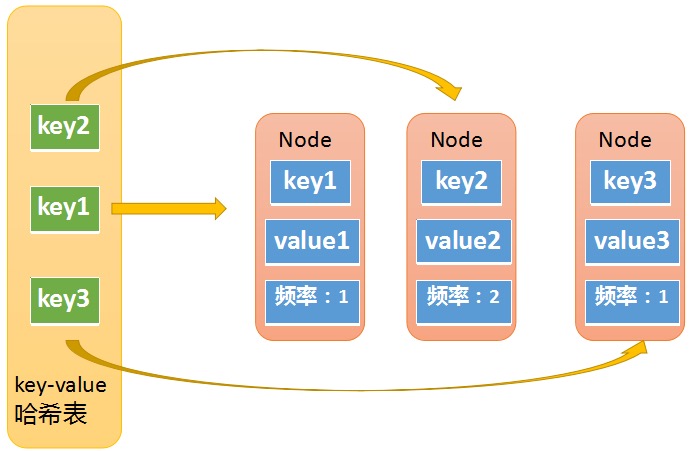
-
第二个哈希表则是
Freq-List哈希表,key是元素的使用频率,value是指向双向链表的指针,该双向链表与 LRU 中的双向链表形式类似。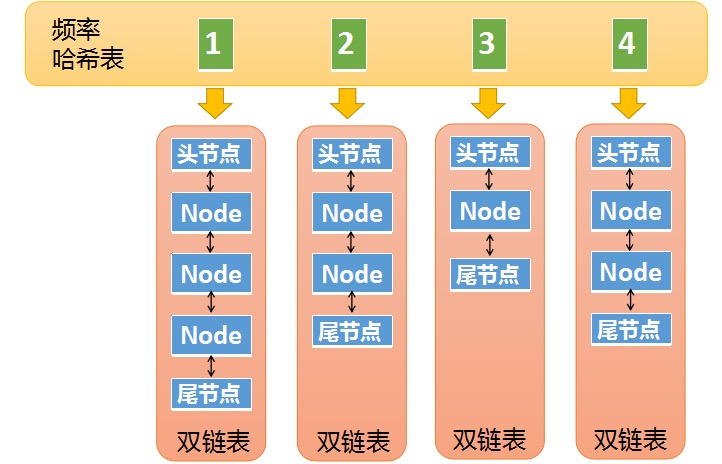
将两个哈希表看起来看一下完整的数据结构:
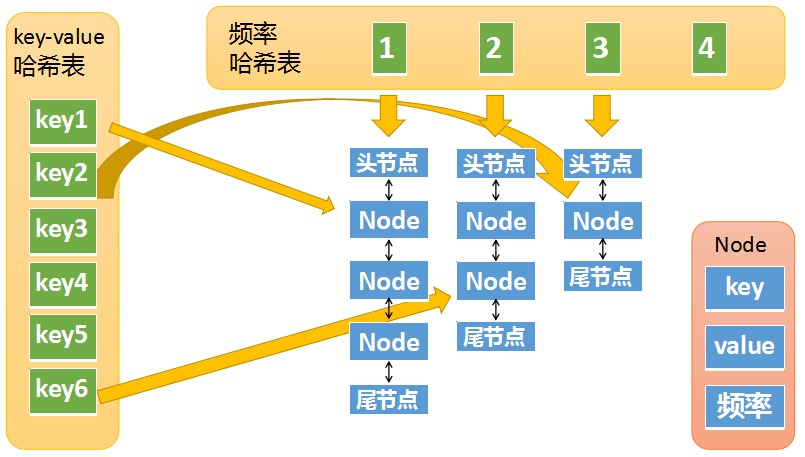
LFU 实现时,我们针对 get 操作和 put 操作分别讨论需要注意的地方。
get 操作相比 put 要简单一点,与 LRU 中的 get 操作类似,
- 区别在于要注意
get(key)时,与key对应的node的freq_需要递增,因此,还需要变更频率哈希表和它对应的链表;- 如果链表变成了空链表,需要从频率哈希表中移除空链表对应的频率。
put 操作则要复杂很多:
- 如果
key已经存在缓存中了,那么执行一次get(key)再更新一下node中的val_即可; - 如果
key不存在于缓存中,那么我们要分缓存已满和缓存未满两种情况来讨论:- 如果缓存已满,即
cnt_ == cap_,那么我们先执行删除结点,删除结点后,如果min_freq_对应的链表变成了空链表,那么就要delete该链表,并且从频率哈希表中移除该最小频率;然后插入该结点(结点频率为 1),并且更新min_freq_为 1; - 如果缓存未满,我们插入该结点(结点频率为 1),并且更新
min_freq_为 1。
- 如果缓存已满,即
class LFUCache {
public:
LFUCache(int capacity) :
cap_(capacity), min_freq_(0), cnt_(0) {
}
int get(int key) {
if (hash_.find(key) == hash_.end()) {
return -1;
}
Node *node = hash_[key];
int freq = node->freq_;
// 要更新频率,因此要从原先的频率链表上删除该结点
freqs_[freq]->Delete(node);
if (freqs_[freq]->Empty()) {
// 删除该链表,频率哈希表中移除该频率
delete freqs_[freq];
freqs_.erase(freq);
if (min_freq_ == freq) {
// 则需要更新最小频率
min_freq_ = freq + 1;
}
}
// 更新频率
++node->freq_;
freq = node->freq_;
if (freqs_.find(freq) == freqs_.end()) {
freqs_[freq] = new List();
}
freqs_[freq]->Insert(node);
return node->val_;
}
void put(int key, int value) {
// key 已经在缓存中了
if (hash_.find(key) != hash_.end()) {
get(key);
hash_[key]->val_ = value;
return;
}
/* key 不在缓存中 */
// 缓存已满
if (cnt_ == cap_) {
// 删除 min_freq_ 链表对应的头结点
List *lst = freqs_[min_freq_];
Node *to_del = lst->vhead_->next_;
lst->Delete(to_del);
hash_.erase(to_del->key_);
delete to_del;
to_del = nullptr;
// 如果 lst 变为空
if (lst->Empty()) {
delete lst;
lst = nullptr;
freqs_.erase(min_freq_);
}
// 现在执行插入
Node *node = new Node(value, key);
node->freq_ = 1;
min_freq_ = 1;
if (freqs_.find(node->freq_) == freqs_.end()) {
freqs_[node->freq_] = new List();
}
freqs_[node->freq_]->Insert(node);
hash_[key] = node;
} else {
// 现在执行插入
Node *node = new Node(value, key);
node->freq_ = 1;
min_freq_ = 1;
if (freqs_.find(node->freq_) == freqs_.end()) {
freqs_[node->freq_] = new List();
}
freqs_[node->freq_]->Insert(node);
hash_[key] = node;
++cnt_;
}
}
private:
unordered_map<int, Node *> hash_;
unordered_map<int, List *> freqs_;
int min_freq_;
int cnt_;
int cap_;
};
这里还要注意的是,类中 int 成员变量,如果没有在构造函数中显式执行初始化,其默认值很可能不是0。