首页 > 编程语言 >算法

算法

时间：2023-05-17 20:27:26浏览次数：40  
标签：arr temp int ++ 算法 && dp

算法

1 排序

1.1 直接插入排序

代码：

void insertSort(int arr[], int n) {
    int temp, j;
    for (int i = 1; i < n; i++) {
        temp = arr[i];
        
        j = i - 1;
        while (j >= 0 && temp < arr[j]) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = temp;
    }
}

1.2 简单选择排序

代码：

void selectSort(int arr[], int n) {
    int k, temp;  // 最小值在数组中下标
    for (int i = 0; i < n; i++) {
        k = i;
        for (int j = i + 1; j < n; j++)
            if (arr[k] > arr[j])
                k = j;
        temp = arr[i];
        arr[i] = arr[k];
        arr[k] = temp;
    }
}

1.3 冒泡排序

步骤：

  1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
  2. 对每一对相邻元素做同样的工作，执行完毕后，找到第一个最大值。
  3. 重复以上的步骤，每次比较次数-1，直到不需要比较

代码：

void bubleSort(int arr[], int n) {
    int flag, temp;
    for (int i = n - 1; i >= 1; i--) {
        flag = 0;
        for (int j = 1; j <= i; i++) {
            if (arr[j - 1] > arr[j]) {
                temp = arr[j];
                arr[j] = arr[j - 1];
                arr[j - 1] = temp;
                
                flag = 1;
            }
        }
        if (flag == 0) return;
    }
}

1.4 希尔排序

void shellSort(int arr[], int n) {
    int temp;
    for (int gap = n / 2; gap > 0; gap /= 2) {
        for (int i = gap; i < n; i++) {
            temp = arr[i];
            int j;
            for (j = i; j >= gap && arr[j - gap] > temp; j -= gap)
                arr[j] = arr[j - gap];
            arr[j] = temp;
        }
    }
}

1.5 快速排序

void quickSort(int arr[], int low, int high) {
    int temp;
    int i = low, j = high;
    if (low < high) {
        temp = arr[low];
        while (i < j) {
            while (j > i && arr[i] >= temp) j--;
            if (i < j) {
                arr[i] = arr[j];
                i++;
            }
            while (i < j && arr[i] < temp) i++;
            if (i < j) {
                arr[i] = arr[j];
                j--;
            }
        }
        arr[i] = temp;
        quickSort(arr, low, i - 1);
        quickSort(arr, i + 1, high);
    }
}

2 搜索

2.1 深度优先搜索（DFS）

2.1.1 回溯算法模板

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表);  // 递归
        回溯，撤销处理结果
    }
}

2.1.2 走迷宫（DFS）

题目描述：一天Extense在森林里探险的时候不小心走入了一个迷宫，迷宫可以看成是由n*n的格点组成，每个格点只有2种状态，.和#，前者表示可以通行后者表示不能通行。同时当Extense处在某个格点时，他只能移动到东南西北（或者说上下左右）四个方向之一的相邻格点上，Extense想要从点A走到点B,问在不走出迷宫的情况下能不能到。如果起点或者终点有一个不能通行（为#），则看成无法办到。

输入格式：第1行是一个正整数n(1<=n<=100),表示迷宫的规模是n*n的。接下来是一个n*n的矩阵，矩阵中的元素为 . 或者 # 。再接下来一行是4个整数ha,la,hb,lb,描述A处在第ha行，第la列，B处在第hb行，第lb列。注意到ha,la,hb,lb全部是从0开始计数的。

输出格式：能办到则输出“YES”,否则输出“NO”。

样例输入：

3
. # #
. # #
. . .
0 0 2 2

样例输出：

YES

代码：

#include <bits/stdc++.h> 
using namespace std;

char mp[100][100];  // 存储迷宫地区
bool vis[100][100] = {false};  // 记录是否走过，初始为false，走过记为true
int dir[4][2] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};  // 方向数组 
int n, sx, sy, ex, ey; // 地图尺寸，起点、终点坐标 
bool f = false;

// 判断坐标在不在地图范围内
bool in(int x, int y) {
	return x >= 0 && x < n && y >= 0 && y < n;
} 

// 走迷宫dfs递归函数
void dfs(int x, int y) {
	// 若到达终点，退出 
	if (x == ex && y == ey) {
		f = true;
		return;
	}
	for (int i = 0; i < 4; i++) {
        int tx = x + dir[i][0];
        int ty = y + dir[i][1];
    	// 条件为：在地图内，路未走过，路可以走
		// 必须先判断在不在地图内，不然vis[tx][ty]可能会发生数组越界
		if (in(tx, ty) && mp[tx][ty] != '#' && !vis[tx][ty]) {
			vis[x][y] = true;
			dfs(tx, ty);
			vis[x][y] = false;
		}
	}
}

int main()
{
	// 输入地图尺寸 
	cin >> n;
	
	// 输入迷宫地图 
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			cin >> mp[i][j];
		}
	}
	
	// 输入起点、终点坐标
	cin >> sx >> sy >> ex >> ey;
	
	// 若起点或终点为 # ，则输出no
	if (mp[sx][sy] == '#' || mp[ex][ey] == '#') {
		cout << "NO" << endl;
	} else {
		// 搜索，走迷宫
		dfs(sx, sy);
		// 判断是否到达
		if (f == true) {
			cout << "YES" << endl;
		} else {
			cout << "NO" << endl;
		}
	}
		
	return 0;
}

2.1.3 中国象棋（马）

题目描述：中国象棋博大精深，其中马的规则最为复杂，也是最难操控的一颗棋子。我们都知道象棋中马走“日“，比如在(2,4)位置的一个马，跳一步能到达的位置有(0,3)，(0,5)，(1,2)，(1,6)，(3,2)，(3,6)，(4,3)，(4,5)。

1

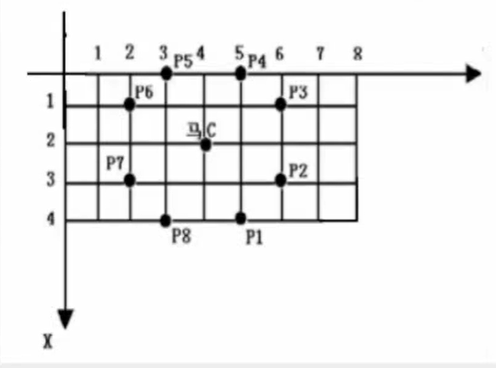
蒜头君正在和花椰妹下棋，蒜头君正在进行战略布局，他需要把在(x,y)位置的马跳到(x',y')位置以达到威慑的目的。
但是棋盘大小有限制，棋盘是一个10×9的网格，左上角坐标为(0,0)，右下角坐标为(9,8)，马不能走出棋盘，并且有些地方已经有了棋子，马也不能跳到有棋子的点。

蒜头君想知道，在不移动其他棋子的情况下，能否完成他的战略目标。

输入格式：

输入一共10行，每行一个长度为9的字符串。输入表示这个棋盘，我们用 '·' 表示空位置，用'#'表示该位置有棋子，用·S'表示初始的马的位置，用'T'表示马需要跳到的位置。输入保证一定只存在一个'S'和一个'T'。

输出格式：

如果在不移动其他棋子的情况下，马能从'S'跳到'T',那么输出一行"Yes”,否则输出一行"No”。

样例输入：

.#....#S#
..#.#.#..
..##.#..#
......##.
...T.....
...#.#...
...#.....
...###...
.........
.##......

样例输出：

Yes

代码：

#include <bits/stdc++.h>
using namespace std;

string s[10];  // 存储棋盘 
bool f = false;  // 是否抵达终点 
bool vis[10][9];  // 是否走过
int dir[8][2] = {{2, 1}, {1, 2}, {-1, 2}, {-2, 1}, {-2, -1}, {-1, -2}, {1, -2}, {2, -1}}; 

// 判断在棋盘内
bool in(int x, int y) {
	return x >=0 && x < 10 && y >= 0 && y < 9;
} 

void backtrack(int x, int y) {
	vis[x][y] = true;
	if (f == true) {
		return;
	}
	if (s[x][y] == 'T') {
		f = true;
		return;
	}
	for (int i = 0; i < 8; i++) {
		int tx = x + dir[i][0];
		int ty = y + dir[i][1];
		if (in(tx, ty) && s[tx][ty] != '#' && !vis[tx][ty]) {
			backtrack(tx, ty);
		}
	}
}


int main() {
	int sx, sy;  // 起点坐标 
	// 输入棋盘 
	for (int i = 0; i < 10; i++) {
		cin >> s[i];
	}
	// 初始化vis
	for (int i = 0; i < 10; i++) {
		for (int j = 0; j < 9; j++) {
			vis[i][j] = false;
		}
	} 
	// 找起点坐标
	for (int i = 0; i < 10; i++) {
		for (int j = 0; j < 9; j++) {
			if (s[i][j] == 'S') {
				sx = i;
				sy = j;
			}
		}
	} 
	backtrack(ex, ey);
	// 输出答案 
	if (f == true) {
		cout << "Yes" << endl;
	} else {
		cout << "No" << endl;
	}
		
	return 0;
}

2.1.4 从n个数中选k个数之和为sum

题目描述：

从n个数中选k个数之和为sum，共有ans种

样例输入：

5 3 9
1 2 3 4 5

样例输出：

2

代码：

#include <bits/stdc++.h>
using namespace std;

// 从n个数中选k个数之和为sum，共有ans种 
int n, k, sum, ans = 0; 
int a[40];

// i：第几个数，cnt：选了几个数，s：总和 
void dfs(int i, int cnt, int s) {
	if (i == n) {
		if (cnt == k && s == sum) {
			ans++;
		}
		return;
	}
	// 不选 
	dfs(i + 1, cnt, s);
	// 选 
	dfs(i + 1, cnt + 1, s + a[i]);  // 这里必须写cnt+1或者++cnt，不能写cnt++ 
}

int main() {
	cin >> n >> k >> sum;
	for (int i = 0; i < n; i++) {
		cin >> a[i];
	}
	dfs(0, 0, 0);
	cout << ans << endl;
	
	
	return 0;
}

2.2 广度优先搜索（BFS）

  • 一般是求最短路径问题

2.2.1 广度优先搜索模板

void bfs(起始点) {
    将起始点放入队列中；
    标记起点访问；
    while(如果队列不为空) {
        访问队列中队首元素x；
        删除队首元素；
        for (x 所有相邻点) {
            if (该点未被访问过且合法) {
                将该点加入队列末尾；
            }
        }
    }
    队列为空，广搜结束；
}

2.2.2 走迷宫（BFS）

#include <bits/stdc++.h> 
using namespace std;

char mp[100][100];  // 存储迷宫地区
bool vis[100][100] = {false};  // 记录是否走过，初始为false，走过记为true
int dir[4][2] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};  // 方向数组 
int n, sx, sy, ex, ey; // 地图尺寸，起点、终点坐标
bool f = false;

// 迷宫结点结构体 
struct Node {
    int x, y, step;
    Node(int x, int y, int step) {
        this->x = x;
        this->y = y;
        this->step = step;
    }
};

// 判断坐标在不在地图范围内
bool in(int x, int y) {
    return x >= 0 && x < n && y >= 0 && y < n; 
}

// 走迷宫bfs函数
void bfs() {
    queue<Node> q;
    // 起点加入队列 
    q.push(Node(sx, sy, 0));
    // 标记起点访问 
    vis[sx][sy] = true;

    while (!q.empty()) {
        // 访问队列中队首元素now
        Node now = q.front();
        // 删除队首元素
        q.pop();

        for (int i = 0; i < 4; i++) {
            int tx = now.x + dir[i][0];
            int ty = now.y + dir[i][1];
            // 该点未被访问过且合法
            if (in(tx, ty) && mp[tx][ty] != '#' && !vis[tx][ty]) {
                // 若到终点 
                if (tx == ex && ty == ey) {
                    f = true;
					return;
                } else {
                    // 将该点加入队列末尾
                    q.push(Node(tx, ty, now.step + 1));
                    vis[tx][ty] = true;
                }
            }
        }
    }
}

int main()
{
    // 输入地图尺寸 
    cin >> n;

    // 输入迷宫地图 
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            cin >> mp[i][j];
        }
    }

    // 输入起点、终点坐标
    cin >> sx >> sy >> ex >> ey;

    // 若起点或终点为 # ，则输出no
    if (mp[sx][sy] == '#' || mp[ex][ey] == '#') {
        cout << "NO" << endl;
    } else {
    	bfs(); 
        // 判断是否到达
        if (f == true) {
            cout << "YES" << endl;
        } else {
            cout << "NO" << endl;
        }
    }

    return 0;
}

3 动态规划

3.1 动态规划解题步骤

  1. 确定dp数组（dp table）以及下标的含义
  2. 确定递推公式
  3. dp数组如何初始化
  4. 确定遍历顺序
  5. 举例推导dp数组

3.2 01背包

题目描述：

有n件物品和一个最多能背重量为 w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

输入格式：

第一行输入n件商品，和背包容量b。

第二行开始，输入n行数据，第n行代表商品编号为n-2的商品信息，一行的第一个数据是商品重量w，第二个数据是商品价值v。

输出格式：

打印背包里最大的物品价值总和。

样例输入：

3 4
1 15
3 20
4 30

样例输出：

35

思路：

参考：代码随想录 - 01背包

  1. 确定dp数组（dp table）以及下标的含义：i：商品编号，j：背包容量，dp[i][j]：从编号 0 - i 的商品中任意取，再放进容量为 j 的背包中的最大价值。

  2. 确定递推公式：

    • 不放商品 i ：dp[i][j] = dp[i - 1][j]，第 i 个商品若不放，则0 - i 中任取与 0 - i - 1一样。

    • 放商品 i ：dp[i][j] = dp[i - 1][j - weight[i]] + value[i]，现确定放商品 i ，所以要加上value[i]，然后还要加上上一状态，上一状态要除去商品 i ，要在 0 - i - 1 中任取，背包容量也要减去商品 i 的重量，即dp[i - 1][j - weight[i]] + value[i]。

      所以递推公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

  3. dp数组如何初始化：

    • 初始化由递推公式确定，因为递推公式中有 i - 1 ，所以第一行需要初始化。然后，递推公式中有 j - weight[i] ，j 必须 >= weight[i] 时，才能放进背包，即 j - weight[i] >= 0 ，所以 j < weight[0] 的列需要初始化。
    • 如果背包容量 j < weight[0] 的话，无论是选取哪些物品，背包价值总和一定为0，所以 j < weight[0] 的列初始化为0 。
    • 第一行，dp[0][j]，即：i 为 0 ，存放编号0的物品的时候，各个容量的背包所能存放的最大价值。那么很明显当 j < weight[0]的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。当j >= weight[0]时，dp[0][j] 应该是value[0]，因为背包容量放足够放编号0物品。

  4. 确定遍历顺序：先遍历商品还是背包都可以。

  5. 举例推导dp数组

代码：

#include <bits/stdc++.h>
using namespace std;

const int MAX = 100;


int n, b;  // n：商品种类数量，b：背包容量 
int weight[MAX] = {0}, value[MAX] = {0};  // weight：商品重量，value：商品价值 
vector<vector<int> > dp(MAX, vector<int>(MAX, 0));  //dp数组，表示最大价值 

void test_01bag() {
	// 初始化
	for (int j = weight[0]; j <= b; j++) {
		dp[0][j] = value[0];
	} 
	
	// 遍历
	for (int i = 1; i < n; i++) {  // 遍历商品 
		for (int j = weight[0]; j <= b; j++) {  // 遍历背包容量
			if (j < weight[i]) {
				dp[i][j] = dp[i - 1][j];
			} else {
				dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
			}
		}
	}
}

int main() {
    // 数据输入 
	cin >> n >> b;
    
    for (int i = 0; i < n; i++) {
    	cin >> weight[i] >> value[i];
	}
	// 填dp数组
	test_01bag();
    
	// 打印答案
	cout << dp[n - 1][b] << endl; 

    return 0;
}

4 数论

4.1 最大公约数（gcd）和最小公倍数（lcm）

先使用辗转相除法求出gcd，再利用性质：\(lcm(a, b) = \frac{ab}{gcd(a, b)}\)，求出lcm

代码：

#include <iostream>
#include<algorithm>

using namespace std;

// 欧几里得算法，辗转相除法 
int gcd(int a, int b) {
	if (b == 0) {
		return a;
	}
	return gcd(b, a % b);
} 

int main() {
	int n, m;
	cin >> n >> m;
	
	int GCD1 = gcd(n, m);
	cout << GCD1 << endl;  // 最大公约数
	cout << n / GCD1 * m << endl;  // 最小公倍数，这里先除再乘，避免n×m可能过大
	
	// 使用c++的algorithm库函数__gcd()，返回值为最大公约数 
	int GCD2 = __gcd(n, m);
	cout << GCD2 << endl;  // 最大公约数
	cout << n / GCD2 * m << endl;  // 最小公倍数
	
	return 0;
}

4.2 质数筛选

  • 判断质数函数
// 判断质数
bool is_prime(int n)
{
    if (n <= 1) {
        return false;
    }
    if (n == 2) {
        return true;
    }
    for (int i = 2; i * i <= n; i++) {
        if (n % i == 0) {
            return false;
        }
    }
    return true;
}
  • 质数筛选（打印1~100质数）
#include <iostream>
using namespace std;

int main() {
    bool is_prime[105];
    // 先全部初始化为true
    for (int i = 2; i <= 100; i++) {
        is_prime[i] = true;
    }

    // 遍历2~10，其倍数记为false 
    for (int i = 2; i * i <= 100; i++) {
        if (is_prime[i] == true) {
            for (int j = i * i; j <= 100; j += i) {
                is_prime[j] = false;
            }
        }
    }
    // 打印结果 
    for (int i = 2; i <= 100; i++) {
        if (is_prime[i] == true) {
            cout << i << " ";
        }
    }

    return 0;
}

4.3 全排列

#include <bits/stdc++.h> 
using namespace std;


int a[3] = {1, 2, 3};
int n = 3;

void fullPermutation(int array[], int left, int right) {
    if (left == right) {
        for (int i = 0; i < n; i++) {
        	cout << array[i] << " ";
		}
        cout << endl;
    	
		return;
    }
    
    for (int i = left; i <= right; i++) {
        swap(array[i], array[left]);
        fullPermutation(array, left + 1, right);
        swap(array[i], array[left]);
    }
    
}


int main() {
	
	fullPermutation(a, 0, n - 1);
	
	
	return 0;
}

4.4 快速幂

题目描述：

求 \(a^b\%c\) 的值。其中 \(a,b,c\) 是整数，且 \(0 < a,c < 10^9, 0 < b < 10^{18}\) 。

代码：

#include <bits/stdc++.h>
using namespace std;


long long fast_power(long long a, long long b, long long c) {
	long long ans = 1;
	a %= c;
	while (b) {
		if (b & 1) {  // b % 2 == 1, 奇数 
			ans = (ans * a) % c;
		}
		a = (a * a) % c;
		b >>= 1;  // b /= 2 
	}
	return ans;
}

int main() {
    
    cout << fast_power(2, 5, 7) << endl;  // 2^5 % 7 = 4
	
    
    return 0;
}

4.5 质因数分解

题目链接： 蓝桥杯2022年第十三届省赛真题-质因数个数

题目描述：

给定正整数 n，请问有多少个质数是 n 的约数。

输入格式：

输入的第一行包含一个整数 n。

输出格式：

输出一个整数，表示 n 的质数约数个数。

样例输入：

396

样例输出：

3

提示：

396 有 2, 3, 11 三个质数约数。

对于 30% 的评测用例，1 ≤ n ≤ 10000。

对于 60% 的评测用例，1 ≤ n ≤ 109。

对于所有评测用例，1 ≤ n ≤ 1016。

思路：

对于任意一个正整数 ，可以将它分解成n个质因子的乘积

例如：

36=2*2*2*3*3

20=2*2*5

由此定理可以发现，对于正整数来说，它的任意一个因数都是它质因数的乘积，所有因数即是它质因数乘积的各种组合，由此可以快速的分解出一个数的所有因数

代码：

#include<iostream>
#include<cmath>

using namespace std;

typedef long long LL;

LL n;
LL cnt = 0;

int main() {
	cin >> n;
	
	if (n == 1) {
		cout << 0 << endl;
		return 0;
	}
	
	LL i; 
	for (i = 2; i <= sqrt(n) && n > 1; i++) {
		if (n % i == 0) cnt++;
		while (n % i == 0) {  // 去掉那些相同的质因子i 
			n /= i;
		}
	}
	
	if (i > 1) cnt++;  // 如果最后剩下的大于1，就加上余下的那个质因子 
	
	cout << cnt << endl;
	
	return 0; 
}

标签：arr,temp,int,++,算法,&&,dp
From： https://www.cnblogs.com/xiufanivan/p/17410027.html

相关文章

  • 无感FOC电机控制代码，算法采用滑膜观测器，SVPWM控制，启动采用Vf,全开源代码，很有参考价值
    无感FOC电机控制代码，算法采用滑膜观测器，SVPWM控制，启动采用Vf,全开源代码，很有参考价值。带原理图，SMO推导，附有相关的文档资料，matlab模型，电机控制资料。ID:858679491419183......
  • MATLAB仿真MIMO通信系统V-BALST结构ZF检测算 法与MMSE检测算法
    MATLAB仿真MIMO通信系统V-BALST结构ZF检测算法与MMSE检测算法商品形式：程序1、仿真V-BALST结构ZF检测算法性能，调制方式为QPSK2、仿真V-BALST结构MMSE检测算法性能，调制方式为QPSKID:4249643318184013......
  • 西门子Smart200 追剪算法程序送对应维纶屏监控程序 这算法是无级调速
    西门子Smart200追剪算法程序送对应维纶屏监控程序这算法是无级调速只是例程，一部PLC就能学习，需要使用理解后改变为自己需要的程序！只要一个PLC就可以运行，触摸屏直接用电脑模拟，如果接上步进伺服也可以直接运行ID:3110683180240276......
  • 神策杯 2018高校算法大师赛(个人、top2、top6)方案总结
    1竞赛背景神策数据推荐系统是基于神策分析平台的智能推荐系统。它针对客户需求和业务特点，并基于神策分析采集的用户行为数据使用机器学习算法来进行咨询、视频、商品等进行个性化推荐，为客户提供不同场景下的智能应用，如优化产品体验，提升点击率等核心的业务指标。神策推荐系统是一......
  • 山东算法赛网格事件智能分类topline
    赛题链接：http://data.sd.gov.cn/cmpt/cmptDetail.html?id=67baseline：https://aistudio.baidu.com/aistudio/projectdetail/3371314?contributionType=1分数：0.749+ 任务(1)赛题任务基于网格事件数据，对网格中的事件内容进行提取分析，对事件的类别进行划分，具体为根据提供的事件描述，......
  • 三相四桥臂逆变器MATLAB/Simulink仿真模型，接不平衡负载时的调制算法。
    三相四桥臂逆变器MATLAB/Simulink仿真模型，接不平衡负载时的调制算法。接非线性负载时的多PR控制器并联算法。提供仿真模型、参考文献ID:9835693184071748......
  • 常见的加密算法
    常见的加密算法有：AES：高级加密标准，对称加密算法，密钥长度128/192/256位，速度快，安全性高，目前最常用的对称加密算法之一。DES：数据加密标准，对称加密算法，密钥长度56位，速度快但密钥太短安全性较差，已被AES算法取代。3DES：增强版DES，使用3个不同的56位密钥，安全性比DES高但仍然不高，速度较慢......
  • 常见的非对称加密算法及主要特征
    常见的非对称加密算法有：RSA算法：最早提出的非对称加密算法，速度较慢但安全性高，密钥长度可达2048位。RSA使用乘法算术，加密和解密使用不同的密钥。RSA由三个数字(e,d,n)组成公钥和私钥。ECC算法：椭圆曲线加密算法，密钥长度短，速度更快，安全性同RSA。ECC基于椭圆曲线离散对数问题，密钥仅......
  • 还没期末考试，算法却说我的物理一定挂科
    By超神经场景描述：大学物理是理工科学生的基础必修课程，但也因为有一定的难度，令很多学生望而生畏。研究人员提出了用AI算法预测，哪些学生物理课有挂科风险，好让老师更好地进行教学指导和调整教育资源的分配。关键词：随机森林决策树大学物理预测不得不说，算法的预测能力越来越强，小到......
  • 代码随想录算法训练营第8天 | ● 344.反转字符串 ● 541. 反转字符串II ● 剑指Offer
     第四章 字符串part01  今日任务  ●  344.反转字符串●  541. 反转字符串II●  剑指Offer 05.替换空格●  151.翻转字符串里的单词●  剑指Offer58-II.左旋转字符串  详细布置   344.反转字符串  建议： 本题是字符串基础题目，就是考察......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99