最小费用最大流问题是经济学和管理学中的一类典型问题。在一个网络中每段路径都有“容量”和“费用”两个限制的条件下,此类问题的研究试图寻找出:流量从A到B,如何选择路径、分配经过路径的流量,可以在流量最大的前提下,达到所用的费用最小的要求。如n辆卡车要运送物品,从A地到B地。由于每条路段都有不同的路费要缴纳,每条路能容纳的车的数量有限制,最小费用最大流问题指如何分配卡车的出发路径可以达到费用最低,物品又能全部送到。
一、最小费用最大流问题
容量网络:图$D=(V,A,C) $
- \(V\):点集。其中 \(v_s\)为发点,只有发出的弧;\(v_t\)为收点,该点只有进入的弧;其余的点为中间点;
- \(A\): 弧集。对于每一条弧 \((v_i,v_j) \in A\)
- \(C\):容量集。每一条弧的容量$c(v_i,v_j)>=0 $(或简记为 \(c_{ij}\)),其中\(C=\{c_{ij}\}\)
- \(f:\) ${f_{ij}}={f(v_i,v_j)} $:弧 \((v_i,v_j)\)上的流量
可行流:
- 容量限制条件:$0\leq f_{ij} \leq _{ij} $
- 平衡条件:中间点:流出量 = 流入量 $$\sum_{j:\left(v_{i}, v_{j}\right) \in A} f_{i j}-\sum_{k:\left(v_{k}, v_{i}\right) \in A} f_{k i}=0$$
发点:
收点:
\[\sum_{k_{:} (v_{k}, v_{t}) \in A} f_{k t}=v \]式中:\(v\)称为这个可行流的流量,即发点的净输出量。
可行流的费用:设每条弧单位流量的费用记为\(b_{ij}\),可行流\(f\)费用为
\[b(f) = \sum \limits_{(v_i,v_j)} b_{ij} f_{ij} \]最小费用最大流问题就是在网络中求一个最大流\(f\),使流的总输送费用\(b(f)\)最小。
增流网络: 设\(f\)是网络 $D=(V,A,C,F,B) $的一个网络流,按照以下规则构建一个新的网络 \(D_{f}=(V,A^{'},C^{'},B^{'})\),该网络称为伴随\(f\)的增流网络,其中\(V\)为顶点集,\(A\)为弧集,\(C\)为容量集,\(F\)为流量集,\(B\)为费用集。
-
顶点:网络\(D_{f}\)与\(D\) 的顶点与网络的顶点相同;
-
弧与权:
- 在\(D\)中的弧\((v_i,v_j)\)若为零流弧,即\(f_{ij}=0\),则在\(D_{f}\)中构建一条同向的弧,\(c_{ij}^{'}=c_{ij}-f_{ij}\),\(b_{ij}^{'}=b_{ij}\)
- 在D中的弧\((v_i,v_j)\)若为饱和弧,即 \(f_{ij}=c_{ij}\),则在\(D_{f}\)中构建一条反向的弧\(c_{ij}^{'}=\_{ij}\), \(b_{ij}^{'}=-b_{ij}\)
- 在D中的弧\((v_i,v_j)\)若为非饱和弧,即\(f_{ij}<c_{ij}\),则在\(D_{f}\)中分别构建一条同向的弧和一条反向的弧,同向的弧 \(c_{ij}^{'}=c_{ij}-f_{ij}\), \(b_{ij}^{'}=b_{ij}\);反向的弧 \(c_{ij}^{'}=f_{ij}\), $b_{ij}^{'}=-b_{ij} $
-
负回路:在增流网络\(D_{f}\)中,所有的权(费用)之和小于零的回路称为负回路。
-
增流圈:在增流网络 \(D_{f}\)中的负回路对应网络\(D\)中的一个圈,在这个圈中,如果方向与这个负回路方向相同的所有弧都为不饱和弧,方向与负回路方向相反的所有弧都为非零流弧,则这个圈称为增流圈。
最大流问题的线性规划模型:
\[\begin{aligned} & \max v \\ & \text { s.t. }\left\{\begin{array}{l} \sum_{j:\left(v_i, v_j\right) \in A} f_{i j}-\sum_{j:\left(v_j, v_i\right) \in A} f_{j i}= \begin{cases}v, & i=s \\ -v, & i=t \\ 0, & i \neq s, t\end{cases} \\ 0 \leqslant f_{i j}, \forall\left(v_i, v_j\right) \in A \end{array}\right. \end{aligned} \]最小费用最大流问题的数学模型:
\[\begin{aligned} & \min \sum_{\left(v_i, v_j\right) \in A} b_{i j} f_{ij} \\ & \text { s.t. }\left\{\begin{array}{l} \sum_{j:\left(v_i, v_j\right) \in A} f_{i j}-\sum_{j:\left(v_j, v_i\right) \in A} f_{j i}= \begin{cases}v, & i=s \\ -v, & i=t \\ 0, & i \neq s, t\end{cases} \\ 0 \leqslant f_{i j}, \forall\left(v_i, v_j\right) \in A \\ f是最大可行流 \end{array}\right. \end{aligned} \]二、最小费用最大流的算法
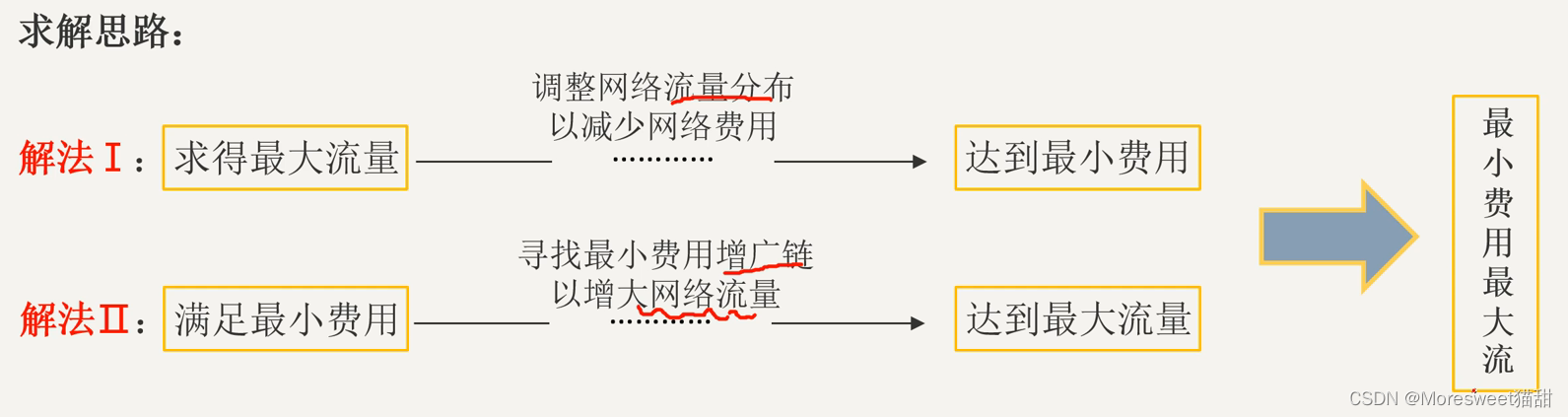
2.1 求得最大流量调整流量达到最小费用
利用最大流算法,将网络的流量调整到最大流
构建伴随网络流\(f\)的增流网络\(D_f\)
在增流网络\(D_f\) 中,查找关于费用的负回路,令\(\theta = \min \{c_{ij}^{'}\}\),(\(c_{ij}^{'}\)为负回路中各弧的容量),若不存在负回路,则说明当前网络流已经是最小费用流,结束算法。
针对负回路对应网络\(D\)中的圈,若该圈是增流圈,则把增流圈方向上与负回路方向一致的所有弧的流量加上\(\theta\),把增流圈方向上与负回路方向相反的所有弧的流量减去\(\theta\);若该圈不是增流圈,则转到步骤3重新寻找负回路。
2.2 寻找最小费用增广链达到最大流量
从网络\(D\)的零流\(f\)开始,构建伴随网络流\(f\)的增流网络\(D_f\)(此处\(D_f\) 中的权只需要费用\(c_{ij}^{'}\))
在增流网络\(D_{f}\)中用最短路径算法寻找从源到汇的最短路径,则该最短路径即对应网络\(D\)中的一条最小费用增广链;若找不到从源到汇的最短路,说明已经得到最大流,结束算法
在网络\(D\)中调整流量。前向弧上令\(\theta_{j}=c_{ij}-f_{ij}\),后向弧上令 \(\theta_{j}=f_{ij}\) ,调整量 $$ \theta =\min {\theta_j}$$
重复步前面骤,直到在增流网络\(D_{f}\) 中找不到从源到汇的最短路
三、最小费用最大流Pyhton程序
案例:给出下图网络的最小费用最大流(Minimum Cost Maximum Flow,MCMF)。

import numpy as np
import matplotlib.pyplot as plt # 导入 Matplotlib 工具包
import networkx as nx # 导入 NetworkX 工具包
# 3. 最小费用最大流问题(Minimum Cost Maximum Flow,MCMF)
# 创建有向图
G3 = nx.DiGraph() # 创建一个有向图 DiGraph
G3.add_edges_from([('s','v1',{'capacity': 13, 'weight': 7}),
('s','v2',{'capacity': 9, 'weight': 9}),
('v1','v3',{'capacity': 6, 'weight': 6}),
('v1','v4',{'capacity': 5, 'weight': 5}),
('v2','v1',{'capacity': 4, 'weight': 4}),
('v2','v3',{'capacity': 5, 'weight': 2}),
('v2','v5',{'capacity': 5, 'weight': 5}),
('v3','v4',{'capacity': 5, 'weight': 2}),
('v3','v5',{'capacity': 4, 'weight': 1}),
('v3','t',{'capacity': 4, 'weight': 4}),
('v4','t', {'capacity': 9, 'weight': 7}),
('v5','t',{'capacity': 9, 'weight': 5})]) # 添加边的属性 'capacity', 'weight'
# 求最小费用最大流
minCostFlow = nx.max_flow_min_cost(G3, 's', 't') # 求最小费用最大流
minCost = nx.cost_of_flow(G3, minCostFlow) # 求最小费用的值
maxFlow = sum(minCostFlow['s'][j] for j in minCostFlow['s'].keys()) # 求最大流量的值
# # 数据格式转换
edgeLabel1 = nx.get_edge_attributes(G3,'capacity') # 整理边的标签,用于绘图显示
edgeLabel2 = nx.get_edge_attributes(G3,'weight')
edgeLabel={}
for i in edgeLabel1.keys():
edgeLabel[i]=f'({edgeLabel1[i]:},{edgeLabel2[i]:})' # 边的(容量,成本)
edgeLists = []
for i in minCostFlow.keys():
for j in minCostFlow[i].keys():
edgeLabel[(i, j)] += ',f=' + str(minCostFlow[i][j]) # 将边的实际流量添加到 边的标签
if minCostFlow[i][j]>0:
edgeLists.append((i,j))
print("最小费用最大流的路径及流量: ", minCostFlow) # 输出最大流的途径和各路径上的流量
print("最小费用最大流的路径:", edgeLists) # 输出最小费用最大流的途径
print("最大流量: ", maxFlow) # 输出最大流量的值
print("最小费用: ", minCost) # 输出最小费用的值
最小费用最大流的路径及流量: {'s': {'v1': 11, 'v2': 9}, 'v1': {'v3': 6, 'v4': 5}, 'v2': {'v1': 0, 'v3': 4, 'v5': 5}, 'v3': {'v4': 2, 'v5': 4, 't': 4}, 'v4': {'t': 7}, 'v5': {'t': 9}, 't': {}}
最小费用最大流的路径: [('s', 'v1'), ('s', 'v2'), ('v1', 'v3'), ('v1', 'v4'), ('v2', 'v3'), ('v2', 'v5'), ('v3', 'v4'), ('v3', 'v5'), ('v3', 't'), ('v4', 't'), ('v5', 't')]
最大流量: 20
最小费用: 370