1、基础排序算法

接下类，我们学习另外一类非常基础的算法，即排序算法。
排序算法是计算机科学领域研究的非常深入的一类算法，排序这个动作本身也是非常重要的，
很多时候面对无需的数据，首先需要做的就是对他们进行排序。

排序算法——目的：让数据有序。
排序算法——种类：种类也非常多，适用于不同的情景。
排序算法——思想：蕴含着重要的计算机科学中的算法设计思想。

我们即将学习2个简单的排序算法：

• 1、选择排序法
• 2、插入排序法

通过对这2个基础的排序算法的学习，引申出更多东西，以打牢算法基础；
后续学习更加高级和更加复杂的算法时，可以有充分的准备。

特别是插入排序法，由于它的一些特殊性质，后续我们甚至在一些高级排序算法的学习中，甚至需要用到这种
类似插入排序这样的低级算法来进行一些优化。

2、选择排序法算法设计思想

我们接下来首先来看选择排序法。什么是选择排序法呢？它的思路本身很简单。
比如说，给我们一些待排序的元素，我们如何将这些本来是乱序的元素从小到大排列好呢？
非常简单，思路如下；

先在所有元素中将最小的元素拿出来
剩下的元素中，把最小的拿出来
剩下的元素中，把最小的拿出来
剩下的元素中，把最小的拿出来
……
只剩下一个元素，这个元素就是“剩下的元素中”最小的元素，将这最后一个元素拿出来

即：每次都选择还没处理的元素中最小的元素。
上述的思路就是选择排序法。

我们现在创建一个数组如下：

其中最小的元素是1：

拿出最小的元素1:

接着继续拿出最小的元素，分别拿出2、3、4：

直到所有“剩余的最小的元素”全部拿完，新的排序后数组出现：

我们上述的图片流程，我们的数组从6、3、2、1、5、4
到1、2、3、4、5、6的这个过程。

其实是使用了一个额外的数组空间，是从旧的数组6、3、2、1、5、4的基础上，新开辟了一个数组。
之后每次从旧的数组中找到剩下的元素中最小的元素，然后存储到新开辟的数组中……

这样一个过程，其实这样操作就占用了额外的空间，也是一种空间上的浪费。

接下来，我们要做的一个比较重要的事情是，我们的选择排序可否在原地完成？
这也是排序算法中非常重要的一个概念，即原地排序。

可以参考度娘的定义：原地排序

后续，我们会接触较多原地排序的算法，随着深入学习，我们会发现，有些算法可以用原地排序的方式实现；
但是对于另外一些排序算法，我们是无法原地排序实现的，必须借助额外的空间。

我们今天即将实现的选择排序就是一个可以原地排序的算法。

接下来，我们对选择排序进行图流程讲解。

我们直接实现原地排序的算法代码，
其实思路比较简单，我们每一轮找剩下的元素中最小的元素，我们只需要把我们找到的最小的元素直接放在数组开头的位置即可，即直接利用原来的数组空间即可。
举一个例子：
对于我们的数组的索引i，它初始的时候指着我们的数组索引为0的位置，表示我们现在想寻找排序之后的数组的第0个元素的位置应该是谁？

为了找到这个最小的元素，我们可以再增加一个索引j，这个索引j从索引为0的位置出发，扫描一遍所有的元素，找到其中最小的元素。
之后我们再使用一个minIndex索引，记录索引j找到的最小的元素所在的索引位置。

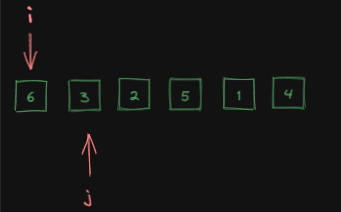
增加一个索引j，这个索引j从索引为0的位置出发，扫描一遍所有的元素:
j从0开始扫描：

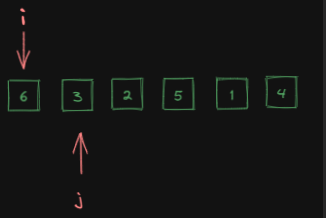
j扫描结束：

j找到的最小的元素所在的索引位置，记为minIndex：

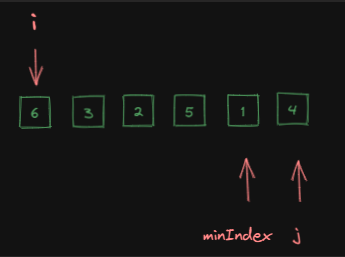
排序之后的数组，它所对应的元素，应该是此时minIndex指向的1这个元素，现在i这个位置指向的元素是6这个元素，
我们所要做的事情，只需要把1和6这两个元素交换位置，此时i=0这个位置的元素就已经是最小的那个元素了。
交换前：

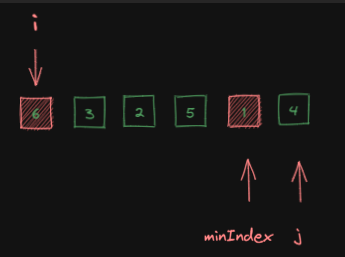
交换后：

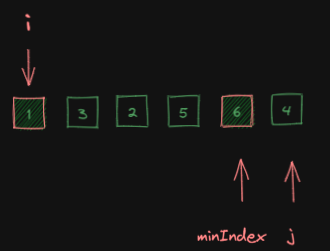
接下来，进一步，我们就可以做i=1的操作：

我们再做这一步的时候，我们就可以看到，每一步开始前，相当于arr[i……n)是未排序的（注意arr[i……n)是前闭后开）。
顺便提一句：这里的分析，用到了我们之前梳理过的循环不变量的知识。
循环不变量

从arr[1]到arr[n]都还没有排序，但是arr[0]已经排序好了。

arr[i……n)是未排序的（注意arr[i……n)是前闭后开）；
arr[i……n)中的最小值要放到arr[i]的位置；而原本arr[i]位置的元素，我们放到数组后面去，在后续的循环中继续处理。即min(arr[i]……arr[n]）与arr[i]做交换。

j从arr[i]出发：

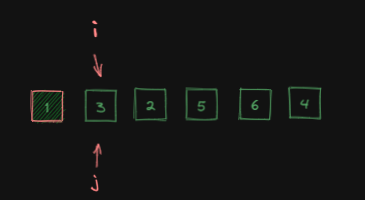
j扫描完整个数组：

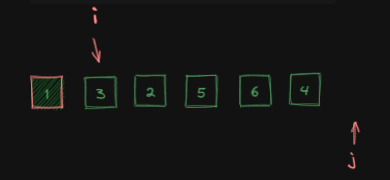
j扫描完整个数组后，找到最小元素的索引，记作minIndex:

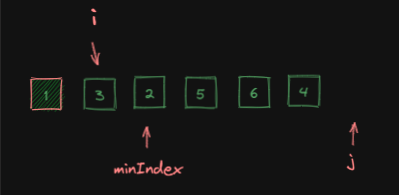
arr[i]与arr[minIndex]做交换：
交换前：

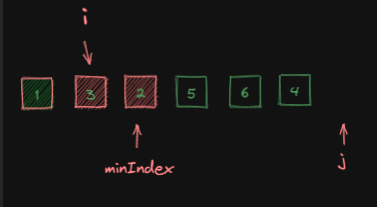
交换后：

此时arr[0]、arr[1]都已经排好序了。
下一轮循环开始前：

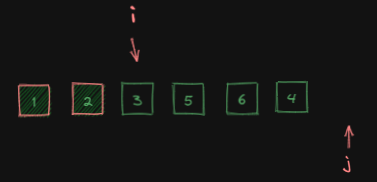
之后和前两轮循环一样，走完所有循环……
最后一轮循环过程如下：
j从arr[i]开始扫描：

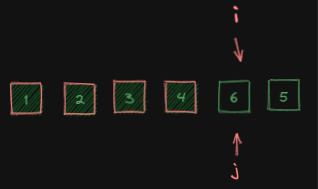
j扫描完整个数组：

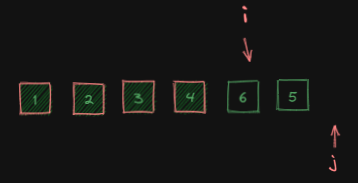
j扫描完整个数组后，找到最小元素的索引，记作minIndex:

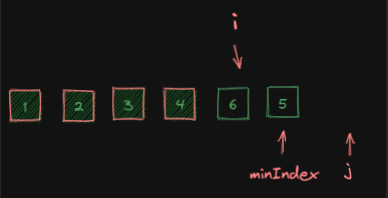
arr[i]与arr[minIndex]做交换：
交换前：

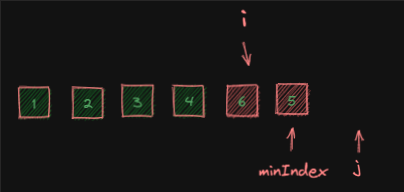
交换后：

至此，整个数组重新排序完成。
整个流程的关键是什么呢？

1、arr[i……n)未排序，arr[0……i)已排序；
2、arr[i……n]中的最小值要放到arr[i]的位置。

其中的1，1、arr[i……n)未排序，arr[0……i)已排序；(注，这个就是我们我们的选择排序法的循环不变量)
循环不变量

我们每一轮循环都在保持这个循环不变量，我们保持的方法就是2：
2、arr[i……n]中的最小值要放到arr[i]的位置。

这样，我们就原地完成了选择排序法。