标签：10 plt Python 数据 人工智能 print import data 我们

原文：Artificial Intelligence with Python

协议：CC BY-NC-SA 4.0

译者：飞龙

本文来自【ApacheCN 深度学习 译文集】，采用译后编辑（MTPE）流程来尽可能提升效率。

不要担心自己的形象，只关心如何实现目标。——《原则》，生活原则 2.3.c

6 集成学习的预测分析

在本章中，我们将学习集成学习以及如何将其用于预测分析。 在本章的最后，您将对这些主题有更好的理解：

• 决策树和决策树分类器
• 使用集成学习来学习模型
• 随机森林和极随机森林
• 预测的置信度估计
• 处理类别失衡
• 使用网格搜索找到最佳训练参数
• 计算相对特征重要性
• 使用极随机森林回归器预测交通

让我们从决策树开始。 首先，它们是什么？

什么是决策树？

决策树是将数据集划分为不同分支的方法。 然后遍历分支或分区以做出简单的决定。 决策树是由训练算法生成的，该算法确定了如何以最佳方式拆分数据。

决策过程从树顶部的根节点开始。 树中的每个节点都是决策规则。 算法基于输入数据和训练数据中目标标签之间的关系构造这些规则。 输入数据中的值用于估计输出值。

现在我们了解了决策树的基本概念，接下来要了解的概念是如何自动构建决策树。 我们需要可以根据数据构造最佳树的算法。 为了理解它，我们需要了解熵的概念。 在本文中，熵是指信息熵，而不是热力学熵。 信息熵基本上是不确定性的度量。 决策树的主要目标之一是减少从根节点到叶节点的不确定性。 当我们看到未知的数据点时，我们将完全不确定输出。 到叶子节点时，我们就可以确定输出了。 这意味着需要以减少每个级别的不确定性的方式构造决策树。 这意味着我们在沿着树前进时需要减少熵。

您可以在这里了解有关的更多信息。

建立决策树分类器

让我们看看如何使用 Python 中的决策树构建分类器。 创建一个新的 Python 文件并导入以下包：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import classification_report 
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier 

from utilities import visualize_classifier 

我们将使用提供给您的data_decision_trees.txt文件中的数据。 在此文件中，每一行都包含逗号分隔的值。 前两个值对应于输入数据，最后一个值对应于目标标签。 让我们从该文件加载数据：

# Load input data
input_file = 'data_decision_trees.txt'
data = np.loadtxt(input_file, delimiter=',')
X, y = data[:, :-1], data[:, -1] 

根据标签将输入数据分为两个单独的类：

# Separate input data into two classes based on labels
class_0 = np.array(X[y==0])
class_1 = np.array(X[y==1]) 

让我们使用散点图可视化输入数据：

# Visualize input data
plt.figure()
plt.scatter(class_0[:, 0], class_0[:, 1], s=75, facecolors='black',
        edgecolors='black', linewidth=1, marker='x')
plt.scatter(class_1[:, 0], class_1[:, 1], s=75, facecolors='white',
        edgecolors='black', linewidth=1, marker='o')
plt.title('Input data') 

我们需要将数据分为训练和测试数据集：

# Split data into training and testing datasets
X_train, X_test, y_train, y_test = train_test_split(
        X, y, test_size=0.25, random_state=5) 

基于训练数据集创建，构建和可视化决策树分类器。 random_state参数是指决策树分类算法初始化所需的随机数生成器使用的种子。 max_depth参数是指我们要构造的树的最大深度：

# Decision Trees classifier
params = {'random_state': 0, 'max_depth': 4}
classifier = DecisionTreeClassifier(**params)
classifier.fit(X_train, y_train)
visualize_classifier(classifier, X_train, y_train, 'Training dataset') 

计算测试数据集上分类器的输出并将其可视化：

y_test_pred = classifier.predict(X_test)
visualize_classifier(classifier, X_test, y_test, 'Test dataset') 

通过打印分类报告来评估分类器的表现：

# Evaluate classifier performance
class_names = ['Class-0', 'Class-1']
print("\n" + "#"*40)
print("\nClassifier performance on training dataset\n")
print(classification_report(y_train, classifier.predict(X_train), target_names=class_names))
print("#"*40 + "\n") 

print("#"*40)
print("\nClassifier performance on test dataset\n")
print(classification_report(y_test, y_test_pred, target_names=class_names))
print("#"*40 + "\n") 

plt.show() 

完整代码在decision_trees.py文件中给出。 如果运行代码，您将看到一些数字。 第一个屏幕截图是输入数据的可视化：

图 1：可视化输入数据

第二张屏幕截图显示了测试数据集上的分类器边界：

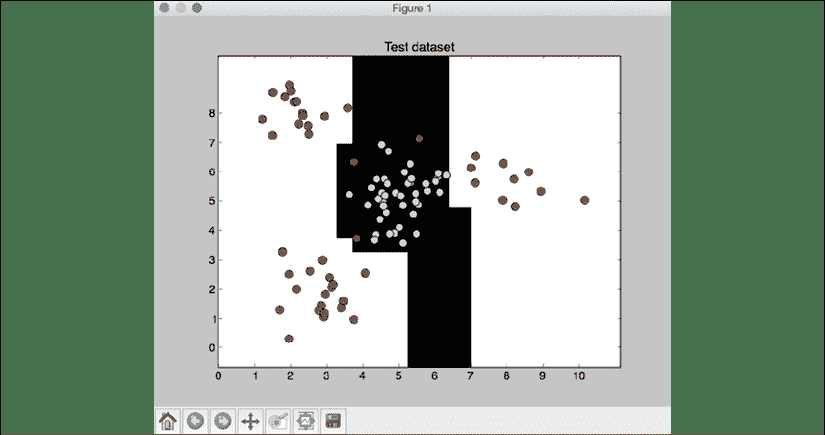
图 2：测试数据集的分类器边界

您还将看到以下输出：

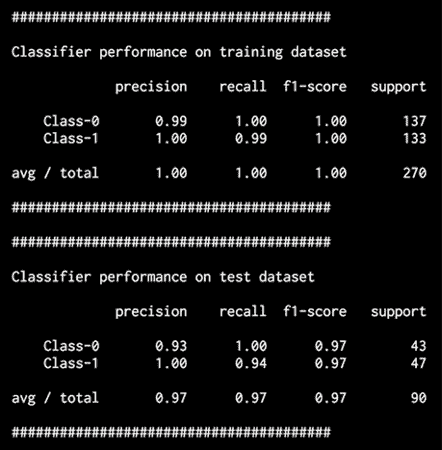
图 3：训练数据集上的分类器表现

分类器的表现以precision，recall和f1-scores为特征。 精度是指分类的准确率，召回率是指检索到的项目数占应检索的项目总数的百分比。 好的分类器将具有较高的精度和较高的查全率，但是通常在这两者之间需要权衡。 因此，我们有f1-score来表征。 F1 得分是精度和查全率的谐波平均值，使 F1 得分在精度和查全率之间取得了很好的平衡。

决策树是使用单个模型进行预测的示例。 通过组合和汇总多个模型的结果，有时可以创建更强大的模型和更好的预测。 一种方法是使用集成学习，这将在下一节中讨论。

什么是集成学习？

集成学习涉及建立多个模型，然后以使其产生比模型单独产生的结果更好的方式组合它们。 这些单独的模型可以是分类器，回归器或其他模型。

集成学习已广泛应用于多个领域，包括数据分类，预测建模和异常检测。

那么为什么要使用集成学习呢？ 为了获得理解，让我们使用一个真实的例子。 您想购买的新电视，但您不知道最新的型号是什么。 您的目标是使钱物有所值，但您对此主题的知识不足，无法做出明智的决定。 当您必须做出类似决定时，您可能会得到该领域内多位专家的意见。 这将帮助您做出最佳决定。 通常，您可以不依靠一种意见，而可以结合这些专家的个人决定来做出决定。 这样做可最大程度地减少错误或次优决策的可能性。

使用集成学习建立学习模型

选择模型时，常用的程序是选择训练数据集上误差最小的模型。 这种方法的问题在于，它并不总是有效。 该模型可能会出现偏差或过拟合训练数据。 即使使用交叉验证来训练模型，它也可能在未知数据上表现不佳。

集成学习模型之所以有效，是因为它们降低了选择不良模型的总体风险。 这使它能够以多种方式训练，然后在未知数据上表现良好。 使用集成学习构建模型时，各个模型需要表现出一定的多样性。 这使他们能够捕获数据中的各种细微差别。 因此整体模型变得更加准确。

通过为每个模型使用不同的训练参数来实现多样性。 这允许各个模型为训练数据生成不同的决策边界。 这意味着每个模型将使用不同的规则进行推断，这是验证结果的有效方法。 如果模型之间存在一致性，则可以增加预测的可信度。

集成学习的一种特殊类型是将决策树组合成一个集成。 这些模型通常被称为随机森林和极随机森林，我们将在接下来的章节中描述。

什么是随机森林和极随机森林？

随机森林是集成学习的实例，其中使用决策树构造单个模型。 然后，将这种决策树集合用于预测输出值。 我们使用训练数据的随机子集来构建每个决策树。

这将确保各种决策树之间的多样性。 在第一部分中，我们讨论了构建良好的集成学习模型时最重要的属性之一是确保各个模型之间存在多样性。

随机森林的优势之一是它们不会过拟合。 过拟合是机器学习中的常见问题。 非参数和非线性模型在学习目标函数时具有更大的灵活性，因此过拟合的可能性更大。 通过使用各种随机子集构建一组多样化的决策树，我们确保模型不会过拟合训练数据。 在树的构造过程中，将节点连续拆分，并选择最佳阈值以减小每个级别的熵。 此拆分未考虑输入数据集中的所有特征。 取而代之的是，它在考虑中的特征的随机子集中选择最佳分割。 添加此随机性往往会增加随机森林的偏差，但由于求平均值，方差会减小。 因此，我们最终得到了一个健壮的模型。

极随机森林将随机性提高到一个新水平。 除了采用特征的随机子集外，还随机选择阈值。 选择这些随机生成的阈值作为分割规则，这将进一步减小模型的方差。 因此，与使用随机森林获得的决策边界相比，使用极随机森林获得的决策边界趋于平滑。 极随机森林算法的某些实现还可以实现更好的并行化，并更好地扩展规模。

建立随机森林和极随机森林分类器

让我们看看如何可以基于随机森林和极其随机森林构建分类器。 构造两个分类器的方法非常相似，因此使用输入标志来指定需要构建哪个分类器。

创建一个新的 Python 文件并导入以下包：

import argparse 

import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier 
from sklearn.metrics import classification_report 

from utilities import visualize_classifier 

为 Python 定义一个参数解析器，以便我们可以将分类器类型作为输入参数。 依靠此参数，我们可以构造一个随机森林分类器或一个非常随机的森林分类器：

# Argument parser
def build_arg_parser():
    parser = argparse.ArgumentParser(description='Classify data using \
            Ensemble Learning techniques')
    parser.add_argument('--classifier-type', dest='classifier_type',
            required=True, choices=['rf', 'erf'], help="Type of classifier \
                    to use; can be either 'rf' or 'erf'")
    return parser 

定义main函数并解析输入参数：

if __name__=='__main__':
    # Parse the input arguments
    args = build_arg_parser().parse_args() 
    classifier_type = args.classifier_type 

我们将使用提供给您的data_random_forests.txt文件中的数据。 该文件中的每一行都包含逗号分隔的值。 前两个值对应于输入数据，最后一个值对应于目标标签。 在此数据集中，我们有三个不同的类。 让我们从该文件加载数据：

 # Load input data
    input_file = 'data_random_forests.txt'
    data = np.loadtxt(input_file, delimiter=',')
    X, y = data[:, :-1], data[:, -1] 

将输入数据分为三类：

 # Separate input data into three classes based on labels 
    class_0 = np.array(X[y==0])
    class_1 = np.array(X[y==1])
    class_2 = np.array(X[y==2]) 

让我们可视化输入数据：

 # Visualize input data
    plt.figure()
    plt.scatter(class_0[:, 0], class_0[:, 1], s=75, facecolors='white',
                    edgecolors='black', linewidth=1, marker='s')
    plt.scatter(class_1[:, 0], class_1[:, 1], s=75, facecolors='white',
                    edgecolors='black', linewidth=1, marker='o')
    plt.scatter(class_2[:, 0], class_2[:, 1], s=75, facecolors='white',
                    edgecolors='black', linewidth=1, marker='^')
    plt.title('Input data') 

将数据分为训练和测试数据集：

 # Split data into training and testing datasets
    X_train, X_test, y_train, y_test = train_test_split(
            X, y, test_size=0.25, random_state=5) 

定义构造分类器时要使用的参数。 n_estimators参数表示将要构建的树的数量。 max_depth参数指的是每棵树中的最大级别数。 random_state参数指的是初始化随机森林分类器算法所需的随机数生成器的种子值：

 # Ensemble Learning classifier
    params = {'n_estimators': 100, 'max_depth': 4, 'random_state': 0} 

根据输入参数，我们可以构造一个随机森林分类器或一个非常随机的森林分类器：

 if classifier_type == 'rf':
        classifier = RandomForestClassifier(**params)
    else:
        classifier = ExtraTreesClassifier(**params) 

训练和可视化分类器：

 classifier.fit(X_train, y_train)
    visualize_classifier(classifier, X_train, y_train, 'Training dataset') 

根据测试数据集计算输出并将其可视化：

 y_test_pred = classifier.predict(X_test)
    visualize_classifier(classifier, X_test, y_test, 'Test dataset') 

通过打印分类报告来评估分类器的表现：

 # Evaluate classifier performance
    class_names = ['Class-0', 'Class-1', 'Class-2']
    print("\n" + "#"*40)
    print("\nClassifier performance on training dataset\n")
    print(classification_report(y_train, classifier.predict(X_train), target_names=class_names))
    print("#"*40 + "\n")

    print("#"*40)
    print("\nClassifier performance on test dataset\n")
    print(classification_report(y_test, y_test_pred, target_names=class_names))
    print("#"*40 + "\n") 

完整的代码在random_forests.py文件中给出。 让我们使用输入参数中的rf标志，使用随机森林分类器运行代码。 运行以下命令：

$ python3 random_forests.py --classifier-type rf 

您会看到一些数字弹出。 第一个屏幕截图是输入数据：

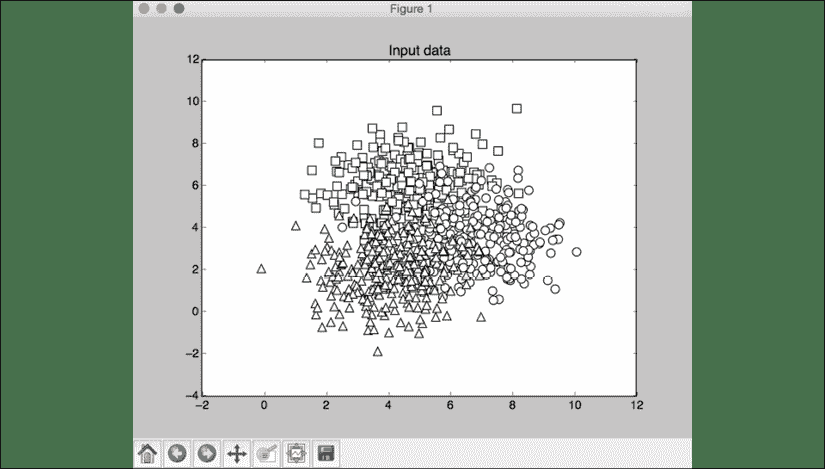
图 4：可视化输入数据

在前面的屏幕截图中，这三个类分别由正方形，圆形和三角形表示。 我们看到类之间有很多重叠，但是现在应该没问题。 第二张屏幕截图显示了分类器边界：

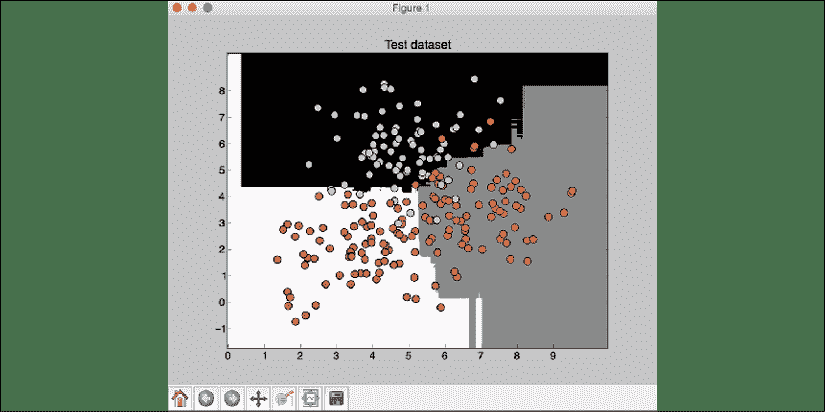
图 5：测试数据集上的分类器边界

现在，通过在输入参数中使用erf标志，使用极随机森林分类器运行代码。 运行以下命令：

$ python3 random_forests.py --classifier-type erf 

您会看到一些数字弹出。 我们已经知道输入数据的样子。 第二张屏幕截图显示了分类器边界：

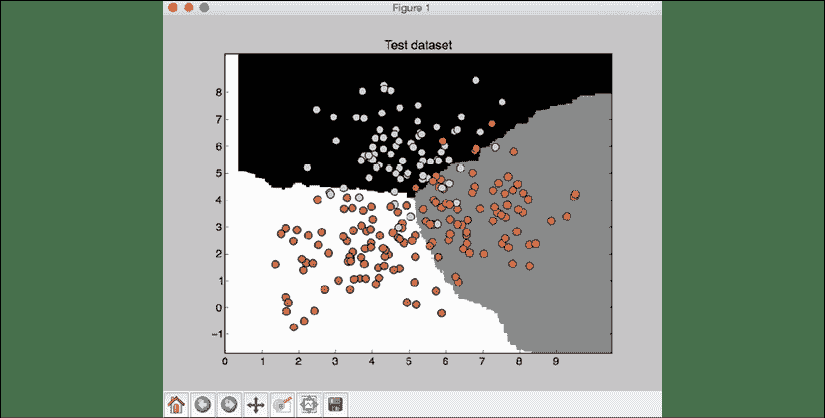
图 6：测试数据集上的分类器边界

如果将前面的屏幕截图与从随机森林分类器获得的边界进行比较，您会发现这些边界更平滑。 原因是，极随机的森林在训练的过程中拥有更多的自由来提出好的决策树，因此它们通常产生更好的边界。

估计预测的置信度

如果分析输出，将看到为每个数据点打印了概率。 这些概率用于测量每个类别的置信度值。 估计置信度值是机器学习中的重要任务。 在同一 Python 文件中，添加以下行以定义测试数据点的数组：

 # Compute confidence
    test_datapoints = np.array([[5, 5], [3, 6], [6, 4], [7, 2], [4, 4], [5, 2]]) 

分类器对象具有一种内置方法来计算置信度。 让我们对每个点进行分类并计算置信度值：

 print("\nConfidence measure:") 
    for datapoint in test_datapoints:
        probabilities = classifier.predict_proba([datapoint])[0]
        predicted_class = 'Class-' + str(np.argmax(probabilities))
        print('\nDatapoint:', datapoint)
        print('Predicted class:', predicted_class) 

根据分类器边界可视化测试数据点：

 # Visualize the datapoints
    visualize_classifier(classifier, test_datapoints, [0]*len(test_datapoints), 
            'Test datapoints') 

 plt.show() 

如果运行带有erf标志的代码，您将获得以下输出：

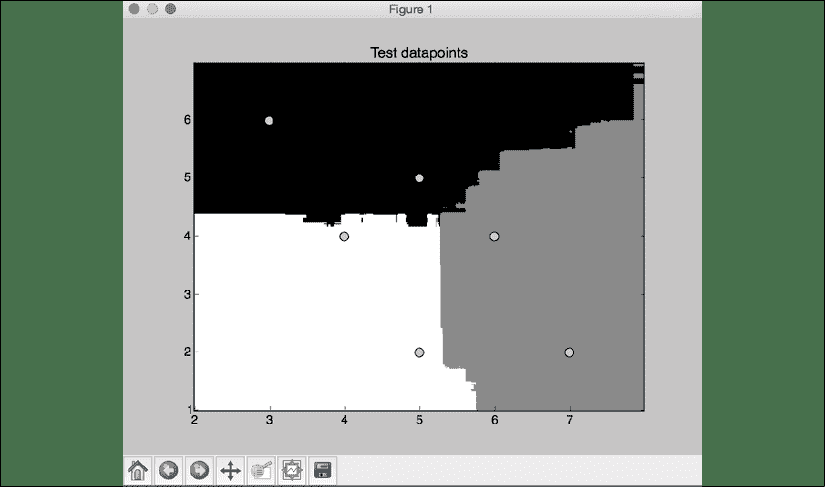
图 7：测试数据集上的分类器边界

没有erf标志，它将产生以下输出：

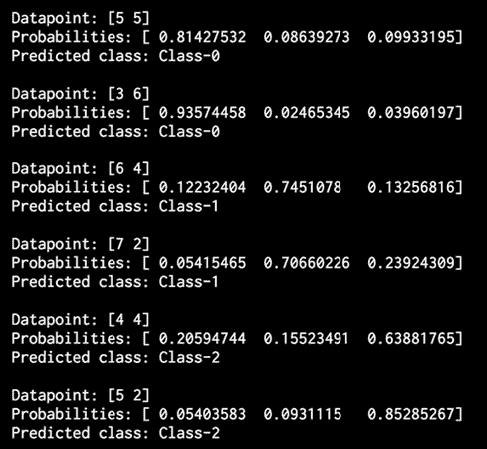
图 8：数据集概率输出

对于每个数据点，它计算该点属于我们的三类的概率。 我们选择最有信心的一个。 使用erf标志运行代码，您将获得以下输出：

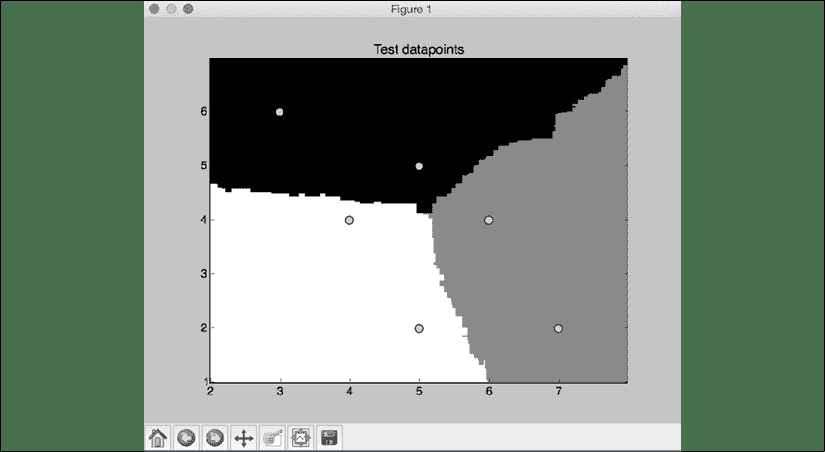
图 9：测试数据集上的分类器边界

如果没有erf标志，则应产生以下输出：

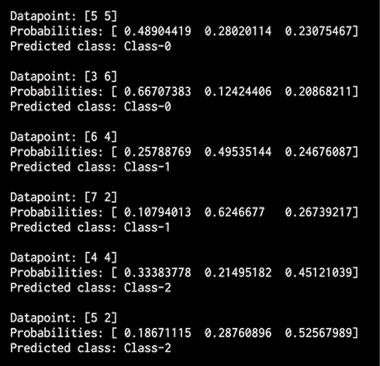
图 10：数据集概率输出

可以看出，输出由t与先前的结果组成。

处理类别失衡

分类器仅与用于训练的数据一样。 现实世界中面临的一个普遍问题是数据质量问题。 为了使分类器表现良好，每个分类器需要看到相等数量的点。 但是，当在现实世界中收集数据时，并不总是能够确保每个类都具有完全相同数量的数据点。 如果一个类别的数据点数是另一类别的 10 倍，则分类器倾向于偏向更多类别。 因此，我们需要确保考虑到这种不平衡算法。 让我们看看如何做到这一点。

创建一个新的 Python 文件并导入以下包：

import sys 

import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report 

from utilities import visualize_classifier 

我们将使用文件data_imbalance.txt中的数据进行分析。 让我们加载数据。

该文件中的每一行都包含逗号分隔的值。 前两个值对应于输入数据，最后一个值对应于目标标签。 我们在这个数据集中有两个类。 让我们从该文件加载数据：

# Load input data
input_file = 'data_imbalance.txt'
data = np.loadtxt(input_file, delimiter=',')
X, y = data[:, :-1], data[:, -1] 

将输入数据分为两类：

# Separate input data into two classes based on labels 
class_0 = np.array(X[y==0])
class_1 = np.array(X[y==1]) 

使用散点图可视化输入数据：

# Visualize input data
plt.figure()
plt.scatter(class_0[:, 0], class_0[:, 1], s=75, facecolors='black',
                edgecolors='black', linewidth=1, marker='x')
plt.scatter(class_1[:, 0], class_1[:, 1], s=75, facecolors='white',
                edgecolors='black', linewidth=1, marker='o')
plt.title('Input data') 

将数据分为训练和测试数据集：

# Split data into training and testing datasets
X_train, X_test, y_train, y_test = train_test_split.train_test_split(
        X, y, test_size=0.25, random_state=5) 

接下来，我们为极随机森林分类器定义参数。 请注意，有一个称为balance的输入参数可控制是否通过算法解决类不平衡问题。 如果是这样，则需要添加另一个名为class_weight的参数，该参数告诉分类器它应该权衡权重，以便与每个类中的数据点数量成正比：

# Extremely Random Forests classifier
params = {'n_estimators': 100, 'max_depth': 4, 'random_state': 0}
if len(sys.argv) > 1:
    if sys.argv[1] == 'balance':
        params = {'n_estimators': 100, 'max_depth': 4, 'random_state': 0, 'class_weight': 'balanced'}
    else:
        raise TypeError("Invalid input argument; should be 'balance'") 

使用训练数据构建，训练和可视化分类器：

classifier = ExtraTreesClassifier(**params)
classifier.fit(X_train, y_train)
visualize_classifier(classifier, X_train, y_train, 'Training dataset') 

预测测试数据集的输出并可视化输出：

y_test_pred = classifier.predict(X_test)
visualize_classifier(classifier, X_test, y_test, 'Test dataset') 

计算分类器的表现并打印分类报告：

# Evaluate classifier performance
class_names = ['Class-0', 'Class-1']
print("\n" + "#"*40)
print("\nClassifier performance on training dataset\n")
print(classification_report(y_train, classifier.predict(X_train), 
target_names=class_names))
print("#"*40 + "\n") 

print("#"*40)
print("\nClassifier performance on test dataset\n")
print(classification_report(y_test, y_test_pred, target_names=class_names))
print("#"*40 + "\n") 

plt.show() 

完整代码在文件class_imbalance.py中给出。 如果运行代码，您将看到以下图形。 第一个图表示输入数据：

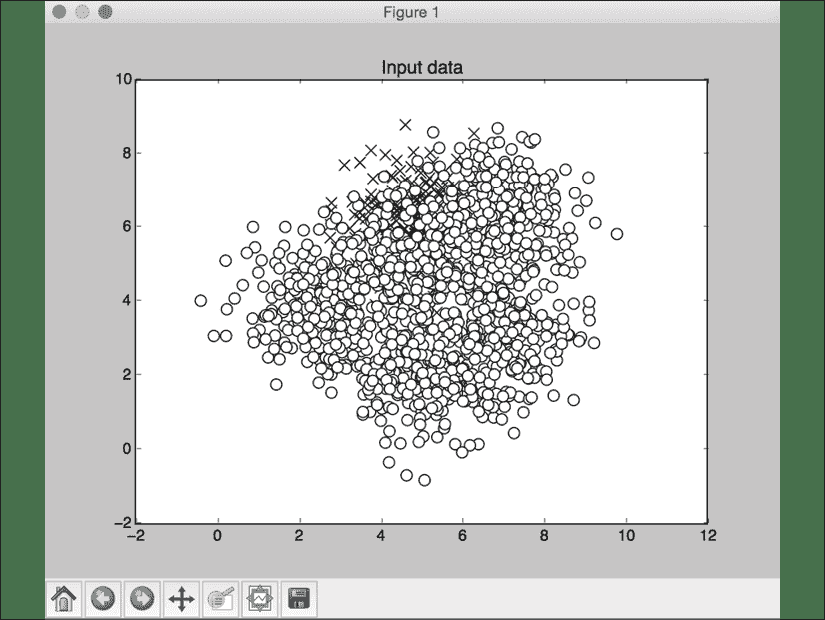
图 11：可视化输入数据

第二个图形显示了测试数据的分类器边界：

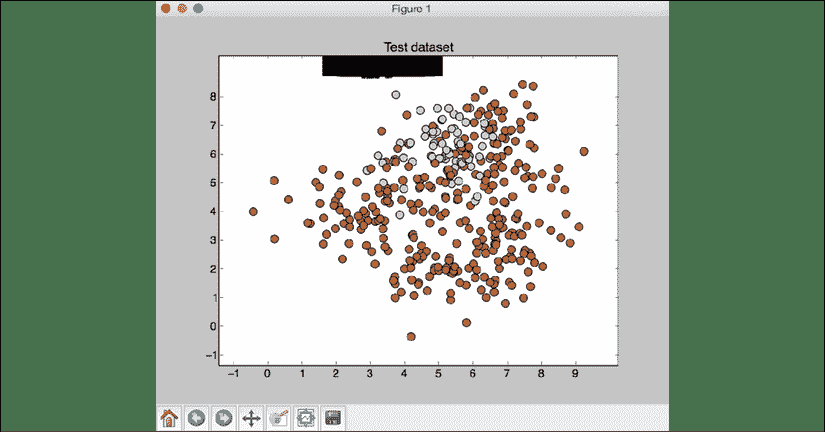
图 12：测试数据集上的分类器边界

前面的图形指示边界无法捕获两个类之间的实际边界。 顶部附近的黑色斑点代表边界。 最后，您应该看到以下输出：

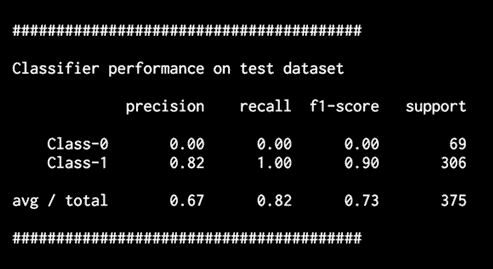
图 13：测试数据集上分类器的表现

您会看到一条警告，因为第一行的值为0，这在我们计算f1-score时会导致被零除的错误（ZeroDivisionError异常）。 使用ignore标志运行代码，以免看不到被零除警告：

$ python3 --W ignore class_imbalance.py 

现在，如果要解决类不平衡的问题，请使用balance标志运行它：

$ python3 class_imbalance.py balance 

分类器输出看起来像：

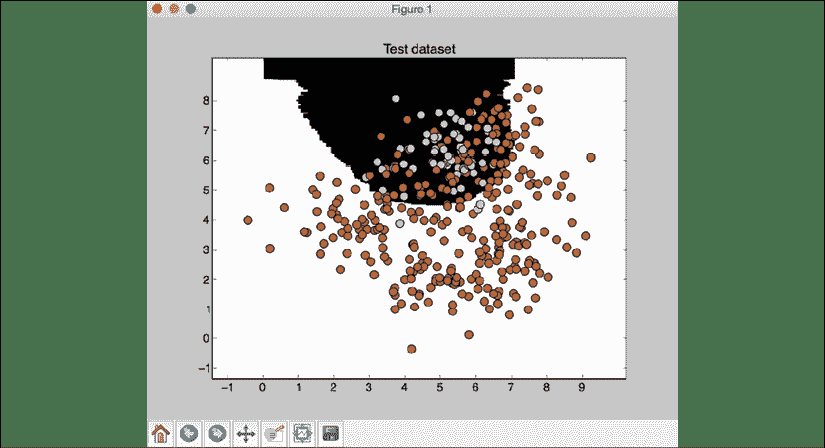
图 14：带有平衡的测试数据集的可视化

您应该看到以下输出：

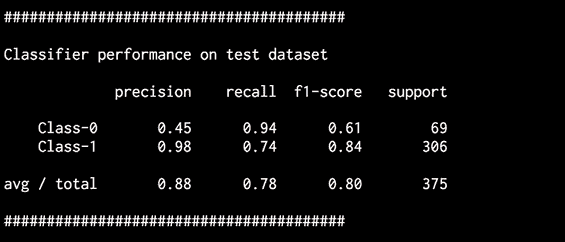
图 15：测试数据集上分类器的表现

通过考虑的类别不平衡，我们能够对的类别进行分类，从而使Class-0 中的数据点的整体精度不为零。

使用网格搜索找到最佳训练参数

在使用分类器时，并非总是可能知道要使用什么最佳参数。 通过手动检查所有可能的组合来使用暴力效率不高。 这是网格搜索变得有用的地方。 网格搜索使我们可以指定范围为的值，分类器将自动运行各种配置以找出参数的最佳组合。 让我们来看看如何做。

创建一个新的 Python 文件并导入以下包：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import classification_report
from sklearn import grid_search
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report 

from utilities import visualize_classifier 

我们将使用data_random_forests.txt中的可用数据进行分析：

# Load input data
input_file = 'data_random_forests.txt'
data = np.loadtxt(input_file, delimiter=',')
X, y = data[:, :-1], data[:, -1] 

将数据分为三类：

# Separate input data into three classes based on labels 
class_0 = np.array(X[y==0])
class_1 = np.array(X[y==1])
class_2 = np.array(X[y==2]) 

将数据分为训练和测试数据集：

# Split the data into training and testing datasets
X_train, X_test, y_train, y_test = cross_validation.train_test_split(
        X, y, test_size=0.25, random_state=5) 

指定参数的网格供分类器测试。 通常，一个参数保持恒定，而另一个参数变化。 然后进行反演以找出最佳组合。 在这种情况下，我们想找到n_estimators和max_depth的最佳值。 让我们指定参数网格：

# Define the parameter grid
parameter_grid = [{'n_estimators':[100], 'max_depth':[2,4,7,12,16]},
                 {'max_depth':[4],'n_estimators':[25,50,100,250]}] 

让我们定义分类器用来找到最佳参数组合的指标：

metrics = ['precision_weighted', 'recall_weighted'] 

对于每个指标，我们需要运行网格搜索，在其中训练分类器以获取参数组合：

for metric in metrics:
    print("\n##### Searching optimal parameters for", metric)

    classifier = grid_search.GridSearchCV(
            ExtraTreesClassifier(random_state=0),
            parameter_grid, cv=5, scoring=metric)
    classifier.fit(X_train, y_train) 

打印每个参数组合的分数：

 print("\nGrid scores for the parameter grid:")
    for params, avg_score, _ in classifier.grid_scores_:
        print(params, '-->', round(avg_score, 3))

    print("\nBest parameters:", classifier.best_params_) 

打印效果报告：

 y_pred = classifier.predict(X_test)
    print("\nPerformance report:\n")
    print(classification_report(y_test, y_pred)) 

完整代码在文件run_grid_search.py中给出。 如果运行代码，则将使用精度度量输出以下输出：

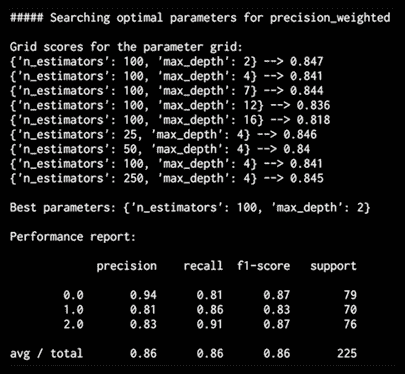
图 16：最佳参数搜索输出

基于网格搜索中的组合，它将打印出精度度量的最佳组合。 为了找到召回的最佳组合，可以检查以下输出：

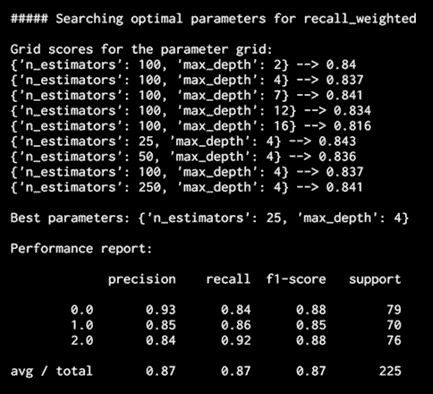
图 17：最佳参数搜索输出

这是用于召回的不同组合，使成为一体，因为精度和召回率是对和不同参数组合进行界定的不同指标。

计算特征相对重要性

在将与包含 N 维数据点的数据集一起使用时，必须理解，并非所有特征都同样重要。 有些比其他更具歧视性。 如果我们有此信息，则可以使用它来减少维数。 这对于降低复杂度和提高算法速度很有用。 有时，一些特征是完全多余的。 因此，可以轻松地将它们从数据集中删除。

我们将使用AdaBoost回归器计算特征重要性。 AdaBoost 是 Adaptive Boosting 的缩写，是一种经常与其他机器学习算法结合使用以提高其表现的算法。 在 AdaBoost 中，从分布中提取训练数据点以训练当前分类器。 该分布会进行迭代更新，以便后续的分类器可以专注于更困难的数据点。 困难的数据点是那些分类错误的数据点。 这是通过在每个步骤更新发行版来完成的。 这将使先前被错误分类的数据点更有可能出现在用于训练的下一个样本数据集中。

然后将这些分类器进行级联，并通过加权多数投票做出决定。

创建一个新的 Python 文件并导入以下包：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor 
from sklearn.ensemble import AdaBoostRegressor 
from sklearn import datasets
from sklearn.metrics import mean_squared_error, explained_variance_score 
from sklearn.model_selection import import train_test_split
from sklearn.utils import shuffle 

from utilities import visualize_feature_importances 

我们将使用 scikit-learn 中提供的内置房屋数据集：

# Load housing data
housing_data = datasets.load_boston() 

对数据进行混洗，以使不会偏向于分析：

# Shuffle the data
X, y = shuffle(housing_data.data, housing_data.target, random_state=7) 

将数据集分为训练和测试：

# Split data into training and testing datasets
X_train, X_test, y_train, y_test = train_test_split(
        X, y, test_size=0.2, random_state=7) 

使用决策树回归器作为单独模型来定义和训练AdaBoostregressor：

# AdaBoost Regressor model
regressor = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4),
        n_estimators=400, random_state=7)
regressor.fit(X_train, y_train) 

估计回归器的表现：

# Evaluate performance of AdaBoost regressor
y_pred = regressor.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
evs = explained_variance_score(y_test, y_pred )
print("\nADABOOST REGRESSOR")
print("Mean squared error =", round(mse, 2))
print("Explained variance score =", round(evs, 2)) 

此回归器具有一个内置方法，可以调用该方法来计算相对特征的重要性：

# Extract feature importances
feature_importances = regressor.feature_importances_
feature_names = housing_data.feature_names 

归一化相对特征重要性的值：

# Normalize the importance values 
feature_importances = 100.0 * (feature_importances / max(feature_importances)) 

对它们进行排序，以便可以进行绘制：

# Sort the values and flip them
index_sorted = np.flipud(np.argsort(feature_importances)) 

排列条形图在 x 轴上的刻度：

# Arrange the X ticks
pos = np.arange(index_sorted.shape[0]) + 0.5 

绘制条形图：

# Plot the bar graph
plt.figure()
plt.bar(pos, feature_importances[index_sorted], align='center')
plt.xticks(pos, feature_names[index_sorted])
plt.ylabel('Relative Importance')
plt.title('Feature importance using AdaBoost regressor')
plt.show() 

完整代码在文件feature_importance.py中给出。 如果运行代码，则应该看到以下输出：

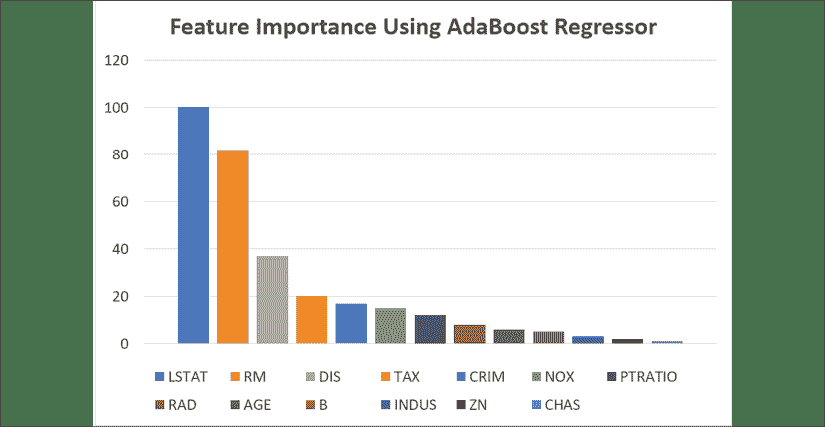
图 18：使用 Adaboost 回归器的特征重要性

根据这一分析，特征LSTAT是该数据集中最重要的特征。

使用极随机森林回归器预测流量

让我们将在上一节中学习的概念应用于一个实际问题。 我们将使用可用数据集。 该数据集包含对在洛杉矶道奇体育场（Lod Angeles Dodgers Stadium）进行的棒球比赛中道路上经过的车辆进行计数的数据。 为了使数据易于分析，我们需要对其进行预处理。 预处理后的数据在文件traffic_data.txt中。 在此文件中，每一行均包含逗号分隔的字符串。 让我们以第一行为例：

Tuesday,00:00,San Francisco,no,3 

参考上一行，其格式如下：

一周中的一天，一天中的时间，对手团队，指示棒球比赛当前正在进行的二进制值（是/否），经过的车辆数量。

我们的目标是通过使用给定的信息来预测车辆行驶的数量。 由于输出变量是连续值，因此我们需要构建一个可以预测输出的回归变量。 我们将使用极随机森林来构建此回归器。 让我们继续进行，看看如何做到这一点。

创建一个新的 Python 文件并导入以下包：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import classification_report, mean_absolute_error 
from sklearn import cross_validation, preprocessing
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.metrics import classification_report 

将数据加载到文件traffic_data.txt中：

# Load input data
input_file = 'traffic_data.txt'
data = []
with open(input_file, 'r') as f:
    for line in f.readlines():
        items = line[:-1].split(',')
        data.append(items) 

data = np.array(data) 

数据中的非数字特征需要进行编码。 不对数字特征进行编码也很重要。 每个需要编码的特征都需要有一个单独的标签编码器。 我们需要跟踪这些编码器，因为当我们要计算未知数据点的输出时将需要它们。 让我们创建那些标签编码器：

# Convert string data to numerical data
label_encoder = []
X_encoded = np.empty(data.shape)
for i, item in enumerate(data[0]):
    if item.isdigit():
        X_encoded[:, i] = data[:, i]
    else:
        label_encoder.append(preprocessing.LabelEncoder())
        X_encoded[:, i] = label_encoder[-1].fit_transform(data[:, i])
X = X_encoded[:, :-1].astype(int)
y = X_encoded[:, -1].astype(int) 

将数据分为训练和测试数据集：

# Split data into training and testing datasets
X_train, X_test, y_train, y_test = cross_validation.train_test_split(
        X, y, test_size=0.25, random_state=5) 

训练一个非常随机的森林回归器：

# Extremely Random Forests regressor
params = {'n_estimators': 100, 'max_depth': 4, 'random_state': 0}
regressor = ExtraTreesRegressor(**params)
regressor.fit(X_train, y_train) 

根据测试数据计算回归器的表现：

# Compute the regressor performance on test data
y_pred = regressor.predict(X_test)
print("Mean absolute error:", round(mean_absolute_error(y_test, y_pred), 2)) 

让我们看看如何计算未知数据点的输出。 标签编码器将用于将非数字特征转换为数值：

# Testing encoding on single data instance 
test_datapoint = ['Saturday', '10:20', 'Atlanta', 'no'] 
test_datapoint_encoded = [-1] * len(test_datapoint) 
count = 0
for i, item in enumerate(test_datapoint): 
    if item.isdigit():
        test_datapoint_encoded[i] = int(test_datapoint[i])
    else:
        test_datapoint_encoded[i] = int(label_encoder[count].transform(test_datapoint[i]))
        count = count + 1 

data = np.array(data)
test_datapoint_encoded = np.array(test_datapoint_encoded) 

预测输出：

# Predict the output for the test datapoint
print("Predicted traffic:", int(regressor.predict([test_datapoint_encoded])[0])) 

完整代码在文件traffic_prediction.py中给出。 如果运行代码，则将获得26作为输出，接近实际值，并确认我们的模型正在做出不错的预测。 您可以从数据文件中确认。

总结

在本章中，我们学习了集成学习及其在现实世界中的使用方式。 我们讨论了决策树以及如何基于决策树构建分类器。

我们了解了随机森林和极随机森林，它们是由多个决策树组成的。 我们讨论了如何基于它们构建分类器。 我们了解了如何估计预测的置信度。 我们还学习了如何处理类别失衡问题。

我们讨论了如何找到最佳训练参数以使用网格搜索来构建模型。 我们学习了如何计算相对特征的重要性。 然后，我们将集成学习技术应用于一个实际问题，在该问题中，我们使用一个非常随机的森林回归量来预测流量。

在下一章中，我们将讨论无监督学习以及如何检测股市数据中的模式。

7 通过无监督学习检测模式

在本章中，我们将学习无监督学习以及如何在现实世界中使用它。 到本章末，您将对以下主题有更好的理解：

• 无监督学习定义
• 使用 K 均值算法聚类数据
• 用均值漂移算法估计群集数
• 用轮廓分数估计聚类的质量
• 高斯混合模型
• 基于高斯混合模型构建分类器
• 使用相似性传播模型在股票市场中寻找子群体
• 根据购物模式细分市场

什么是无监督学习？

无监督学习是指不使用标记的训练数据而构建机器学习模型的过程。 无监督学习可在各种研究领域中找到应用，包括市场细分，股票市场，自然语言处理和计算机视觉等。

在前面的章节中，我们处理的是带有相关标签的数据。 在标记了训练数据之后，算法会学习根据这些标记对数据进行分类。 在现实世界中，标记数据可能并不总是可用。

有时，存在大量未加标签的数据，需要以某种方式对其进行分类。 这是无监督学习的完美用例。 无监督学习算法尝试使用某种相似性度量将数据分类到给定数据集中的子组中。

当我们有一个没有任何标签的数据集时，我们假定该数据是由于以某种方式控制分布的潜在变量而生成的。 然后可以从各个数据点开始以分级方式进行学习过程。 我们可以通过查找相似性的自然群集并尝试通过对数据进行分类和分段来获取信号和见解，从而为数据提供更深层次的表示。 让我们看看使用无监督学习对数据进行分类的一些方法。

使用 K 均值算法聚类数据

聚类是最流行的无监督学习技术之一。 此技术用于分析数据并在该数据中查找聚类。 为了找到这些聚类，我们使用相似性度量（例如欧几里得距离）来找到子组。 这种相似性度量可以估计群集的紧密度。 聚类是将数据组织到元素彼此相似的子组中的过程。

该算法的目标是识别使数据点属于同一子组的数据点的固有属性。 没有适用于所有情况的通用相似性指标。 例如，我们可能有兴趣查找每个子组的代表性数据点，或者我们有兴趣查找数据中的异常值。 根据情况，不同的指标可能比其他指标更合适。

K 均值算法是一种用于对数据进行聚类的众所周知的算法。 为了使用它，预先假定群集的数量。 使用各种数据属性将数据分为K子组。 群集的数量是固定的，并且根据该数量对数据进行分类。 这里的主要思想是我们需要在每次迭代时更新质心的位置。 重心是代表群集中心的位置。 我们继续进行迭代，直到将质心放置在其最佳位置。

我们可以看到质心的初始位置在算法中起着重要的作用。 这些质心应该以巧妙的方式放置，因为这会直接影响结果。 一个好的策略是将它们放置在尽可能远的距离。

基本的 K 均值算法将这些质心随机放置在K-Means++从数据点的输入列表中从算法上选择这些点的位置。 它试图使初始质心彼此远离，以便它们快速收敛。 然后，我们遍历训练数据集并将每个数据点分配给最接近的质心。

一旦我们遍历了整个数据集，第一次迭代就结束了。 这些点已根据初始化的质心进行了分组。 根据在第一次迭代结束时获得的新群集重新计算质心的位置。 一旦获得一组新的K重心，便会重复该过程。 我们遍历数据集并将每个点分配给最近的质心。

随着步骤不断重复，质心继续移动到其平衡位置。 经过一定数量的迭代后，质心不再更改其位置。 重心会聚到最终位置。 这些K重心是将用于推断的值。

让我们对二维数据应用 K 均值聚类，以了解其工作原理。 我们将使用提供给您的data_clustering.txt文件中的数据。 每行包含两个逗号分隔的数字。

创建一个新的 Python 文件并导入以下包：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn import metrics 

从文件中加载输入数据：

# Load input data
X = np.loadtxt('data_clustering.txt', delimiter=',') 

在应用 K 均值算法之前定义群集数：

num_clusters = 5 

可视化输入数据以查看展开图的样子：

# Plot input data
plt.figure()
plt.scatter(X[:,0], X[:,1], marker='o', facecolors='none',
        edgecolors='black', s=80)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
plt.title('Input data')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(()) 

可以看出该数据中有五个组。 使用初始化参数创建KMeans对象。 init参数表示选择群集的初始中心的初始化方法。 而不是随机选择它们，我们使用k-means++以更智能的方式选择这些中心。 这样可以确保算法快速收敛。 n_clusters参数是指群集数。 n_init参数是指算法在确定最佳结果之前应运行的次数：

# Create KMeans object
kmeans = KMeans(init='k-means++', n_clusters=num_clusters, n_init=10) 

使用输入数据训练 K 均值模型：

# Train the KMeans clustering model 
kmeans.fit(X) 

为了可视化边界，我们需要创建一个点网格并在所有这些点上评估模型。 让我们定义这个网格的步长：

# Step size of the mesh 
step_size = 0.01 

我们定义点的网格，并确保我们覆盖了输入数据中的所有值：

# Define the grid of points to plot the boundaries
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
x_vals, y_vals = np.meshgrid(np.arange(x_min, x_max, step_size),
        np.arange(y_min, y_max, step_size)) 

使用训练好的 K 均值模型预测网格上所有点的输出：

# Predict output labels for all the points on the grid
output = kmeans.predict(np.c_[x_vals.ravel(), y_vals.ravel()]) 

绘制所有输出值并为每个区域着色：

# Plot different regions and color them
output = output.reshape(x_vals.shape)
plt.figure()
plt.clf()
plt.imshow(output, interpolation='nearest', 
           extent=(x_vals.min(), x_vals.max(),
               y_vals.min(), y_vals.max()),
           cmap=plt.cm.Paired,
           aspect='auto',
           origin='lower') 

在这些有色区域上方叠加输入数据点：

# Overlay input points
plt.scatter(X[:,0], X[:,1], marker='o', facecolors='none',
        edgecolors='black', s=80) 

绘制使用 K 均值算法获得的聚类中心：

# Plot the centers of clusters
cluster_centers = kmeans.cluster_centers_
plt.scatter(cluster_centers[:,0], cluster_centers[:,1], 
        marker='o', s=210, linewidths=4, color='black', 
        zorder=12, facecolors='black')
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
plt.title('Boundaries of clusters')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
plt.show() 

完整的代码在kmeans.py文件的中给出。 如果运行代码，您将看到两个屏幕截图。 第一个屏幕截图是输入数据：

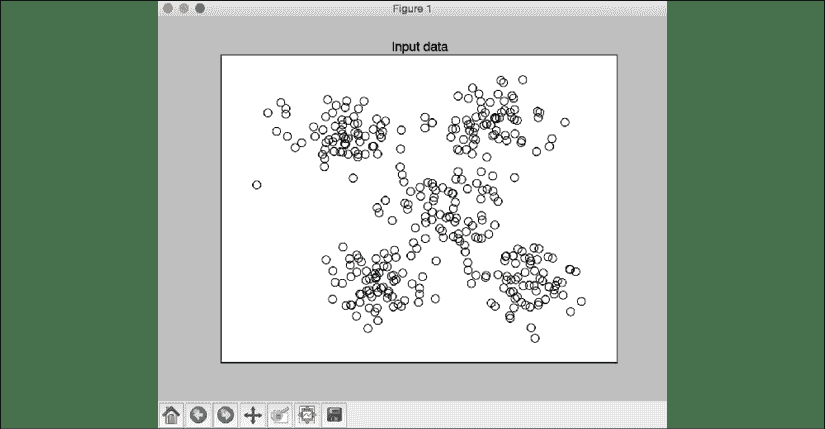
图 1：可视化输入数据

第二个屏幕截图表示使用 K 均值获得的边界：

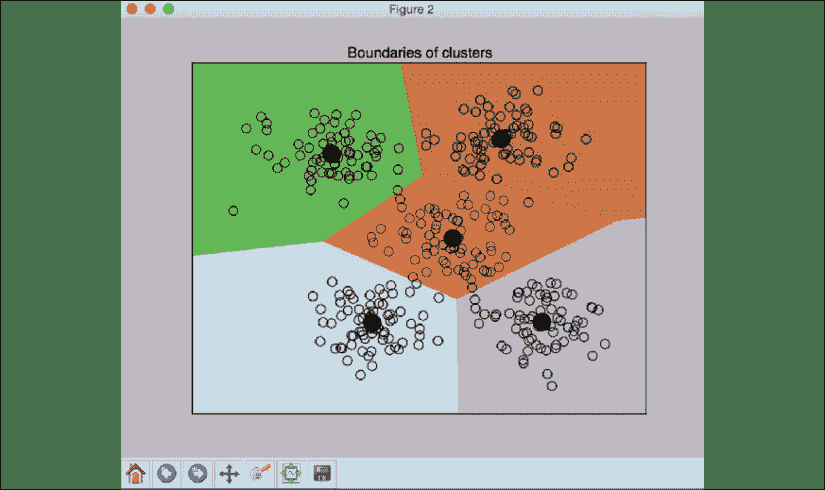
图 2：K 均值边界

每个群集中心的黑色填充圆圈表示该群集的质心。

涵盖了 K 均值算法之后，我们现在将继续另一种方法：MeanShift 算法。

使用均值漂移算法估计群集数

均值漂移是用于无监督学习的功能强大的算法。 这是一种经常用于聚类的非参数算法。 它是非参数的，因为它不对基础分布进行任何假设。 这与参量技术形成对比，参量技术假定基础数据遵循标准概率分布。 MeanShift 在对象跟踪和实时数据分析等领域中找到了许多应用。

在均值漂移算法中，整个特征空间被视为概率密度函数。 我们从训练数据集开始，并假设它是从概率密度函数中采样的。

在此框架中，聚类对应于基础分布的局部最大值。 如果存在K个群集，则基础数据分布中存在K个峰，均值漂移将识别这些峰。

MeanShift 的目标是识别质心的位置。 对于训练数据集中的每个数据点，它在其周围定义一个窗口。 然后，它为此窗口计算质心，并将位置更新为该新质心。 然后，通过在新位置周围定义一个窗口，对该新位置重复该过程。 随着我们不断这样做，我们将更接近群集的峰值。 每个数据点都将移向其所属的群集。 运动正朝着更高密度的区域发展。

重心（也称为均值）不断移向每个群集的峰。 该算法的名字源于手段不断变化的事实。 这种变化一直持续到算法收敛为止，在此阶段，质心不再移动。

让我们看看如何使用MeanShift估计给定数据集中的最佳群集数。 data_clustering.txt文件中的数据将用于分析。 该文件与“使用 K 均值算法聚类数据”部分中使用的文件相同。

创建一个新的 Python 文件并导入以下包：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import MeanShift, estimate_bandwidth
from itertools import cycle 

加载输入数据：

# Load data from input file
X = np.loadtxt('data_clustering.txt', delimiter=',') 

估计输入数据的带宽。 带宽是 MeanShift 算法中使用的底层核密度估计过程的参数。 带宽会影响算法的整体收敛速度，并最终影响最终的群集数。 因此，这是一个关键参数-如果带宽太小，可能会导致群集过多，而如果值太大，则会合并不同的群集。

quantile参数影响估计带宽的方式。 分位数的较高值将增加估计的带宽，从而导致较少的群集：

# Estimate the bandwidth of X
bandwidth_X = estimate_bandwidth(X, quantile=0.1, n_samples=len(X)) 

然后使用估计的带宽训练均值漂移聚类模型：

# Cluster data with MeanShift
meanshift_model = MeanShift(bandwidth=bandwidth_X, bin_seeding=True)
meanshift_model.fit(X) 

提取所有群集的中心：

# Extract the centers of clusters
cluster_centers = meanshift_model.cluster_centers_
print('\nCenters of clusters:\n', cluster_centers) 

提取集群数：

# Estimate the number of clusters 
labels = meanshift_model.labels_
num_clusters = len(np.unique(labels))
print("\nNumber of clusters in input data =", num_clusters) 

可视化和数据点：

# Plot the points and cluster centers
plt.figure()
markers = 'o*xvs'
for i, marker in zip(range(num_clusters), markers):
    # Plot points that belong to the current cluster
    plt.scatter(X[labels==i, 0], X[labels==i, 1], marker=marker, color='black') 

绘制当前群集的中心：

 # Plot the cluster center 
    cluster_center = cluster_centers[i]
    plt.plot(cluster_center[0], cluster_center[1], marker='o',  
            markerfacecolor='black', markeredgecolor='black',
            markersize=15)
plt.title('Clusters')
plt.show() 

完整代码在mean_shift.py文件中给出。 如果运行代码，您将看到以下屏幕快照，代表群集及其中心：

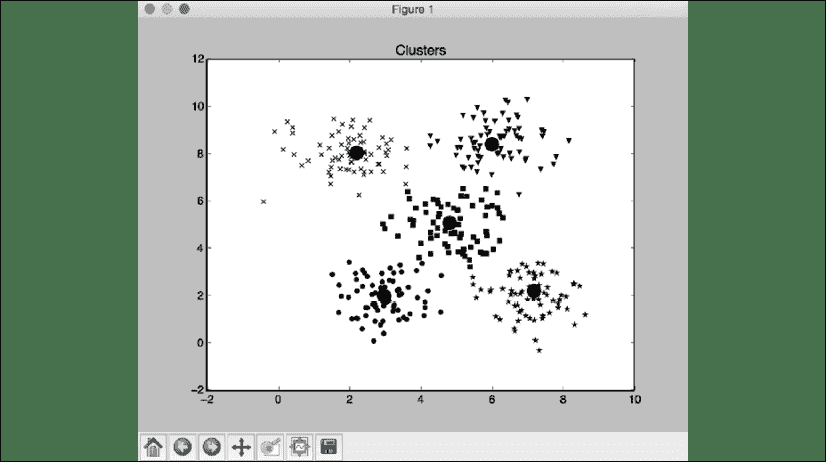
图 3：聚类图的中心

您将看到以下输出：：

图 4：集群输出的中心

至此，我们完成了均值漂移的概述。 到目前为止，我们已经讨论了如何对数据进行聚类。 接下来，我们将继续介绍如何使用轮廓方法估计聚类的质量。

使用轮廓分数估计聚类的质量

如果数据自然地组织成几个不同的群集，那么很容易在视觉上对其进行检查并得出一些推论。 不幸的是，在现实世界中很少如此。 现实世界中的数据庞大而混乱。 因此，我们需要一种量化聚类质量的方法。

轮廓是指用于检查数据中群集一致性的方法。 它提供了每个数据点与其群集的融合程度的估计。 轮廓分数是衡量数据点与其自身群集（与其他群集相比）的相似性的度量。 轮廓分数适用于任何相似度指标。

对于每个数据点，使用以下公式计算轮廓分数：

轮廓分数 = (p – q) / max(p, q)

这里，p是到数据点不属于的最近群集中各点的平均距离，q是到所有点的平均群集内距离在其自己的群集中。

轮廓分数范围的值在-1和1之间。 接近1的分数表示该数据点与群集中的其他数据点非常相似，而接近-1的分数指示该数据点与集群中其他数据点不同。 一种思考的方法是，如果有太多带有负轮廓分数的点，那么数据中的群集可能太少或太多。 我们需要再次运行聚类算法以找到最佳数目的聚类。 理想情况下，我们希望具有较高的正值。 根据业务问题，我们不需要优化并具有尽可能高的值，但是通常，如果我们的轮廓得分接近1，则表明数据可以很好地聚类。 如果分数接近-1，则表明我们用于分类的变量有噪声，并且不包含太多信号。

让我们看看如何使用轮廓分数来估计聚类表现。 创建一个新的 Python 文件并导入以下包：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics
from sklearn.cluster import KMeans 

我们将使用提供给您的data_quality.txt文件中的数据。 每行包含两个逗号分隔的数字：

# Load data from input file
X = np.loadtxt('data_quality.txt', delimiter=',') 

初始化变量。 values数组将包含一个值列表，以进行迭代并找到最佳群集数：

# Initialize variables
scores = []
values = np.arange(2, 10) 

遍历所有值并在每次迭代期间构建 K 均值模型：

# Iterate through the defined range 
for num_clusters in values:
    # Train the KMeans clustering model
    kmeans = KMeans(init='k-means++', n_clusters=num_clusters, n_init=10) 
    kmeans.fit(X) 

使用欧几里德距离度量来估计当前聚类模型的轮廓分数：

 score = metrics.silhouette_score(X, kmeans.labels_,
                metric='euclidean', sample_size=len(X)) 

打印轮廓分数作为当前值：

 print("\nNumber of clusters =", num_clusters) 
    print("Silhouette score =", score)

    scores.append(score) 

可视化轮廓分数的各种值：

# Plot silhouette scores 
plt.figure()
plt.bar(values, scores, width=0.7, color='black', align='center') 
plt.title('Silhouette score vs number of clusters') 

提取最佳分数和集群数量的相应值：

# Extract best score and optimal number of clusters 
num_clusters = np.argmax(scores) + values[0] 
print('\nOptimal number of clusters =', num_clusters) 

可视化输入数据：

# Plot data
plt.figure()
plt.scatter(X[:,0], X[:,1], color='black', s=80, marker='o', facecolors='none')
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
plt.title('Input data')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(()) 

plt.show() 

完整代码在文件clustering_quality.py中给出。 如果运行代码，您将看到两个屏幕截图。 第一个屏幕截图是输入数据：

图 5：可视化输入数据

我们可以看到，数据中有六个群集。 第二张屏幕截图代表了群集数的各种值的得分：

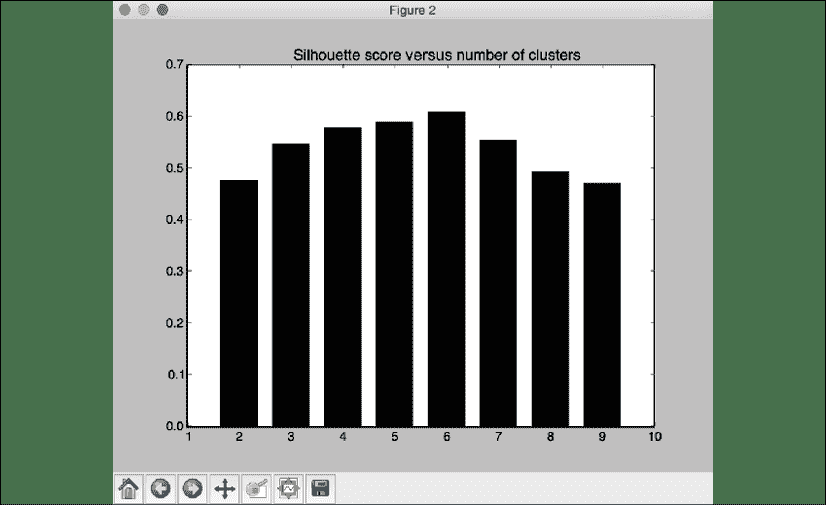
图 6：轮廓得分与群集数的关系

我们可以验证轮廓分数在0.6的值处达到峰值，这与数据一致。 您将看到以下输出：

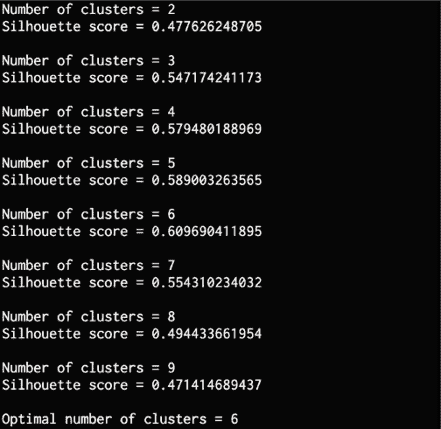
图 7：最佳集群输出

在本节中，我们了解了轮廓分数以及它们如何帮助我们理解聚类。 现在，我们将学习高斯混合模型，这是用于简化和聚类数据的另一种无监督学习技术。

什么是高斯混合模型？

在讨论高斯混合模型（GMM）之前，让我们首先了解什么是混合模型。 混合模型是一种概率密度模型，其中假定数据由几种成分分布控制。 如果这些分布是高斯分布，则该模型将变为高斯混合模型。 组合这些成分分布以提供多峰密度函数，该函数成为混合模型。

让我们看一个示例，以了解混合模型如何工作。 我们要模拟南美所有人的购物习惯。 做到这一点的一种方法是对整个大陆进行建模，然后将所有内容拟合为一个模型，但是不同国家/地区的人购物方式不同。 因此，我们需要了解各个国家/地区的人们如何购物以及他们的行为方式。

为了获得良好的代表性模型，我们需要考虑非洲大陆内的所有变化。 在这种情况下，我们可以使用混合模型来建模各个国家/地区的购物习惯，然后将它们全部组合成一个混合模型。

这样，就不会错过各个国家基本行为数据中的细微差别。 通过不在所有国家/地区实现单一模型，可以创建更准确的模型。

需要注意的有趣一点是，混合模型是半参数的，这意味着它们部分依赖于一组预定义的函数。 它们可以为数据的基础分布建模提供更高的精度和灵活性。 它们可以消除因稀疏数据而导致的差距。

定义函数后，混合模型将从半参数变为参数。 因此， GMM 是一个参数模型，表示为分量高斯函数的加权和。 我们假设数据是由一组以某种方式组合的高斯模型生成的。 GMM 非常强大，并用于许多领域。 GMM 的参数是使用算法（例如期望最大化（EM）或最大后验概率（MAP）估计。 GMM inc 的一些流行应用包括图像数据库检索，股票市场波动建模，生物特征验证等。

现在我们已经描述了什么是 GMM，让我们看看如何应用它们。

基于高斯混合模型构建分类器

让我们基于高斯混合模型构建分类器。 创建一个新的 Python 文件并导入以下包：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import patches 

from sklearn import datasets 
from sklearn.mixture import GaussianMixture 
from sklearn.model_selection import StratifiedKFold
from sklearn.model_selection import train_test_split 

让我们使用 scikit-learn 中可用的鸢尾花数据集进行分析：

# Load the iris dataset 
iris = datasets.load_iris() 

X, y = datasets.load_iris(return_X_y=True) 

使用 80/20 拆分将数据集拆分为训练和测试。 n_splits参数指定您将获得的子集数。 我们使用5的值，这意味着数据集将分为五个部分。

我们将使用四个部分来进行训练，使用一个部分来进行测试，从而得出 80/20 的比例：

# Split dataset into training and testing (80/20 split)
skf = StratifiedKFold(n_splits=5) # 
skf.get_n_splits(X, y) 

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=0) 

提取训练数据中的类别数量：

# Extract the number of classes 
num_classes = len(np.unique(y_train)) 

使用相关参数构建基于 GMM 的分类器。 n_components参数指定基础分发中的组件数。 在这种情况下，它将是数据中不同类的数量。 我们需要指定要使用的协方差类型。 在这种情况下，将使用完全协方差。 init_params参数控制在训练过程中需要更新的参数。 使用kmeans值，这意味着权重和协方差参数将在训练期间更新。 max_iter参数是指训练期间将执行的期望最大化迭代次数：

# Build GMM
classifier = GaussianMixture(n_components=num_classes, covariance_type='full',init_params='kmeans', max_iter=20) 

初始化分类器的方法：

# Initialize the GMM means
classifier.means_ = np.array([X_train[y_train == i].mean(axis=0) 
for i in range(num_classes)])

使用训练数据训练高斯混合模型分类器：

# Train the GMM classifier
classifier.fit(X_train) 

可视化分类器的边界。 然后提取特征值和特征向量，以估计如何在群集周围绘制椭圆边界。 有关特征值和特征向量的快速更新，请参阅这里。 让我们继续进行以下绘制：

# Draw boundaries
plt.figure()
colors = 'bgr'
for i, color in enumerate(colors):
    # Extract eigenvalues and eigenvectors
    eigenvalues, eigenvectors = np.linalg.eigh(
            classifier.covariances_[i][:2, :2]) 

归一化第一个特征向量：

 # Normalize the first eigenvector
    norm_vec = eigenvectors[0] / np.linalg.norm(eigenvectors[0]) 

椭圆需要旋转以准确显示分布。 估计角度：

 # Extract the angle of tilt
    angle = np.arctan2(norm_vec[1], norm_vec[0])
    angle = 180 * angle / np.pi 

放大椭圆以进行可视化。 特征值控制椭圆的大小：

 # Scaling factor to magnify the ellipses 
    # (random value chosen to suit our needs) 
    scaling_factor = 8
    eigenvalues *= scaling_factor 

绘制椭圆：

 # Draw the ellipse
    ellipse = patches.Ellipse(classifier.means_[i, :2],
            eigenvalues[0], eigenvalues[1], 180 + angle,
            color=color)
    axis_handle = plt.subplot(1, 1, 1)
    ellipse.set_clip_box(axis_handle.bbox)
    ellipse.set_alpha(0.6)
    axis_handle.add_artist(ellipse) 

在图上叠加输入数据：

# Plot the data
colors = 'bgr'
for i, color in enumerate(colors): 
    cur_data = iris.data[iris.target == i]
    plt.scatter(cur_data[:,0], cur_data[:,1], marker='o',
            facecolors='none', edgecolors='black', s=40,
            label=iris.target_names[i]) 

在此图上叠加测试数据：

 test_data = X_test[y_test == i]  
    plt.scatter(test_data[:,0], test_data[:,1], marker='s',
            facecolors='black', edgecolors='black', s=40 ,
            label=iris.target_names[i]) 

计算训练和测试数据的预测输出：

# Compute predictions for training and testing data
y_train_pred = classifier.predict(X_train)
accuracy_training = np.mean(y_train_pred.ravel() == y_train.ravel()) * 100 
print('Accuracy on training data =', accuracy_training) 

y_test_pred = classifier.predict(X_test)
accuracy_testing = np.mean(y_test_pred.ravel() == y_test.ravel()) * 100 
print('Accuracy on testing data =', accuracy_testing) 

plt.title('GMM classifier')
plt.xticks(())
plt.yticks(()) 

plt.show() 

完整代码在文件gmm_classifier.py中给出。 运行代码后，您将看到以下输出：

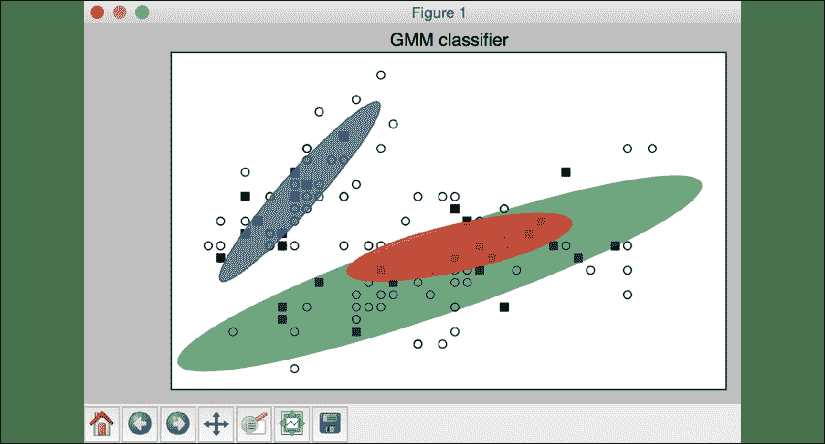
图 8：高斯混合模型分类器图

输入的数据由三个分布组成。 不同大小和角度的三个椭圆表示输入数据中的基础分布。 您将看到以下输出：

Accuracy on training data = 87.5
Accuracy on testing data = 86.6666666667 

在本节中，我们学习了高斯混合模型，并使用 Python 开发了一个示例。 在下一节中，我们将学习另一种无监督学习技术，即相似性传播模型，用于对数据进行分类，并将其用于 ，以便在股市数据中查找子组。

使用“相似性传播”模型在股票市场中寻找子群体

相似性传播是一种聚类算法，不需要事先指定多个聚类。 由于其通用性和实现的简便性，它已在许多领域中找到了许多应用。 它使用一种称为消息传递的技术找出代表性的群集，称为样本。 它从指定需要考虑的相似性度量开始。 同时将所有训练数据点视为潜在的范例。 然后，它在数据点之间传递消息，直到找到一组示例为止。

消息传递发生在两个备用步骤中，分别称为责任和可用性。 责任是指从群集成员发送到候选示例的消息，指示该数据点作为该示例群集的成员的适合程度。 可用性是指从候选示例发送到集群的潜在成员的消息，表明它作为示例的适用性。 一直执行此操作，直到算法收敛到最佳样本集为止。

还有一个称为首选项的参数，该参数控制将发现的示例数量。 如果选择较高的值，则将导致算法找到太多的聚类。 如果选择一个较低的值，则将导致少数群集。 最佳值是点之间的中间相似度。

让我们使用“相似性传播”模型来查找股票市场中的子组。 我们将使用开盘价和收盘价之间的股票报价变化作为控制特征。 创建一个新的 Python 文件并导入以下包：

import datetime
import json
import numpy as np
import matplotlib.pyplot as plt
from sklearn import covariance, cluster
import yfinance as yf 

matplotlib 中可用的股市数据将用作输入。 公司符号在文件company_symbol_mapping.json中映射到其全名：

# Input file containing company symbols 
input_file = 'company_symbol_mapping.json' 

从文件中加载公司符号图：

# Load the company symbol map
with open(input_file, 'r') as f:
    company_symbols_map = json.loads(f.read()) 

symbols, names = np.array(list(company_symbols_map.items())).T 

从 matplotlib 加载股票报价：

# Load the historical stock quotes 
start_date = datetime.datetime(2019, 1, 1)
end_date = datetime.datetime(2019, 1, 31)
quotes = [yf.Ticker(symbol).history(start=start_date, end=end_date)
                for symbol in symbols] 

计算开始和结束报价之间的差异：

# Extract opening and closing quotes 
opening_quotes = np.array([quote.Open for quote in quotes]).astype(np.float)
closing_quotes = np.array([quote.Close for quote in quotes]).astype(np.float) 

# Compute differences between opening and closing quotes
quotes_diff = closing_quotes - opening_quotes 

规范化数据：

# Normalize the data
X = quotes_diff.copy().T
X /= X.std(axis=0) 

创建一个图模型：

# Create a graph model
edge_model = covariance.GraphLassoCV() 

训练模型：

# Train the model
with np.errstate(invalid='ignore'): 
    edge_model.fit(X) 

使用我们刚刚训练的边缘模型构建相似性传播聚类模型：

# Build clustering model using Affinity Propagation model
_, labels = cluster.affinity_propagation(edge_model.covariance_)
num_labels = labels.max() 

打印输出：

# Print the results of clustering
print('\nClustering of stocks based on difference in opening and closing quotes:\n')
for i in range(num_labels + 1):
    print("Cluster", i+1, "==>", ', '.join(names[labels == i])) 

完整代码在文件stocks.py中给出。 运行代码时，您将看到以下输出：

图 9：基于开盘价和收盘价差异的股票聚类

此输出代表该时间段内股票市场中的各个子组。 请注意，运行代码时群集可能会以不同的顺序出现。

既然我们已经了解了“相似性传播”模型并学习了一些新概念，我们将继续本章的最后部分，在此部分中，我们将使用无监督学习技术，根据客户的购物习惯来细分市场数据。

根据购物模式细分市场

让我们看看如何运用无监督学习技术根据客户的购物习惯来细分市场。 为您提供了一个名为sales.csv的文件。 该文件包含来自多家零售服装店的各种上衣的销售详细信息。 目标是确定模式并根据这些商店中售出的商品数量来细分市场。

创建一个新的 Python 文件并导入以下包：

import csv 

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import MeanShift, estimate_bandwidth 

从输入文件加载数据。 由于它是 CSV 文件，因此我们可以在 Python 中使用 csv 阅读器从该文件中读取数据并将其转换为NumPy数组：

# Load data from input file
input_file = 'sales.csv'
file_reader = csv.reader(open(input_file, 'r'), delimiter=',')
X = []
for count, row in enumerate(file_reader): 
    if not count:
        names = row[1:]
        continue 

 X.append([float(x) for x in row[1:]]) 

# Convert to numpy array
X = np.array(X) 

让我们估计输入数据的带宽：

# Estimating the bandwidth of input data
bandwidth = estimate_bandwidth(X, quantile=0.8, n_samples=len(X)) 

根据估计的带宽训练平均漂移模型：

# Compute clustering with MeanShift
meanshift_model = MeanShift(bandwidth=bandwidth, bin_seeding=True)
meanshift_model.fit(X) 

提取标签和每个群集的中心：

labels = meanshift_model.labels_
cluster_centers = meanshift_model.cluster_centers_ 
num_clusters = len(np.unique(labels)) 

打印集群数和集群中心：

print("\nNumber of clusters in input data =", num_clusters) 

print("\nCenters of clusters:")
print('\t'.join([name[:3] for name in names]))
for cluster_center in cluster_centers:
    print('\t'.join([str(int(x)) for x in cluster_center])) 

我们正在处理六维数​​据。 为了使数据可视化，让我们使用由第二维和第三维构成的二维数据：

# Extract two features for visualization 
cluster_centers_2d = cluster_centers[:, 1:3] 

绘制群集的中心：

# Plot the cluster centers
plt.figure()
plt.scatter(cluster_centers_2d[:,0], cluster_centers_2d[:,1],
        s=120, edgecolors='black', facecolors='none') 

offset = 0.25
plt.xlim(cluster_centers_2d[:,0].min() - offset * cluster_centers_2d[:,0].ptp(),
        cluster_centers_2d[:,0].max() + offset * cluster_centers_2d[:,0].ptp(),)
plt.ylim(cluster_centers_2d[:,1].min() - offset * cluster_centers_2d[:,1].ptp(),
        cluster_centers_2d[:,1].max() + offset * cluster_centers_2d[:,1].ptp())
plt.title('Centers of 2D clusters') 

plt.show() 

文件market_segmentation.py中提供了完整代码。 运行代码时，您将看到以下输出：

图 10：2D 群集的中心图

在本章的最后一部分中，我们应用了在本章前面了解的均值漂移算法，并将其用于分析和细分客户的使用习惯。

您还将看到以下输出：

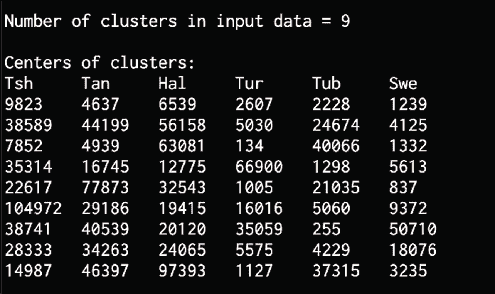
图 11：集群中心输出

总结

在本章中，我们首先讨论无监督学习及其应用。 然后，我们学习了聚类以及如何使用 K 均值算法聚类数据。 我们讨论了如何使用均值漂移算法估计聚类数。 我们讨论了轮廓分数以及如何估计聚类的质量。 我们了解了高斯混合模型，以及如何基于它们建立分类器。 我们还讨论了“亲和力传播”模型，并使用它在股票市场中找到了子组。 然后，我们应用均值漂移算法根据购物模式细分市场。

在下一章中，我们将学习如何构建推荐引擎。

8 构建推荐系统

在本章中，我们将学习如何建立一个推荐系统来推荐人们可能喜欢看的电影。 我们将了解 K 最近邻分类器，并了解如何实现它。 我们使用这些概念来讨论协同过滤，然后使用它来构建推荐系统。

到本章末，您将了解以下内容：

• 提取最近邻
• 建立 K 最近邻分类器
• 计算相似度分数
• 使用协同过滤查找相似用户
• 建立电影推荐系统

提取最近邻

推荐人系统采用最近邻的概念来找到好的建议。 名称最近邻是指从给定数据集中查找到输入点最近的数据点的过程。 这通常用于构建分类系统，该分类系统根据输入数据点与各种类别的接近程度对数据点进行分类。 让我们看看如何找到给定数据点的最近邻。

首先，创建一个新的 Python 文件并导入以下包：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import NearestNeighbors 

定义样本 2D 数据点：

# Input data
X = np.array([[2.1, 1.3], [1.3, 3.2], [2.9, 2.5], [2.7, 5.4], [3.8, 0.9], 
        [7.3, 2.1], [4.2, 6.5], [3.8, 3.7], [2.5, 4.1], [3.4, 1.9],
        [5.7, 3.5], [6.1, 4.3], [5.1, 2.2], [6.2, 1.1]]) 

定义要提取的最近邻的数量：

# Number of nearest neighbors
k = 5 

定义一个测试数据点，该数据点将用于提取最近的 K 个邻居：

# Test data point 
test_data_point = [4.3, 2.7] 

使用圆形黑色标记绘制输入数据：

# Plot input data
plt.figure()
plt.title('Input data')
plt.scatter(X[:,0], X[:,1], marker='o', s=75, color='black') 

使用输入数据创建并训练 K 近邻模型。 使用此模型提取到测试数据点最近邻：

# Build K Nearest Neighbors model
knn_model = NearestNeighbors(n_neighbors=k, algorithm='ball_tree').fit(X) 
distances, indices = knn_model.kneighbors(test_data_point) 

打印从模型中提取的最近邻：

# Print the 'k' nearest neighbors
print("\nK Nearest Neighbors:")
for rank, index in enumerate(indices[0][:k], start=1):
    print(str(rank) + " ==>", X[index]) 

可视化最近邻：

# Visualize the nearest neighbors along with the test datapoint
plt.figure()
plt.title('Nearest neighbors')
plt.scatter(X[:, 0], X[:, 1], marker='o', s=75, color='k')
plt.scatter(X[indices][0][:][:, 0], X[indices][0][:][:, 1],
        marker='o', s=250, color='k', facecolors='none')
plt.scatter(test_data_point[0], test_data_point[1],
        marker='x', s=75, color='k') 

plt.show() 

完整代码在文件k_nearest_neighbors.py中给出。 如果运行代码，您将看到两个屏幕截图。 第一个屏幕截图表示输入数据：

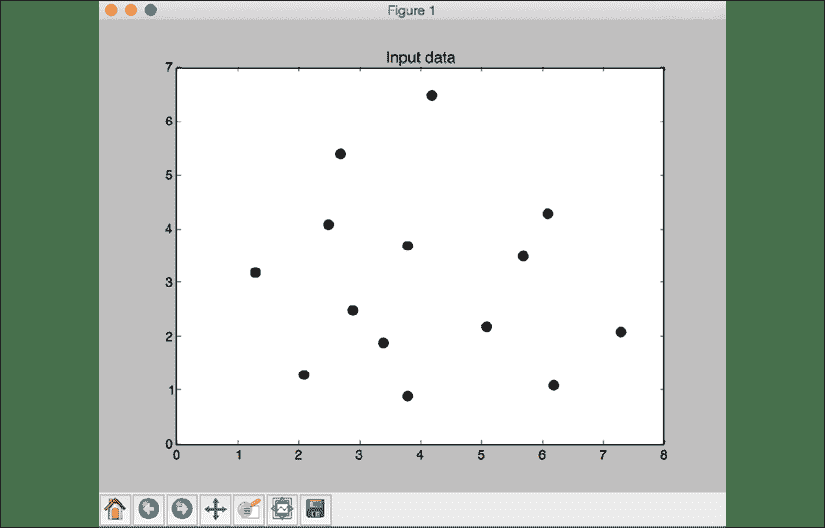
图 1：输入数据集的可视化

第二张屏幕截图代表五个最近邻。 使用十字显示测试数据点，并圈出最近邻点：

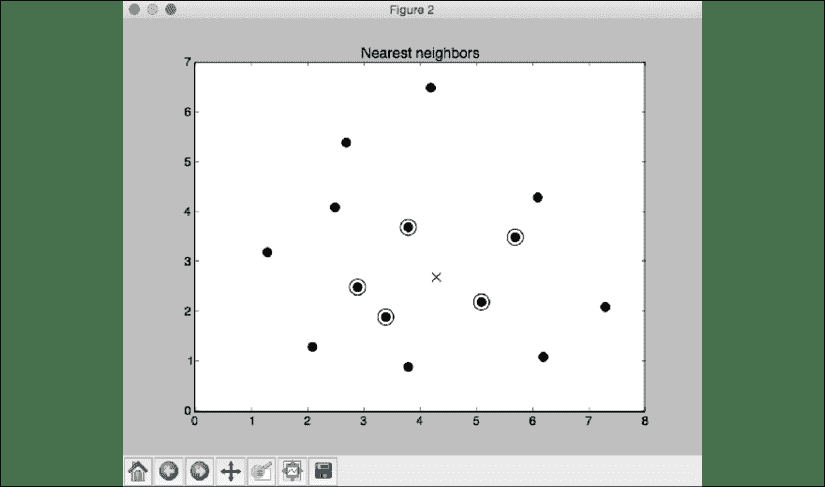
图 2：五个最近邻图

您将看到以下输出：

图 3：K 近邻输出

上图显示了最接近测试数据点的五个点。 现在我们已经学习了如何构建和运行 K 近邻模型，在下一节中，我们将基于该知识并使用它来构建 K 近邻分类器。

建立 K 最近邻分类器

K 近邻分类器是使用 K 近邻算法对给定数据点进行分类的分类模型。 该算法在训练数据集中找到最接近的K个数据点，以识别输入数据点的类别。 然后，它将基于多数投票为该数据点分配一个类别。 从这些K数据点的列表中，我们查看相应的类别，然后选择投票数最高的类别。K的值取决于当前的问题。 让我们看看如何使用此模型构建分类器。

创建一个新的 Python 文件并导入以下包：

import numpy as np
import matplotlib.pyplot as plt 
import matplotlib.cm as cm
from sklearn import neighbors, datasets 

从data.txt加载输入数据。 每行包含逗号分隔的值，数据包含四个类别：

# Load input data
input_file = 'data.txt'
data = np.loadtxt(input_file, delimiter=',')
X, y = data[:, :-1], data[:, -1].astype(np.int) 

使用四种不同的标记形状可视化输入数据。 我们需要将标签映射到相应的标记，这是mapper变量进入图片的位置：

# Plot input data
plt.figure()
plt.title('Input data')
marker_shapes = 'v^os'
mapper = [marker_shapes[i] for i in y]
for i in range(X.shape[0]):
    plt.scatter(X[i, 0], X[i, 1], marker=mapper[i],
            s=75, edgecolors='black', facecolors='none') 

定义要使用的最近邻的数量：

# Number of nearest neighbors
num_neighbors = 12 

定义将用于可视化分类器模型边界的网格步长：

# Step size of the visualization grid
step_size = 0.01 

创建 K 最近邻分类器模型：

# Create a K Nearest Neighbors classifier model
classifier = neighbors.KNeighborsClassifier(num_neighbors, weights='distance') 

使用训练数据训练模型：

# Train the K Nearest Neighbors model
classifier.fit(X, y) 

创建将用于可视化网格的值的网格网格：

# Create the mesh to plot the boundaries
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
x_values, y_values = np.meshgrid(np.arange(x_min, x_max, step_size),
        np.arange(y_min, y_max, step_size)) 

在网格上的所有点上评估分类器，以创建边界的可视化效果：

# Evaluate the classifier on all the points on the grid
output = classifier.predict(np.c_[x_values.ravel(), y_values.ravel()]) 

创建一个彩色网格以可视化输出：

# Visualize the predicted output
output = output.reshape(x_values.shape)
plt.figure()
plt.pcolormesh(x_values, y_values, output, cmap=cm.Paired) 

将训练数据覆盖在此颜色网格上方，以可视化相对于边界的数据：

# Overlay the training points on the map 
for i in range(X.shape[0]):
    plt.scatter(X[i, 0], X[i, 1], marker=mapper[i],
            s=50, edgecolors='black', facecolors='none') 

设置X和Y限制以及标题：

plt.xlim(x_values.min(), x_values.max()) 
plt.ylim(y_values.min(), y_values.max())
plt.title('K Nearest Neighbors classifier model boundaries') 

定义测试数据点以查看分类器的表现。 创建一个包含训练数据点和测试数据点的图形，以查看其位置：

# Test input data point 
test_data_point = [5.1, 3.6]
plt.figure()
plt.title('Test data_point')
for i in range(X.shape[0]):
    plt.scatter(X[i, 0], X[i, 1], marker=mapper[i],
            s=75, edgecolors='black', facecolors='none') 

plt.scatter(test_data_point[0], test_data_point[1], marker='x', 
        linewidth=6, s=200, facecolors='black') 

根据分类器模型，将 K 最近邻提取到测试数据点：

# Extract the K nearest neighbors
_, indices = classifier.kneighbors([test_data_point])
indices = indices.astype(np.int)[0] 

画出在上一步中获得的 K 近邻邻居：

# Plot k nearest neighbors
plt.figure()
plt.title('K Nearest Neighbors') 

for i in indices:
    plt.scatter(X[i, 0], X[i, 1], marker=mapper[y[i]],
            linewidth=3, s=100, facecolors='black') 

覆盖测试数据点：

plt.scatter(test_data_point[0], test_data_point[1], marker='x',
        linewidth=6, s=200, facecolors='black') 

覆盖输入数据：

for i in range(X.shape[0]):
    plt.scatter(X[i, 0], X[i, 1], marker=mapper[i],
            s=75, edgecolors='black', facecolors='none') 

打印预测的输出：

print("Predicted output:", classifier.predict([test_data_point])[0]) 

plt.show() 

完整代码在文件nearest_neighbors_classifier.py中给出。 如果运行代码，您将看到四个屏幕截图。 第一个屏幕截图表示输入数据：

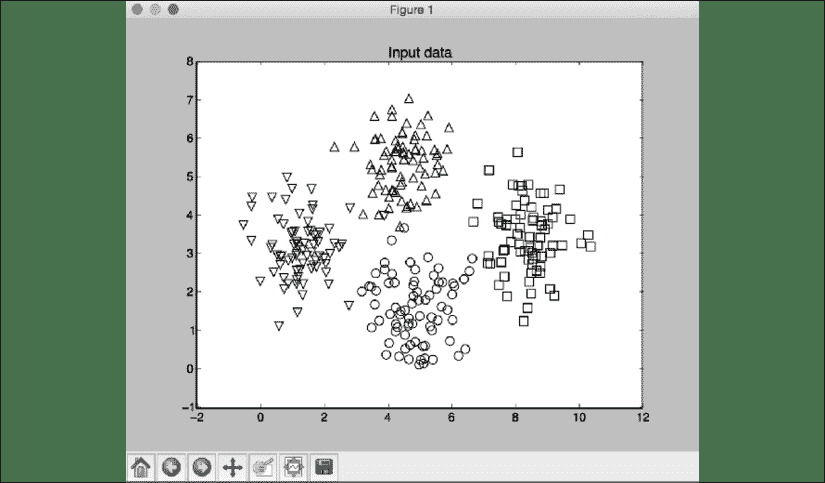
图 4：可视化输入数据

第二张屏幕截图表示分类器边界：

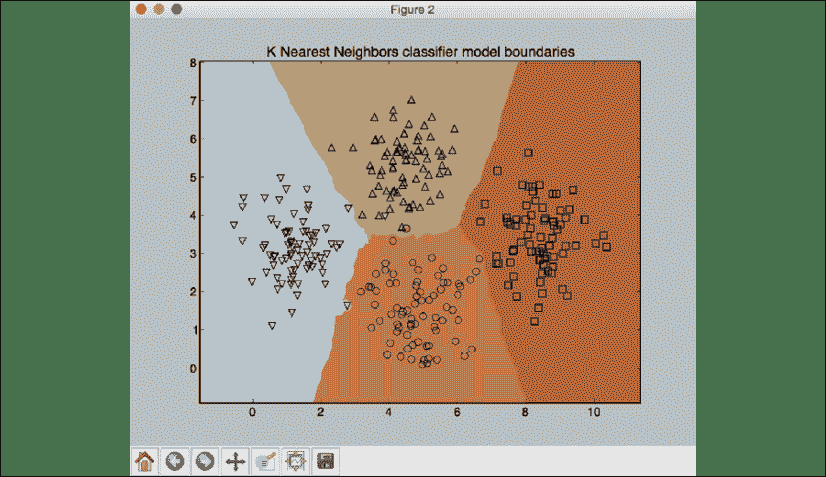
图 5：分类器模型边界

第三个屏幕截图显示了相对于输入数据集的测试数据点。 使用十字显示测试数据点：

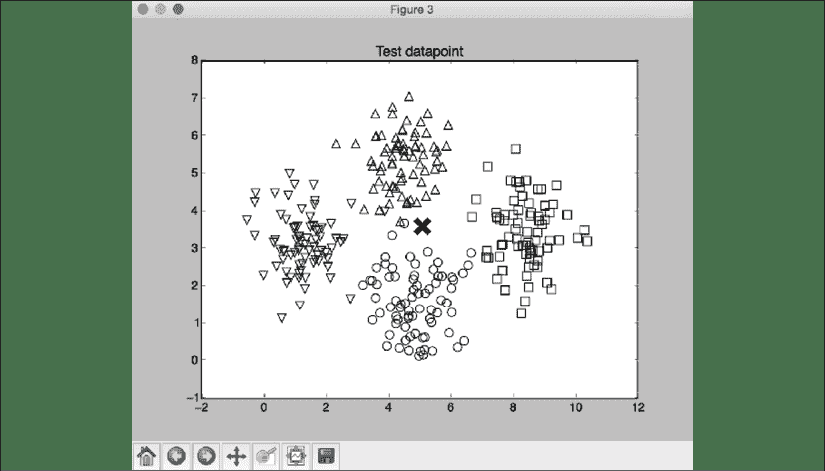
图 6：相对于输入数据集的测试数据点

第四个屏幕截图显示了距离测试数据点最近的 12 个邻居：

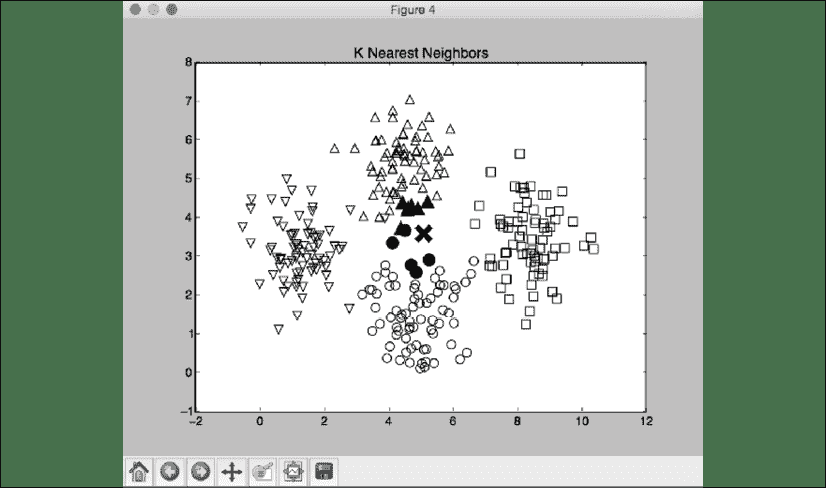
图 7：12 个最近邻图

您将看到以下输出，这表明模型正在预测测试数据点属于1类：

Predicted output: 1 

像任何机器学习模型一样，输出是一个预测，可能与实际结果相匹配。

计算相似度分数

要构建推荐系统，重要的是要了解如何比较数据集中的各种对象。 如果数据集由人物及其不同的电影喜好组成，那么为了提出建议，我们需要了解如何将任何两个人物相互比较。 这是相似度分数很重要的地方。 相似度得分给出了两个数据点相似度的想法。

此领域中经常使用两个分数-欧几里得分数和皮尔森分数。 欧几里得分数使用两个数据点之间的欧几里得距离来计算分数。 如果需要快速了解欧几里德距离的计算方式，则可以转到这里。

欧几里得距离的值可以是无界的。 因此，我们采用该值并将其转换为欧几里得分数从0到1的范围。 如果两个对象之间的欧几里得距离较大，则欧几里得分数应较低，因为低分数表明对象不相似。 因此，欧几里得距离与欧几里得分数成反比。

皮尔森分数是两个数据点之间相关性的度量。 它使用两个数据点之间的协方差以及它们各自的标准差来计算分数。 得分范围从-1到+1。 分数+1表示数据点相似，分数-1表示数据点相似。 分数0表示它们之间没有相关性。 让我们看看如何计算这些分数。

创建一个新的 Python 文件并导入以下包：

import argparse
import json
import numpy as np 

构建参数解析器以处理输入参数。 它将接受两个用户以及用于计算相似性得分所需的得分类型：

def build_arg_parser():
    parser = argparse.ArgumentParser(description='Compute similarity score')
    parser.add_argument('--user1', dest='user1', required=True,
            help='First user')
    parser.add_argument('--user2', dest='user2', required=True,
            help='Second user')
    parser.add_argument("--score-type", dest="score_type", required=True, 
            choices=['Euclidean', 'Pearson'], help='Similarity metric to be used')
    return parser 

定义一个函数来计算输入用户之间的欧几里得分数。 如果用户不在数据集中，则代码将引发错误：

# Compute the Euclidean distance score between user1 and user2 
def euclidean_score(dataset, user1, user2):
    if user1 not in dataset:
        raise TypeError('Cannot find ' + user1 + ' in the dataset') 

 if user2 not in dataset:
        raise TypeError('Cannot find ' + user2 + ' in the dataset') 

定义一个变量以跟踪两个用户都评价过的电影：

 # Movies rated by both user1 and user2 
    common_movies = {} 

提取两个用户都评价的电影：

 for item in dataset[user1]:
        if item in dataset[user2]:
            common_movies[item] = 1 

如果没有普通电影，则无法计算相似度得分：

 # If there are no common movies between the users, 
    # then the score is 0
    if len(common_movies) == 0:
        return 0 

计算等级之间的平方差异，并使用其计算欧几里得分数：

 squared_diff = [] 

 for item in dataset[user1]:
        if item in dataset[user2]:
            squared_diff.append(np.square(dataset[user1][item] - dataset[user2][item]))

    return 1 / (1 + np.sqrt(np.sum(squared_diff))) 

定义一个函数来计算给定数据集中用户之间的皮尔森得分。 如果在数据集中找不到用户，则会引发错误：

# Compute the Pearson correlation score between user1 and user2
def pearson_score(dataset, user1, user2):
    if user1 not in dataset:
        raise TypeError('Cannot find ' + user1 + ' in the dataset') 

 if user2 not in dataset:
        raise TypeError('Cannot find ' + user2 + ' in the dataset') 

定义一个变量以跟踪两个用户都评价过的电影：

 # Movies rated by both user1 and user2 
    common_movies = {} 

提取两个用户都评价的电影：

 for item in dataset[user1]:
        if item in dataset[user2]: 
            common_movies[item] = 1 

如果没有普通电影，那么我们将无法计算相似度得分：

 num_ratings = len(common_movies)
    # If there are no common movies between 
    #user1 and user2, then the score is 0 

 if num_ratings == 0:
        return 0 

计算两个用户都已评分的所有电影的评分总和：

 # Calculate the sum of ratings of all the common movies
    user1_sum = np.sum([dataset[user1][item] for item in common_movies]) 
    user2_sum = np.sum([dataset[user2][item] for item in common_movies]) 

计算两个用户都已评分的所有电影的评分的平方和：

 # Calculate the sum of squares of ratings 
    # of all the common movies  
    user1_squared_sum = np.sum([np.square(dataset[user1][item]) for item in common_movies])
    user2_squared_sum = np.sum([np.square(dataset[user2][item]) for item in common_movies]) 

计算两个输入用户都评价过的所有电影的评价结果​​的总和：

 # Calculate the sum of products of the 
    # ratings of the common movies 
    sum_of_products = np.sum([dataset[user1][item] * dataset[user2][item] for item in common_movies]) 

使用前面的计算来计算计算皮尔森分数所需的各种参数：

 # Calculate the Pearson correlation score
    Sxy = sum_of_products - (user1_sum * user2_sum / num_ratings) 
    Sxx = user1_squared_sum - np.square(user1_sum) / num_ratings 
    Syy = user2_squared_sum - np.square(user2_sum) / num_ratings 

如果没有偏差，则得分为0：

 if Sxx * Syy == 0: 

 return 0 

返回皮尔逊得分：

 return Sxy / np.sqrt(Sxx * Syy) 

定义main函数并解析输入参数：

if __name__=='__main__':
    args = build_arg_parser().parse_args() 
    user1 = args.user1
    user2 = args.user2 
    score_type = args.score_type 

将文件ratings.json中的评级加载到字典中：

 ratings_file = 'ratings.json' 

 with open(ratings_file, 'r') as f:
        data = json.loads(f.read()) 

根据输入参数计算相似度得分：

if score_type == 'Euclidean':
    print("\nEuclidean score:")
    print(euclidean_score(data, user1, user2))
else:
    print("\nPearson score:")
    print(pearson_score(data, user1, user2)) 

完整代码在文件compute_scores.py中给出。 让我们用一些组合来运行代码。 要计算David Smith和Bill Duffy之间的欧几里得分数：

$ python3 compute_scores.py --user1 "David Smith" --user2 "Bill Duffy" --score-type Euclidean 

如果运行前面的命令，将获得以下输出：

Euclidean score:
0.585786437627 

如果要计算同一对之间的皮尔逊得分，请运行以下命令：

$ python3 compute_scores.py --user1 "David Smith" --user2 "Bill Duffy" --score-type Pearson 

您将看到以下输出：

Pearson score:
0.99099243041 

也可以使用其他参数组合来运行。

在本节中，我们学习了如何计算相似性得分，并了解了为什么在推荐系统的构建中该重要因素。 在下一节中，我们将学习如何通过协同过滤来识别具有相似偏好的用户。

使用协同过滤查找相似用户

协同过滤是指在数据集中的对象之间标识模式以决定新对象的过程。 在推荐引擎的上下文中，协同过滤用于通过查看数据集中的相似用户来提供推荐。

通过收集数据集中不同用户的偏好，我们可以协作该信息来过滤用户。 因此，名称为协同过滤。

这里的假设是，如果两个人对一组电影的收视率相似，那么他们对一组新的未知电影的选择也将相似。 通过识别那些普通电影中的模式，可以对新电影做出预测。 在上一节中，我们学习了如何比较数据集中的不同用户。 现在将使用讨论的评分技术在数据集中查找相似的用户。 协同过滤算法可以并行化并在大数据系统（例如 AWS EMR 和 Apache Spark）中实现，从而能够处理数百 TB 的数据。 这些方法可用于各种垂直领域，例如金融，在线购物，市场营销，客户研究等。

让我们开始构建协同过滤系统。

创建一个新的 Python 文件并导入以下包：

import argparse
import json
import numpy as np 

from compute_scores import pearson_score 

定义一个函数来解析输入参数。 输入参数是用户的名称：

def build_arg_parser():
    parser = argparse.ArgumentParser(description='Find users who are similar to the input user')
    parser.add_argument('--user', dest='user', required=True, 
            help='Input user')
    return parser 

定义一个函数以在数据集中查找与给定用户相似的用户。 如果用户不在数据集中，则引发错误：

# Finds users in the dataset that are similar to the input user 
def find_similar_users(dataset, user, num_users):
    if user not in dataset:
        raise TypeError('Cannot find ' + user + ' in the dataset') 

计算皮尔森得分的函数已导入。 让我们使用该函数来计算输入用户与数据集中所有其他用户之间的皮尔森得分：

 # Compute Pearson score between input user 
    # and all the users in the dataset
    scores = np.array([[x, pearson_score(dataset, user,
            x)] for x in dataset if x != user]) 

分数按降序排列：

 # Sort the scores in decreasing order 
    scores_sorted = np.argsort(scores[:, 1])[::-1] 

提取输入参数指定的最高num_users个用户，并返回数组：

 # Extract the top 'num_users' scores 
    top_users = scores_sorted[:num_users] 

 return scores[top_users] 

定义main函数并解析输入参数以提取用户名：

if __name__=='__main__':
    args = build_arg_parser().parse_args() 
    user = args.user 

从电影分级文件ratings.json加载数据。 此文件包含人物名称及其对各种电影的评分：

 ratings_file = 'ratings.json' 

 with open(ratings_file, 'r') as f: 
        data = json.loads(f.read()) 

查找与输入参数指定的用户相似的前三个用户。 您可以根据自己的选择将其更改为任意数量的用户。 打印输出和分数：

 print('\nUsers similar to ' + user + ':\n')
    similar_users = find_similar_users(data, user, 3) 
    print('User\t\t\tSimilarity score')
    print('-'*41)
    for item in similar_users:
        print(item[0], '\t\t', round(float(item[1]), 2)) 

完整代码在文件collaborative_filtering.py中给出。 让我们运行代码，找到像 Bill Duffy 这样的用户：

$ python3 collaborative_filtering.py --user "Bill Duffy" 

您将获得以下输出：

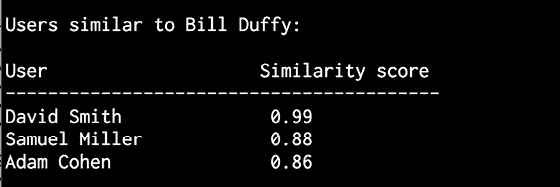
图 8：用户相似度输出

让我们运行代码，找到像 Clarissa Jackson 这样的用户：

$ python3 collaborative_filtering.py --user "Clarissa Jackson" 

您将获得以下输出：

图 9：用户相似度输出

在本节中，我们学习了如何在数据集中找到彼此相似的用户，以及如何分配分数来确定用户与另一个用户的相似程度。 在下一节中，我们将把它们放在一起并构建我们的推荐系统。

建立电影推荐系统

到目前为止，我们通过了解以下内容为构建推荐系统奠定了基础：

• 提取最近邻
• 建立 K 近邻分类器
• 计算相似度分数
• 使用协同过滤查找相似用户

现在所有的构建块都已就绪，现在该构建电影推荐系统了。 我们学习了构建推荐系统所需的所有基本概念。 在本节中，我们将基于文件ratings.json中提供的数据构建电影推荐系统。 此文件包含一组人物及其对各种电影的评分。 要查找给定用户的电影推荐，我们需要在数据集中找到相似的用户，然后提出针对此人的推荐。 让我们开始吧。

创建一个新的 Python 文件并导入以下包：

import argparse
import json
import numpy as np 

from compute_scores import pearson_score
from collaborative_filtering import find_similar_users 

定义一个函数来解析输入参数。 输入参数是用户的名称：

def build_arg_parser():
    parser = argparse.ArgumentParser(description='Find recommendations for the given user')
    parser.add_argument('--user', dest='user', required=True, 
            help='Input user')
    return parser 

定义一个函数以获取给定用户的电影推荐。 如果数据集中不存在该用户，则代码将引发错误：

# Get movie recommendations for the input user
def get_recommendations(dataset, input_user):
    if input_user not in dataset:
        raise TypeError('Cannot find ' + input_user + ' in the dataset') 

定义变量以跟踪分数：

 overall_scores = {}
    similarity_scores = {} 

计算输入用户与数据集中所有其他用户之间的相似性得分：

 for user in [x for x in dataset if x != input_user]: 
        similarity_score = pearson_score(dataset, input_user, user) 

如果相似度得分小于0，则可以继续使用数据集中的下一个用户：

 if similarity_score <= 0:
            continue 

提取当前用户已评级但输入用户未评级的电影列表：

 filtered_list = [x for x in dataset[user] if x not in \ 
                dataset[input_user] or dataset[input_user][x] == 0] 

对于过滤列表中的每个项目，请根据相似性分数跟踪加权等级。 同时跟踪相似度分数：

 for item in filtered_list:
            overall_scores.update({item: dataset[user][item] * similarity_score})
            similarity_scores.update({item: similarity_score}) 

如果没有这样的电影，那么我们将不推荐任何东西：

 if len(overall_scores) == 0:
        return ['No recommendations possible'] 

根据加权分数归一化分数：

 # Generate movie ranks by normalization
    movie_scores = np.array([[score/similarity_scores[item], item] 
            for item, score in overall_scores.items()]) 

排序分数并提取电影推荐：

 # Sort in decreasing order
    movie_scores = movie_scores[np.argsort(movie_scores[:, 0])[::-1]] 

 # Extract the movie recommendations
    movie_recommendations = [movie for _, movie in movie_scores] 

 return movie_recommendations 

定义main函数并解析输入参数以提取输入用户的名称：

if __name__=='__main__':
    args = build_arg_parser().parse_args()
    user = args.user 

从文件ratings.json加载电影收视率数据：

 ratings_file = 'ratings.json' 

 with open(ratings_file, 'r') as f: 
        data = json.loads(f.read()) 

提取电影推荐并打印输出：

 print("\nMovie recommendations for " + user + ":")
    movies = get_recommendations(data, user) 
    for i, movie in enumerate(movies):
        print(str(i+1) + '. ' + movie) 

完整代码在文件movie_recommender.py中给出。 让我们找到Chris Duncan的电影推荐：

$ python3 movie_recommender.py --user "Chris Duncan" 

您将看到以下输出：

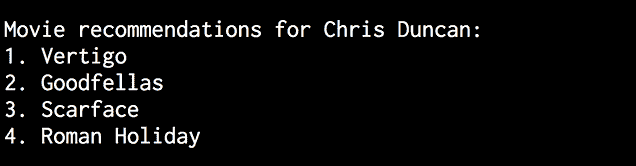
图 10：电影推荐

让我们找到Julie Hammel的电影推荐：

$ python3 movie_recommender.py --user "Julie Hammel" 

您将看到以下输出：

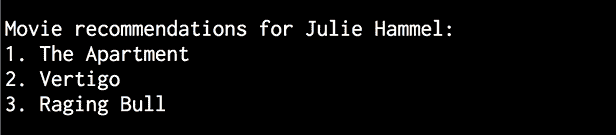
图 11：电影推荐

输出中的电影是系统的实际建议，基于先前对 Julie Hammel 观察到的偏好。 潜在地，仅通过观察更多和个数据点，系统就可以继续变得更好。

总结

在本章中，我们学习了如何从给定数据集中提取给定数据点的 K 最近邻。 然后，我们使用此概念来构建 K 最近邻分类器。 我们在中使用了如何计算相似度分数，例如欧几里得分数和皮尔逊分数。 我们学习了如何使用协同过滤从给定的数据集中查找相似的用户，并使用它来构建电影推荐系统。 最后，我们能够测试我们的模型并针对系统以前未见过的数据点运行它。

在下一章中，我们将学习逻辑编程，并了解如何构建可以解决实际问题的推理引擎。

9 逻辑编程

在本章中，我们将学习如何使用逻辑编程编写程序。 我们将讨论各种编程范例，并查看如何使用逻辑编程构造程序。 我们将学习逻辑编程的组成部分，并了解如何解决这一领域的问题。 我们将实现 Python 程序来构建各种解决各种问题的求解器。

在本章结束时，您将了解以下内容：

• 什么是逻辑编程？
• 了解逻辑编程的基础
• 使用逻辑编程解决问题
• 安装 Python 包
• 匹配数学表达式
• 验证素数
• 解析家谱
• 分析地理
• 构建一个解谜器

什么是逻辑编程？

逻辑编程是一种编程范例，基本上意味着它是一种进行编程的方法。 在我们讨论它的构成及其在人工智能（AI）中的相关性之前，让我们先讨论一下编程范例。

编程范例的概念源于对编程语言进行分类的需求。 它是指计算机程序通过代码解决问题的方式。

一些编程范例主要涉及含义或用于实现特定结果的操作顺序。 其他编程范例也关注我们如何组织代码。

以下是一些较流行的编程范例：

• 命令式：使用语句更改程序的状态，从而产生副作用。
• 函数式：将计算视为对数学函数的评估，并且不允许更改状态或可变数据。
• 声明式：一种编程的方式，其中，通过描述需要完成的操作而不是如何执行来编写程序。 在不明确描述控制流程的情况下表达了底层计算的逻辑。
• 面向对象：将程序中的代码分组，以使每个对象都对自己负责。 对象包含指定更改如何发生的数据和方法。
• 过程式：将代码分组为函数，每个函数负责一系列步骤。
• 符号式：使用样式的语法和语法，程序可通过将样式视为纯数据来修改其自身的组件。
• 逻辑式：将计算视为对由事实和规则组成的知识数据库的自动推理。

逻辑编程已经存在了一段时间。 在 AI 的最后一个鼎盛时期非常流行的语言是 Prolog。 它是仅使用三种构造的语言：

• 事实
• 规则
• 问题

但是使用这三种构造，您就可以构建一些强大的系统。 一种流行的用法是构建“专家系统”。 背后的想法是采访在特定领域工作了很长时间的人类专家，并将访谈编入 AI 系统。 构建专家系统的领域示例如下：

• 医学：著名的例子包括 MYCIN，INTERNIST-I 和 CADUCEUS
• 化学分析：DENDRAL 是用于预测分子结构的分析系统
• 财务：协助银行家贷款的咨询计划
• 调试程序：SAINT，MATLAB 和 MACSYMA

为了理解逻辑编程，有必要了解计算和演绎的概念。 为了计算某些东西，我们从一个表达式和一组规则开始。 这套规则基本上是程序。

表达式和规则用于生成输出。 例如，假设我们要计算 23、12 和 49 的总和：

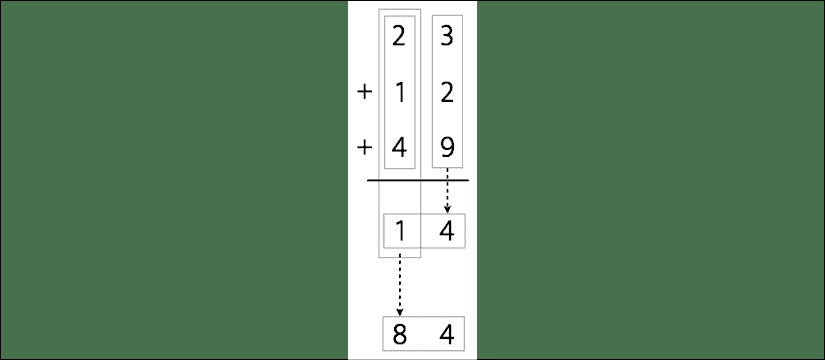
图 1：加法运算机制

完成操作的过程如下：

1. 相加3 + 2 + 9 = 14
2. 我们需要保留一个数字，即 4，然后携带 1
3. 相加2 + 1 + 4 + 1 = 8（加上我们携带的 1）
4. 结合 8 和 4。最终结果是：84

另一方面，要推断出某些东西，我们需要从一个推测开始。 证明是根据一组规则构造的。 计算过程是机械的，而演绎过程则更具创造性。

使用逻辑编程范例编写程序时，将基于有关问题域的事实和规则指定一组语句，然后求解器使用此信息进行求解。

了解逻辑编程的组成部分

在面向对象的或命令式编程中，始终需要定义一个变量。 在逻辑编程中，工作原理有所不同。 可以将未实例化的参数传递给函数，并且解释器将通过查看用户定义的事实来实例化这些变量。 这是解决变量匹配问题的有效方法。 将变量与不同项目进行匹配的过程称为统一。 这是逻辑编程不同的方式之一。 关系也可以在逻辑编程中指定。 关系通过称为事实和规则的子句来定义。

事实只是陈述，是关于程序和数据的真实情况。 语法很简单。 例如，“唐纳德是艾伦的儿子”是事实，而“艾伦的儿子是谁？”并非事实。 每个逻辑程序都需要事实，以便可以基于事实来实现给定的目标。

规则是我们在表达各种事实以及如何查询它们方面学到的知识。 它们是必须满足的约束，它们使您能够得出有关问题域的结论。 例如，假设您正在构建国际象棋引擎。 您需要指定有关如何在棋盘上移动的所有规则。

使用逻辑编程解决问题

逻辑编程使用事实和规则寻找解决方案。 必须为每个程序指定一个目标。 当逻辑程序和目标不包含任何变量时，求解器会提供一棵树，该树构成了用于解决问题和达到目标的搜索空间。

关于逻辑编程，最重要的事情之一就是我们如何对待规则。 规则可以视为逻辑语句。 让我们考虑以下内容：

Kathy orders dessert => Kathy is happy

这可以理解为：“如果 Kathy 很开心”和“则 Kathy 订购甜品”。 当凯西开心时，也可以将其解释为订购甜品。

同样，让我们​​考虑以下规则和事实：

canfly(X) :- bird(X), not abnormal(X).

abnormal(X) :- wounded(X).

bird(john).

bird(mary).

wounded(john).

以下是解释规则和事实的方法：

• 约翰受伤了
• 玛丽是鸟
• 约翰是鸟
• 受伤的鸟是异常的
• 没有异常的鸟可以飞

由此，我们可以得出结论，玛丽可以飞翔，而约翰不能飞翔。

在整个逻辑编程中，此结构以各种形式使用，以解决各种类型的问题。 让我们继续前进，看看如何解决 Python 中的这些问题。

安装 Python 包

在开始使用 Python 进行逻辑编程之前，我们需要安装几个包。 包logpy是一个 Python 包，可在 Python 中进行逻辑编程。 我们还将针对某些问题使用 SymPy。 因此，我们继续使用pip安装logpy和sympy：

$ pip3 install logpy
$ pip3 install sympy 

如果在logpy的安装过程中出现错误，则可以从这个页面的源代码安装它。 一旦成功安装了这些包，就可以继续进行下一部分的。

匹配数学表达式

我们一直遇到数学运算。 逻辑编程是比较表达式并找出未知值的有效方法。 让我们看看如何做到这一点。

创建一个新的 Python 文件并导入以下包：

from logpy import run, var, fact
import logpy.assoccomm as la 

定义几个数学运算：

# Define mathematical operations
add = 'addition'
mul = 'multiplication' 

加法和乘法都是交换操作（意味着可以对操作数进行翻转而不会改变结果）。 让我们指定：

# Declare that these operations are commutative 
# using the facts system
fact(la.commutative, mul)
fact(la.commutative, add)
fact(la.associative, mul)
fact(la.associative, add) 

让我们定义一些变量：

# Define some variables
a, b, c = var('a'), var('b'), var('c') 

考虑以下表达式：

expression_orig = 3 x (-2) + (1 + 2 x 3) x (-1) 

让我们用带掩码的变量生成该表达式。 第一个表达式是：

expression1 = (1 + 2 x a) x b + 3 x c

第二个表达式是：

expression2 = c x 3 + b x (2 x a + 1)

第三个表达式是：

expression3 = ((((2 x a) x b) + b) + 3 x c

如果仔细观察，所有三个表达式都代表相同的基本表达式。 目标是将这些表达式与原始表达式匹配以提取未知值：

# Generate expressions
expression_orig = (add, (mul, 3, -2), (mul, (add, 1, (mul, 2, 3)), -1))
expression1 = (add, (mul, (add, 1, (mul, 2, a)), b), (mul, 3, c))
expression2 = (add, (mul, c, 3), (mul, b, (add, (mul, 2, a), 1)))
expression3 = (add, (add, (mul, (mul, 2, a), b), b), (mul, 3, c)) 

将表达式与原始表达式进行比较。 方法运行通常在logpy中使用。 此方法采用输入参数并运行表达式。 第一个参数是值的数量，第二个参数是变量，第三个参数是函数：

# Compare expressions
print(run(0, (a, b, c), la.eq_assoccomm(expression1, expression_orig)))
print(run(0, (a, b, c), la.eq_assoccomm(expression2, expression_orig)))
print(run(0, (a, b, c), la.eq_assoccomm(expression3, expression_orig))) 

完整代码在expression_matcher.py中给出。 如果运行代码，将看到以下输出：

((3, -1, -2),)
((3, -1, -2),) 
() 

的前两行中的三个值表示a，b和c的值。 前两个表达式与原始表达式匹配，而第三个则什么也不返回。 这是因为，尽管第三个表达式在数学上是相同的，但在结构上却有所不同。 模式比较通过比较和表达式的结构来进行。

验证素数

让我们看看如何使用逻辑编程检查素数。 我们将使用logpy中可用的构造来确定给定列表中的哪些数字是质数，以及找出给定数字是否为质数。

创建一个新的 Python 文件并导入以下包：

import itertools as it
import logpy.core as lc
from sympy.ntheory.generate import prime, isprime 

接下来，定义一个函数，该函数根据数据类型检查给定数字是否为质数。 如果是数字，则很简单。 如果它是一个变量，那么我们必须运行顺序操作。 为了提供一些背景知识，方法conde是一个目标构造器，提供逻辑 AND 和 OR 运算。

方法condeseq类似于conde，但是它支持目标的通用迭代：

# Check if the elements of x are prime 
def check_prime(x):
    if lc.isvar(x):
        return lc.condeseq([(lc.eq, x, p)] for p in map(prime, it.count(1)))
    else:
        return lc.success if isprime(x) else lc.fail 

声明将要使用的变量x：

# Declate the variable 
x = lc.var() 

定义一组数字并检查哪些数字是质数。 方法membero 检查给定数字是否为输入参数中指定的数字列表的成员：

# Check if an element in the list is a prime number 
list_nums = (23, 4, 27, 17, 13, 10, 21, 29, 3, 32, 11, 19)
print('\nList of primes in the list:')
print(set(lc.run(0, x, (lc.membero, x, list_nums), (check_prime, x)))) 

现在，通过打印前 7 个质数，以稍微不同的方式使用该函数：

# Print first 7 prime numbers 
print('\nList of first 7 prime numbers:') 
print(lc.run(7, x, check_prime(x))) 

完整代码为prime.py中提供的。 如果运行代码，将看到以下输出：

List of primes in the list:
{3, 11, 13, 17, 19, 23, 29}
List of first 7 prime numbers: (2, 3, 5, 7, 11, 13, 17) 

您可以确认输出值正确。

解析族谱

现在，我们对逻辑编程有了更多的了解，让我们使用它来解决一个有趣的问题。 考虑以下族谱：

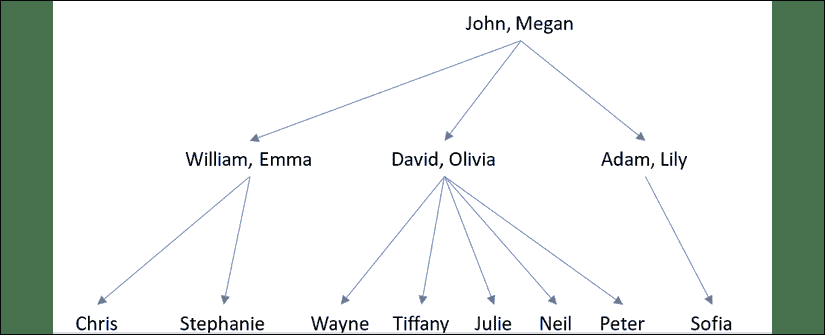
图 2：样本族谱

约翰和梅根有三个儿子-威廉，大卫和亚当。 威廉，大卫和亚当的妻子分别是艾玛，奥利维亚和莉莉。 威廉和艾玛有两个孩子-克里斯和斯蒂芬妮。 大卫和奥利维亚有五个孩子-韦恩，蒂芙尼，朱莉，尼尔和彼得。 亚当和莉莉有一个孩子-索菲娅。 基于这些事实，我们可以创建一个程序来告诉我们韦恩的祖父或索菲娅的叔叔的名字。 即使我们没有明确指定有关祖父母或叔叔关系的任何内容，逻辑编程也可以推断出它们。

这些关系是在为您提供的名为relationships.json的文件中指定的。 该文件如下所示：

{
       "father":
      [
              {"John": "William"},
              {"John": "David"},
              {"John": "Adam"},
              {"William": "Chris"},
              {"William": "Stephanie"},
              {"David": "Wayne"},
              {"David": "Tiffany"},
              {"David": "Julie"},
              {"David": "Neil"},
              {"David": "Peter"},
              {"Adam": "Sophia"}
      ],
      "mother":
      [
              {"Megan": "William"},
              {"Megan": "David"},
              {"Megan": "Adam"},
              {"Emma": "Stephanie"},
              {"Emma": "Chris"},
              {"Olivia": "Tiffany"},
              {"Olivia": "Julie"},
              {"Olivia": "Neil"},
              {"Olivia": "Peter"},
              {"Lily": "Sophia"}
    ]
} 

这是一个简单的 JSON 文件，用于指定父母之间的关系。 请注意，我们没有指定有关丈夫和妻子，祖父母或叔叔的任何信息。

创建一个新的 Python 文件并导入以下包：

import json
from logpy import Relation, facts, run, conde, var, eq 

定义一个函数来检查x是否是y的父级。 我们将使用以下逻辑：如果x是y的父母，则x是父亲或母亲。 我们已经在事实基础中定义了“父亲”和“母亲”：

# Check if 'x' is the parent of 'y' 
def parent(x, y):
    return conde([father(x, y)], [mother(x, y)]) 

定义一个函数来检查x是否为y的祖父母。 我们将使用以下逻辑：如果x是y的祖父母，则x的后代将是y的父代：

# Check if 'x' is the grandparent of 'y' 
def grandparent(x, y):
    temp = var()
    return conde((parent(x, temp), parent(temp, y))) 

定义一个函数来检查x是否是y的兄弟。 我们将使用以下逻辑：如果x是y的兄弟，则x和y将具有相同的父代。 请注意，此处需要进行一些修改，因为当我们列出x的所有同级时，也会列出x，因为x满足这些条件。 因此，当我们打印输出时，我们将不得不从列表中删除x。 我们将在main函数中对此进行讨论：

# Check for sibling relationship between 'a' and 'b' 
def sibling(x, y):
    temp = var()
    return conde((parent(temp, x), parent(temp, y))) 

定义一个函数以检查x是否是y的叔叔。 我们将使用以下逻辑：如果x是y的叔叔，那么x的祖父母将与y的父母相同。 请注意，此处需要进行一些修改，因为当我们列出x的所有叔叔时，也会列出x的父亲，因为x的父亲满足了这些条件。 因此，当我们打印输出时，我们将不得不从列表中删除x的父亲。 我们将在main函数中对此进行讨论：

# Check if x is y's uncle 
def uncle(x, y):
    temp = var()
    return conde((father(temp, x), grandparent(temp, y))) 

定义main函数并初始化关系father和mother：

if __name__=='__main__':
    father = Relation()
    mother = Relation() 

从relationships.json文件中加载数据：

 with open('relationships.json') as f: 
        d = json.loads(f.read()) 

读取数据并将其添加到事实库：

 for item in d['father']:
        facts(father, (list(item.keys())[0], list(item.values())[0])) 

 for item in d['mother']:
        facts(mother, (list(item.keys())[0], list(item.values())[0])) 

定义变量x：

 x = var() 

现在，我们准备提出一些问题，看看求解器能否提出正确的答案。 让我们问一下约翰的孩子是谁：

 # John's children 
    name = 'John'
    output = run(0, x, father(name, x)) 
    print("\nList of " + name + "'s children:") 
    for item in output:
        print(item) 

威廉的母亲是谁？

 # William's mother 
    name = 'William'
    output = run(0, x, mother(x, name))[0] 
    print("\n" + name + "'s mother:\n" + output) 

亚当的父母是谁？

 # Adam's parents name = 'Adam'
    output = run(0, x, parent(x, name)) 
    print("\nList of " + name + "'s parents:") 
    for item in output:
        print(item) 

谁是韦恩的祖父母？

 # Wayne's grandparents name = 'Wayne'
    output = run(0, x, grandparent(x, name)) 
    print("\nList of " + name + "'s grandparents:") 
    for item in output:
        print(item) 

梅根的孙子是谁？

 # Megan's grandchildren
    name = 'Megan'
    output = run(0, x, grandparent(name, x)) 
    print("\nList of " + name + "'s grandchildren:") 
    for item in output:
        print(item) 

大卫的兄弟姐妹是谁？

 # David's siblings
    name = 'David'
    output = run(0, x, sibling(x, name)) 
    siblings = [x for x in output if x != name] 
    print("\nList of " + name + "'s siblings:") 
    for item in siblings:
        print(item) 

蒂芙尼的叔叔是谁

 # Tiffany's uncles
    name = 'Tiffany'
    name_father = run(0, x, father(x, name))[0] 
    output = run(0, x, uncle(x, name))
    output = [x for x in output if x != name_father] 
    print("\nList of " + name + "'s uncles:")
    for item in output: 
        print(item) 

列出家庭中的所有配偶：

 # All spouses
    a, b, c = var(), var(), var()
    output = run(0, (a, b), (father, a, c), (mother, b, c)) 
    print("\nList of all spouses:")
    for item in output:
        print('Husband:', item[0], '<==> Wife:', item[1]) 

完整代码为family.py中提供的。 如果运行代码，您将看到一些输出。 前半部分如下所示：

图 3：族谱示例输出

下半部分如下所示：：

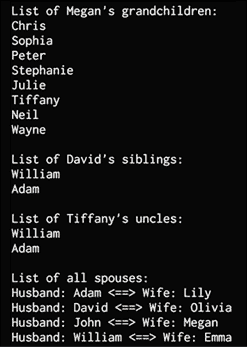
图 4：族谱示例输出

您可以将输出与族谱进行比较，以确保在位上的确实正确。

地理分析

让我们使用逻辑编程来建立一个求解器来分析地理。 在此问题中，我们将指定有关美国各州位置的信息，然后查询程序以根据这些事实和规则回答各种问题。 以下是美国的地图：

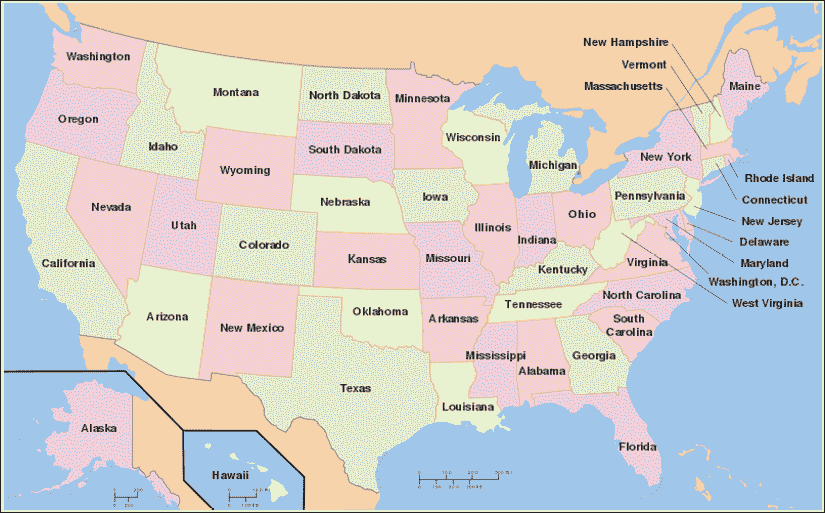
图 5：相邻和沿海州示例图

已为您提供了两个名为adjacent_states.txt 和coastal_states.txt的文本文件。 这些文件包含有关哪些州彼此相邻以及哪些州沿岸的详细信息。 基于此，我们可以获得有趣的信息，例如“俄克拉荷马州和德克萨斯州都毗邻哪些州？” 或“哪个沿海州与新墨西哥州和路易斯安那州相邻？”

创建一个新的 Python 文件并导入以下内容：

from logpy import run, fact, eq, Relation, var 

初始化关系：

adjacent = Relation()
coastal = Relation() 

定义输入文件以从以下位置加载数据：

file_coastal = 'coastal_states.txt' 
file_adjacent = 'adjacent_states.txt' 

加载数据：

# Read the file containing the coastal states
with open(file_coastal, 'r') as f:
    line = f.read()
    coastal_states = line.split(',') 

将信息添加到事实库：

# Add the info to the fact base 
for state in coastal_states:
    fact(coastal, state) 

读取相邻数据：

# Read the file containing the coastal states 
with open(file_adjacent, 'r') as f:
    adjlist = [line.strip().split(',') for line in f if line and line[0].isalpha()] 

将邻接信息添加到事实库中：

# Add the info to the fact base 
for L in adjlist:
    head, tail = L[0], L[1:]
    for state in tail:
        fact(adjacent, head, state) 

初始化变量x和y：

# Initialize the variables
x = var()
y = var() 

现在，我们准备提出一些问题。 检查内华达州是否与路易斯安那州相邻：

# Is Nevada adjacent to Louisiana?
output = run(0, x, adjacent('Nevada', 'Louisiana')) 
print('\nIs Nevada adjacent to Louisiana?:') 
print('Yes' if len(output) else 'No') 

打印出与俄勒冈州相邻的所有州：

# States adjacent to Oregon
output = run(0, x, adjacent('Oregon', x)) 
print('\nList of states adjacent to Oregon:') 
for item in output:
    print(item) 

列出与密西西比州相邻的所有沿海州：

# States adjacent to Mississippi that are coastal
output = run(0, x, adjacent('Mississippi', x), coastal(x)) 
print('\nList of coastal states adjacent to Mississippi:') 
for item in output:
    print(item) 

列出与沿海国接壤的七个州：

# List of 'n' states that border a coastal state n = 7
output = run(n, x, coastal(y), adjacent(x, y))
print('\nList of ' + str(n) + ' states that border a coastal state:') 
for item in output:
    print(item) 

列出与阿肯色州和肯塔基州相邻的州：

# List of states that adjacent to the two given states
output = run(0, x, adjacent('Arkansas', x), adjacent('Kentucky', x)) 
print('\nList of states that are adjacent to Arkansas and Kentucky:') 
for item in output:
    print(item) 

完整代码在states.py中给出。 如果运行代码，将看到以下输出：

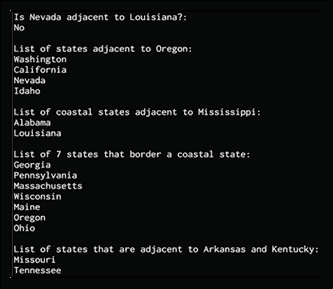
图 6：相邻和沿海州示例输出

您可以将输出与美国地图进行交叉检查，以验证答案是否正确。 您也可以在程序中添加更多问题，以查看是否可以回答这些问题。

构建难题解决器

逻辑编程的另一个有趣的应用是解决难题。 我们可以指定难题的条件，程序将提供解决方案。 在本节中，我们将指定有关四个人的各种信息，并要求提供丢失的信息。

在逻辑程序中，我们按如下方式指定难题：

• 史蒂夫有辆蓝色的汽车。
• 养猫的人住在加拿大。 马修住在美国。
• 拥有黑色汽车的人居住在澳大利亚。
• 杰克有一只猫。
• 阿尔弗雷德（Alfred）居住在澳大利亚。
• 养狗的人住在法国。
• 谁有兔子？

目的是找到有兔子的人。 以下是有关这四个人的完整详细信息：

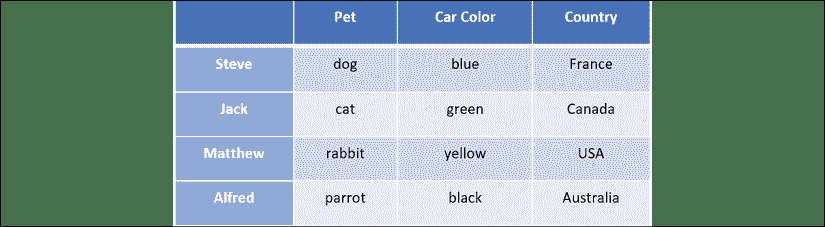
图 7：解谜器输入数据

创建一个新的 Python 文件并导入以下包：

from logpy import *
from logpy.core import lall 

声明变量people：

# Declare the variable people
people = var() 

使用lall定义所有规则。 第一条规则是有四个人：

# Define the rules
rules = lall(
    # There are 4 people
    (eq, (var(), var(), var(), var()), people), 

名为史蒂夫的人有一辆蓝色轿车：

 # Steve's car is blue
    (membero, ('Steve', var(), 'blue', var()), people), 

养猫的人住在加拿大：

 # Person who has a cat lives in Canada
    (membero, (var(), 'cat', var(), 'Canada'), people), 

名为 Matthew 的人住在美国：

 # Matthew lives in USA
    (membero, ('Matthew', var(), var(), 'USA'), people), 

拥有黑色汽车的人居住在澳大利亚：

 # The person who has a black car lives in Australia 
    (membero, (var(), var(), 'black', 'Australia'), people), 

叫杰克的人有一只猫：

 # Jack has a cat
    (membero, ('Jack', 'cat', var(), var()), people), 

名为 Alfred 的人居住在澳大利亚：

 # Alfred lives in Australia
    (membero, ('Alfred', var(), var(), 'Australia'), people), 

养狗的人住在法国：

 # Person who owns the dog lives in France
    (membero, (var(), 'dog', var(), 'France'), people), 

这一组人中有一只兔子。 那个人是谁？

 # Who has a rabbit?
    (membero, (var(), 'rabbit', var(), var()), people)
) 

使用上述约束运行求解器：

# Run the solver
solutions = run(0, people, rules) 

从解决方案中提取输出：

# Extract the output
output = [house for house in solutions[0] if 'rabbit' in house][0][0] 

打印从求解器获得的完整矩阵：

# Print the output
print('\n' + output + ' is the owner of the rabbit') 
print('\nHere are all the details:')
attribs = ['Name', 'Pet', 'Color', 'Country'] 
print('\n' + '\t\t'.join(attribs))
print('=' * 57)
for item in solutions[0]:
    print('')
    print('\t\t'.join([str(x) for x in item])) 

完整代码在puzzle.py中给出。 如果运行代码，将看到以下输出：

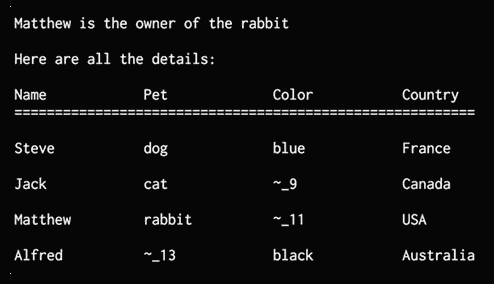
图 8：解谜器输出

前面的图显示了使用求解器获得的所有值。 如编号名称所示，其中一些仍然未知。 即使信息不完整，求解器仍能够回答问题。 但是为了回答每个问题，您可能需要添加更多规则。 该程序旨在演示如何用不完整的信息解决难题。 您可以尝试使用它，看看如何为各种场景构建拼图解算器。

总结

在本章中，我们学习了如何使用逻辑编程编写 Python 程序。 我们讨论了各种编程范例如何处理构建程序。 我们了解了如何在逻辑编程中构建程序。 我们了解了逻辑编程的各种构建块，并讨论了如何解决此领域的问题。 我们实现了各种 Python 程序来解决有趣的问题和难题。

在下一章中，我们将学习启发式搜索技术，并使用这些算法来解决现实世界中的问题。

10 启发式搜索技术

在本章中，我们将学习启发式搜索技术。 启发式搜索技术用于搜索解决方案空间以得出答案。 使用指导搜索算法的试探法进行搜索。 这种启发式算法可使算法加快处理速度，否则将需要很长时间才能得出解决方案。

在本章结束时，您将了解以下内容：

• 什么是启发式搜索？
• 不知情还是知情搜索
• 约束满意度问题
• 本地搜索技术
• 模拟退火
• 使用贪婪搜索构造字符串
• 解决约束问题
• 解决区域着色问题
• 构建 8 难题求解器
• 构建一个迷宫求解器

启发式搜索是人工智能吗？

在第 2 章，“人工智能的基本用例”中，我们了解了 Pedro Domingos 定义的五个流派。 符号主义者流派是最“古老”的流派之一。 至少对我来说，这一事实不足为奇。 作为人类，我们尝试在所有事物中找到规则和模式。 不幸的是，世界有时是混乱的，并非所有事物都遵循简单的规则。

这就是为什么当我们没有秩序的世界时，其他流派出现来帮助我们的原因。 但是，当我们的搜索空间较小且域受到限制时，使用启发式，约束满足以及本章中介绍的其他技术对于这组问题很有用。 当组合的数量相对较少且组合爆炸受到限制时，这些技术很有用。 例如，当城市数量大约为 20 时，使用这些技术解决旅行商问题很简单。如果我们尝试对n = 2000求解相同的问题，则必须使用其他方法来解决。 不要探索整个空间，而只能给出结果的近似值。

什么是启发式搜索？

搜索和组织数据是人工智能中的重要主题。 有许多问题需要在解决方案领域内寻找答案。 对于给定的问题，有许多可能的解决方案，我们不知道哪个是正确的。 通过有效地组织数据，我们可以快速有效地寻找解决方案。

通常，解决给定问题的选项太多，以至于无法开发单个算法来找到确定的最佳解决方案。 同样，不可能通过所有解决方案，因为这过于昂贵。 在这种情况下，我们依靠经验法则，通过消除明显错误的选项来帮助我们缩小搜索范围。 这个经验法则称为，称为启发式。 使用启发式搜索指导搜索的方法称为启发式搜索。

启发式技术之所以强大，是因为它们可以加快过程。 即使启发式方法无法消除某些选项，也将有助于排序选项，以便可能首先提出更好的解决方案。 如前所述，启发式搜索在计算上可能会很昂贵。 现在，我们将学习如何使用快捷方式和修剪搜索树。

不知情或知情的搜索

如果您熟悉计算机科学，则可能听说过深度优先搜索（DFS），广度优先搜索（BFS），以及统一成本搜索（UCS）。 这些是搜索技术，其中通常用于图形上以获得解决方案。 这些是不知情的搜索示例。 他们不使用任何先验信息或规则来消除某些路径。 他们检查所有可能的路径并选择最佳路径。

另一方面，启发式搜索称为通知搜索，因为它使用先验信息或规则来消除不必要的路径。 不了解情况的搜索技术不会考虑目标。 不了解情况的搜索技术会盲目搜索，并且对最终解决方案没有先验知识。

在图问题中，启发式可以用来指导搜索。 例如，在每个节点处，我们可以定义一个启发式函数，该函数返回一个分数，该分数表示从当前节点到目标的路径成本估计。 通过定义此启发式函数，我们可以将正确的方向告知搜索技术以达到目标。 这将允许算法识别哪个邻居将导致目标。

我们需要注意，启发式搜索可能并不总是总是找到最佳解决方案。 这是因为我们不是在探索每种可能性，而是在依靠启发式方法。 搜索可以确保在合理的时间内找到一个好的解决方案，但这是我们对实际解决方案的期望。 在现实世界中，我们需要快速有效的解决方案。 启发式搜索通过快速找到合理的解决方案来提供有效的解决方案。 它们用于无法以其他任何方式解决问题或需要很长时间才能解决的问题。 修剪树的另一种方法是利用数据固有的约束。 在下一部分中，我们将学习更多利用这些约束的修剪技术。

约束满意度问题

有许多必须在约束条件下解决的问题。 这些约束基本上是解决问题的过程中不能违反的条件。

这些问题称为约束满意度问题（CSP）。

为了获得一些直观的理解，让我们快速看一下数独拼图的示例部分。 数独游戏是我们不能在水平线，垂直线或同一方块中两次拥有相同的数字。 这是数独板的示例：

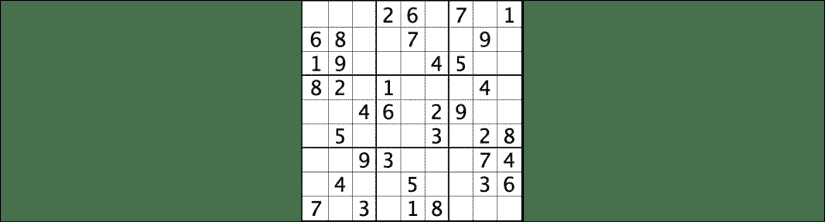
图 1：数独板的示例

使用约束的满意度和数独的规则，我们可以快速确定尝试使用哪些数字以及不尝试解决该难题的数字。 例如，在这个方块中：

图 2：考虑数独问题

如果我们不使用 CSP，则一种暴力方法是尝试插槽中所有数字的组合，然后检查规则是否适用。 例如，我们的第一个尝试可能是用数字 1 填充所有正方形，然后检查结果。

使用 CSP，我们可以在尝试之前对它们进行修剪。

让我们来看看我们认为数字应该是红色突出显示的正方形的含义。 我们知道该数字不能为 1、6、8 或 9，因为这些数字已经存在于正方形中。 我们也知道它不能为 2 或 7，因为这些数字存在于水平线中。 我们也知道它不能是 3 或 4，因为这些数字已经在垂直线上。 这给我们留下了唯一的可能性，数字应该是 5。

CSP 是数学上的问题，定义为一组必须满足一些约束的变量。 当我们得出最终解决方案时，变量的状态必须服从所有约束。 该技术将涉及给定问题的实体表示为变量上固定数量的约束的集合。 这些变量需要通过约束满足方法来解决。

这些问题需要在合理的时间内解决启发式方法和其他搜索技术的问题。 在这种情况下，我们将使用约束满足技术来解决有限域上的问题。 有限域由有限数量的元素组成。 由于我们正在处理有限域，因此我们可以使用搜索技术来获得解决方案。 为了进一步了解 CSP，我们现在将学习如何使用本地搜索技术来解决 CSP 问题。

本地搜索技术

本地搜索是解决 CSP 的一种方法。 它会不断优化解决方案，直到满足所有约束条件为止。 迭代地不断更新变量，直到我们到达目的地。 这些算法会在过程的每个步骤中修改值，使我们更接近目标。 在解决方案空间中，更新的值比先前的值更接近目标。 因此，这被称为本地搜索。

局部搜索算法是一种启发式搜索算法。 这些算法使用一个函数来计算每次更新的质量。 例如，它可以计算当前更新违反的约束数量，也可以查看更新如何影响到目标的距离。 这称为分配成本。 本地搜索的总体目标是在每个步骤中找到最小的成本更新。

爬山是流行的本地搜索技术。 它使用一种启发式函数来衡量当前状态和目标之间的差异。 当我们开始时，它将检查状态是否是最终目标。 如果是，则停止。 如果不是，则选择更新并生成新状态。 如果它比当前状态更接近目标，那么它将成为当前状态。 如果不是，它将忽略它并继续该过程，直到检查所有可能的更新。 它基本上是爬山直到到达山顶。

图 3： 爬山

模拟退火

模拟退火是本地搜索的一种，也是一种随机搜索技术。 随机搜索技术广泛用于各种领域，例如机器人技术，化学，制造，医学和经济学。 随机算法用于解决许多现实问题：我们可以执行诸如优化机器人设计，确定工厂中自动控制的时序策略以及规划交通量之类的事情。

模拟退火是爬山技术的一种变化。 爬山的主要问题之一是，它最终会爬上错误的山麓小丘。 这意味着它被卡在局部最大值中。 因此，在做出任何攀登决定之前，最好先检查一下整个空间。 为了实现这一目标，首先对整个空间进行探索以了解其外观。 这有助于我们避免陷入高原或局部最大值。

在模拟退火中，我们重新构造了问题并针对最小化（而不是最大化）进行了求解。 因此，我们现在正下降到山谷中，而不是爬山。 我们几乎在做相同的事情，但是方式不同。

我们使用目标函数来指导搜索。 该目标函数用作试探法。

之所以将其称为模拟退火是因为它源自冶金过程。 在此过程中，我们首先加热金属，使原子扩散到金属中，然后冷却直到达到原子结构安排所需的最佳状态。 通常，这是为了改变金属的物理特性，使其变得更软，更容易加工。

我们冷却系统的速率称为，退火时间表。 冷却速度很重要，因为它会直接影响结果。 在金属的现实世界中，如果冷却速度过快，则最终会过快地陷入非理想状态（原子结构）。 例如，如果将加热的金属放入冷水中，它最终会很快沉降到不需要的结构中，从而使金属变脆。

如果冷却速度缓慢且可控，则金属就有机会达到最佳原子结构，从而获得所需的物理表现。 在这种情况下，迅速采取大步向任何山丘进发的机会较低。 由于冷却速度很慢，因此需要花费一些时间才能进入最佳状态。 可以用数据完成类似的操作。

我们首先评估当前的状态，看看它是否已达到目标。 如果有，那么我们停止。 如果不是，则将最佳状态变量设置为当前状态。 然后，我们定义一个退火计划，以控制其下降到谷底的速度。 计算当前状态和新状态之间的差异。 如果新状态不是更好，则以一定的预定义概率将其设置为当前状态。 这是使用随机数生成器并根据阈值确定的。 如果它高于阈值，那么我们将最佳状态设置为该状态。 基于此，根据节点数更新退火计划。 我们一直这样做，直到达到目标。 另一个本地搜索技术是贪婪搜索算法。 我们将在下一部分中详细了解。

使用贪婪搜索构造字符串

贪婪搜索是一种算法范式，它在每​​个阶段进行局部最优选择，以便找到全局最优值。 但是在许多问题中，贪婪算法无法产生全局最优解。 使用贪婪算法的一个优点是它们可以在合理的时间内产生一个近似解。 希望该近似解可以合理地接近全局最优解。

贪婪算法不会在搜索过程中基于新的信息来优化的解决方案。 例如，假设您正在计划一次公路旅行，并且想要采取最佳路线。 如果您使用贪婪算法来规划路线，则可能会要求您选择距离较短但可能会花费更多时间的路线。 在短期内，这也可能会导致您走上更快的路径，但稍后可能会导致交通拥堵。 发生这种情况是因为贪婪算法只看到下一步，而没有全局最优的最终解决方案。

让我们看看如何使用贪婪搜索解决问题。 在此问题中，我们将尝试根据字母重新创建输入字符串。 我们将要求算法搜索解决方案空间并构建解决方案的路径。

在本章中，我们将使用名为simpleai的包。 它包含各种例程，这些例程可用于使用启发式搜索技术构建解决方案。 可在这个页面上获得。 为了使它在 Python3 中工作，我们需要对源代码进行一些更改。随同本书的代码一起提供了一个名为simpleai.zip的文件。 将此文件解压缩到名为simpleai的文件夹中。 此文件夹包含对原始库的所有必要更改，以使其能够在 Python3 中工作。将simpleai文件夹与您的代码位于同一文件夹中，你将能够顺利运行你的代码。

创建一个新的 Python 文件并导入以下包：

import argparse
import simpleai.search as ss 

定义一个函数来解析输入参数：

def build_arg_parser():
    parser = argparse.ArgumentParser(description='Creates the input string \
            using the greedy algorithm')
    parser.add_argument("--input-string", dest="input_string", required=True,
            help="Input string")
    parser.add_argument("--initial-state", dest="initial_state", required=False,
            default='', help="Starting point for the search") 
    return parser 

创建一个包含解决问题所需方法的类。 此类继承了库中可用的SearchProblem类。 需要重写一些方法来解决当前的问题。 第一种方法set_target是定义目标字符串的自定义方法：

class CustomProblem(ss.SearchProblem):
    def set_target(self, target_string):
        self.target_string = target_string 

这些动作是SearchProblem随附的一种方法，需要重写。 它负责朝着目标采取正确的步骤。 如果当前字符串的长度小于目标字符串的长度，它将返回可能的字母列表以供选择。 如果没有，它将返回一个空字符串：

 # Check the current state and take the right action
    def actions(self, cur_state):
        if len(cur_state) < len(self.target_string):
            alphabets = 'abcdefghijklmnopqrstuvwxyz'
            return list(alphabets + ' ' + alphabets.upper())
        else:
            return [] 

现在创建一个方法，通过将当前字符串和需要采取的措施连接起来来计算结果。 此方法随附SearchProblem，我们将其覆盖：

 # Concatenate state and action to get the result
    def result(self, cur_state, action):
        return cur_state + action 

方法is_goal是SearchProblem的一部分，用于检查是否已达到目标：

 # Check if goal has been achieved 
    def is_goal(self, cur_state):
        return cur_state == self.target_string 

方法heuristic也是SearchProblem的一部分，我们需要重写它。 定义了一种启发式方法，即将用于解决该问题。 执行计算以查看目标有多远，并将其用作启发将其引导至目标：

 # Define the heuristic that will be used 
    def heuristic(self, cur_state):
        # Compare current string with target string 
        dist = sum([1 if cur_state[i] != self.target_string[i] else 0 
                    for i in range(len(cur_state))]) 

 # Difference between the lengths
        diff = len(self.target_string) - len(cur_state)
        return dist + diff 

初始化输入参数：

if __name__=='__main__':
    args = build_arg_parser().parse_args() 

初始化CustomProblem对象：

 # Initialize the object 
    problem = CustomProblem() 

设置起点和我们要实现的目标：

 # Set target string and initial state 
    problem.set_target(args.input_string) 
    problem.initial_state = args.initial_state 

运行求解器：

 # Solve the problem
    output = ss.greedy(problem) 

打印解决方案的路径：

 print('\nTarget string:', args.input_string) 
    print('\nPath to the solution:')
    for item in output.path(): 
        print(item) 

完整代码在文件greedy_search.py中给出。 如果您以空的初始状态运行代码：

$ python3 greedy_search.py --input-string 'Artificial Intelligence' --initial-state '' 

您将获得以下输出：

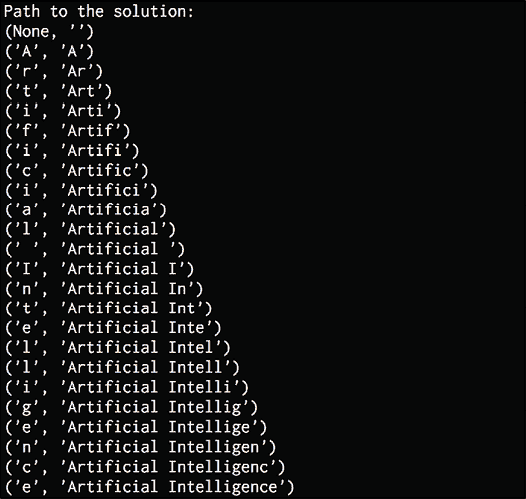
图 4：以空的初始状态运行时的代码输出

如果您以非空的起点运行代码：

$ python3 greedy_search.py --input-string 'Artificial Intelligence with Python' --initial-state 'Artificial Inte' 

您将获得以下输出：

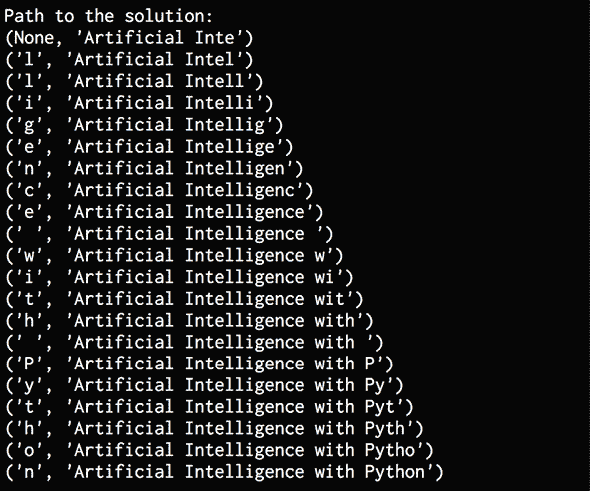
图 5：以非空初始状态运行时的代码输出

现在我们已经涵盖了一些流行的搜索技术，我们将继续使用这些搜索算法来解决一些实际问题。

解决带约束的问题

我们已经讨论了如何制定 CSP。 让我们将应用于实际问题。 在此问题中，我们有一个名称列表，每个名称可以采用一组固定的值。 这些人之间还存在一系列需要满足的约束。 让我们来看看如何做。

创建一个新的 Python 文件并导入以下包：

from simpleai.search import CspProblem, backtrack, \
        min_conflicts, MOST_CONSTRAINED_VARIABLE, \
        HIGHEST_DEGREE_VARIABLE, LEAST_CONSTRAINING_VALUE 

定义约束，该约束指定输入列表中的所有变量应具有唯一值：

# Constraint that expects all the different variables 
# to have different values
def constraint_unique(variables, values):
    # Check if all the values are unique
    return len(values) == len(set(values)) 

定义约束，该约束指定第一个变量应大于第二个变量：

# Constraint that specifies that one variable
# should be bigger than other
def constraint_bigger(variables, values):
    return values[0] > values[1] 

定义指定的约束，如果第一个变量为奇数，则第二个变量应为偶数，反之亦然：

# Constraint that specifies that there should be
# one odd and one even variables in the two variables
def constraint_odd_even(variables, values):
    # If first variable is even, then second should
    # be odd and vice versa
    if values[0] % 2 == 0:
        return values[1] % 2 == 1 
    else:
        return values[1] % 2 == 0 

定义main函数并定义变量：

if __name__=='__main__':
    variables = ('John', 'Anna', 'Tom', 'Patricia') 

定义每个变量可以采用的值列表：

 domains = {
        'John': [1, 2, 3],
        'Anna': [1, 3],
        'Tom': [2, 4],
        'Patricia': [2, 3, 4],
    } 

定义各种方案的约束。 在这种情况下，我们指定了以下三个约束：

• 约翰，安娜和汤姆应该有不同的值
• 汤姆的值应大于安娜的值
• 如果 John 的值是奇数，则 Patricia 的值应该是偶数，反之亦然

使用以下代码：

 constraints = [
        (('John', 'Anna', 'Tom'), constraint_unique),
        (('Tom', 'Anna'), constraint_bigger),
        (('John', 'Patricia'), constraint_odd_even),
    ] 

使用前面的变量和约束来初始化CspProblem对象：

 problem = CspProblem(variables, domains, constraints) 

计算解决方案并打印：

 print('\nSolutions:\n\nNormal:', backtrack(problem)) 

使用和MOST_CONSTRAINED_VARIABLE启发式计算解决方案：

 print('\nMost constrained variable:', backtrack(problem,
            variable_heuristic=MOST_CONSTRAINED_VARIABLE)) 

使用HIGHEST_DEGREE_VARIABLE启发式计算解决方案：

 print('\nHighest degree variable:', backtrack(problem, 
            variable_heuristic=HIGHEST_DEGREE_VARIABLE)) 

使用LEAST_CONSTRAINING_VALUE启发式计算解决方案：

 print('\nLeast constraining value:', backtrack(problem, 
            value_heuristic=LEAST_CONSTRAINING_VALUE)) 

使用MOST_CONSTRAINED_VARIABLE变量启发式和LEAST_CONSTRAINING_VALUE值启发式计算解决方案：

 print('\nMost constrained variable and least constraining value:',
            backtrack(problem, variable_heuristic=MOST_CONSTRAINED_VARIABLE, 
            value_heuristic=LEAST_CONSTRAINING_VALUE)) 

使用HIGHEST_DEGREE_VARIABLE变量启发式和LEAST_CONSTRAINING_VALUE值启发式计算解决方案：

 print('\nHighest degree and least constraining value:', 
            backtrack(problem, variable_heuristic=HIGHEST_DEGREE_VARIABLE, 
            value_heuristic=LEAST_CONSTRAINING_VALUE)) 

使用最小冲突启发式计算解决方案：

print('\nMinimum conflicts:', min_conflicts(problem)) 

完整代码为文件constrained_problem.py中提供的。 如果运行，则将得到以下输出：

图 6：以最小冲突启发式计算解决方案

您可以检查约束条件以查看解决方案是否满足所有这些约束条件。

解决区域着色问题

让我们使用约束满足框架来解决区域着色问题。 考虑以下屏幕截图：

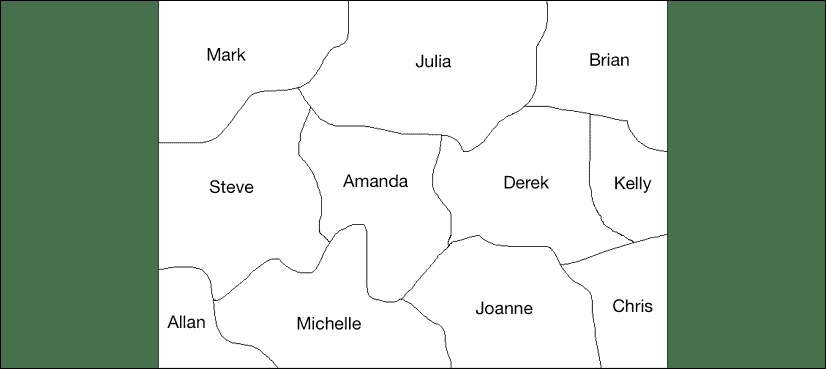
图 7：区域着色问题的框架

在上图中，我们有一些区域用名称标记。 目标是用四种颜色进行着色，以使相邻区域都不具有相同的颜色。

创建一个新的 Python 文件并导入以下包：

from simpleai.search import CspProblem, backtrack 

定义指定值应该不同的约束：

# Define the function that imposes the constraint 
# that neighbors should be different
def constraint_func(names, values):
    return values[0] != values[1] 

定义main函数并指定名称列表：

if __name__=='__main__':
    # Specify the variables
    names = ('Mark', 'Julia', 'Steve', 'Amanda', 'Brian',
            'Joanne', 'Derek', 'Allan', 'Michelle', 'Kelly') 

定义可能的颜色列表：

 # Define the possible colors
    colors = dict((name, ['red', 'green', 'blue', 'gray']) for name in names) 

我们需要将地图信息转换为该算法可以理解的信息。 让我们通过指定彼此相邻的人员列表来定义约束：

 # Define the constraints
    constraints = [
        (('Mark', 'Julia'), constraint_func),
        (('Mark', 'Steve'), constraint_func),
        (('Julia', 'Steve'), constraint_func),
        (('Julia', 'Amanda'), constraint_func),
        (('Julia', 'Derek'), constraint_func),
        (('Julia', 'Brian'), constraint_func),
        (('Steve', 'Amanda'), constraint_func),
        (('Steve', 'Allan'), constraint_func),
        (('Steve', 'Michelle'), constraint_func),
        (('Amanda', 'Michelle'), constraint_func),
        (('Amanda', 'Joanne'), constraint_func),
        (('Amanda', 'Derek'), constraint_func),
        (('Brian', 'Derek'), constraint_func),
        (('Brian', 'Kelly'), constraint_func),
        (('Joanne', 'Michelle'), constraint_func),
        (('Joanne', 'Amanda'), constraint_func),
        (('Joanne', 'Derek'), constraint_func),
        (('Joanne', 'Kelly'), constraint_func),
        (('Derek', 'Kelly'), constraint_func),
    ] 

使用变量和约束来初始化对象：

 # Solve the problem
    problem = CspProblem(names, colors, constraints) 

解决问题并打印解决方案：

 # Print the solution
    output = backtrack(problem) 
    print('\nColor mapping:\n') 
    for k, v in output.items():
        print(k, '==>', v) 

完整代码为文件coloring.py中提供的。 如果运行代码，将得到以下输出：

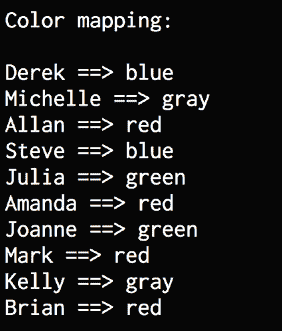
图 8：颜色映射输出

如果根据此输出为区域着色，将获得以下机翼：

图 9：解决区域着色问题

您可以检查没有两个相邻的区域具有相同的颜色。

构建 8 拼图求解器

8 拼图是 15 拼图的变体。 您可以在这个页面上进行检查。 您将看到一个随机的网格，目标是将其恢复为原始的有序配置。 您可以在这个页面上玩游戏以熟悉。

我们将使用A*算法解决此问题。 它是一种算法，用于在图中找到解决方案的路径。 该算法是 Dijkstra 算法和贪婪最佳优先搜索的组合。 A*算法不会盲目猜测下一步该怎么做，而是选择看起来最有前途的算法。 在每个节点上，生成所有可能性的列表，然后选择达到目标所需的最低成本的可能性。

让我们看看如何定义成本函数。 在每个节点上，都需要计算成本。 该成本基本上是两个成本的总和-第一个成本是到达当前节点的成本，第二个成本是从当前节点达到目标的成本。

我们将此求和用作启发式方法。 如我们所见，第二笔费用基本上是不理想的估计。 如果是完美的，那么A*算法将很快到达解决方案。 但这不是通常的情况。 找到解决方案的最佳路径需要花费一些时间。 A*有效地找到最佳路径，并且是其中最流行的技术之一。

让我们使用A*算法来构建 8 难题求解器。 这是simpleai库中提供的解决方案的变体。 创建一个新的 Python 文件并导入以下包：

from simpleai.search import astar, SearchProblem 

定义一个类，其中包含解决 8 难题的方法：

# Class containing methods to solve the puzzle 
class PuzzleSolver(SearchProblem): 

覆盖actions方法以使与当前问题保持一致：

 # Action method to get the list of the possible
    # numbers that can be moved into the empty space 
    def actions(self, cur_state):
        rows = string_to_list(cur_state)
        row_empty, col_empty = get_location(rows, 'e') 

检查空白区域的位置并创建新动作：

 actions = []
        if row_empty > 0:
            actions.append(rows[row_empty - 1][col_empty])
        if row_empty < 2:
            actions.append(rows[row_empty + 1][col_empty])
        if col_empty > 0:
            actions.append(rows[row_empty][col_empty - 1])
        if col_empty < 2:
            actions.append(rows[row_empty][col_empty + 1])
        return actions 

覆盖result方法。 将字符串转换为列表，然后提取空白区域的位置。 通过更新位置生成结果：

 # Return the resulting state after moving 
    # a piece to the empty space 
    def result(self, state, action):
        rows = string_to_list(state)
        row_empty, col_empty = get_location(rows, 'e') 
        row_new, col_new = get_location(rows, action)
        rows[row_empty][col_empty], rows[row_new][col_new] = \
                rows[row_new][col_new], rows[row_empty][col_empty]
        return list_to_string(rows) 

检查是否达到目标：

 # Returns true if a state is the goal state 
    def is_goal(self, state):
        return state == GOAL 

定义heuristic方法。 我们将使用启发式算法，通过曼哈顿距离计算当前状态与目标状态之间的距离：

 # Returns an estimate of the distance from a state to 
    # the goal using the manhattan distance
    def heuristic(self, state):
        rows = string_to_list(state) 

 distance = 0 

计算距离：

 for number in '12345678e':
            row_new, col_new = get_location(rows, number) 
            row_new_goal, col_new_goal = goal_positions[number]
            distance += abs(row_new - row_new_goal) + abs(col_new - col_new_goal) 

 return distance 

定义一个函数以将列表转换为字符串：

# Convert list to string
def list_to_string(input_list):
    return '\n'.join(['-'.join(x) for x in input_list]) 

定义一个将字符串转换为列表的函数：

# Convert string to list
def string_to_list(input_string): 
    return [x.split('-') for x in input_string.split('\n')] 

定义一个函数以获取给定元素在网格中的位置：

# Find the 2D location of the input element 
def get_location(rows, input_element):
    for i, row in enumerate(rows): 
        for j, item in enumerate(row):
            if item == input_element:
                return i, j 

定义我们想要实现的初始状态和最终目标：

# Final result that we want to achieve
GOAL = '''1-2-3
4-5-6
7-8-e''' 

# Starting point
INITIAL = '''1-e-2
6-3-4
7-5-8''' 

通过创建变量来跟踪每件作品的目标位置：

# Create a cache for the goal position of each piece
goal_positions = {}
rows_goal = string_to_list(GOAL)
for number in '12345678e':
    goal_positions[number] = get_location(rows_goal, number) 

使用我们先前定义的初始状态创建A*求解器对象，并提取结果：

# Create the solver object
result = astar(PuzzleSolver(INITIAL)) 

打印解决方案：

# Print the results
for i, (action, state) in enumerate(result.path()):
    print()
    if action == None:
        print('Initial configuration')
    elif i == len(result.path()) - 1:
        print('After moving', action, 'into the empty space. Goal achieved!')
    else:
        print('After moving', action, 'into the empty space') 

 print(state) 

完整代码在文件puzzle.py中给出。 如果运行代码，将得到很长的输出。

它将按以下方式启动：

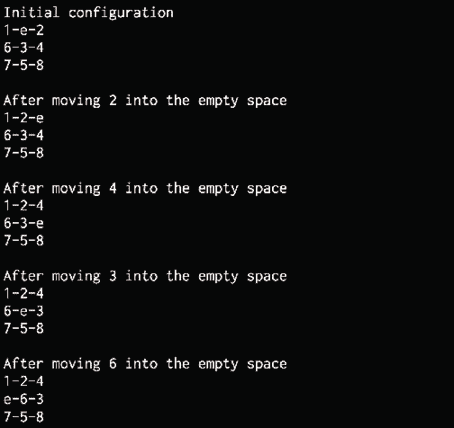
图 10：PuzzleSolver 输出

如果向下滚动，您将看到为解决方案而采取的步骤。 最后，您将看到以下内容：

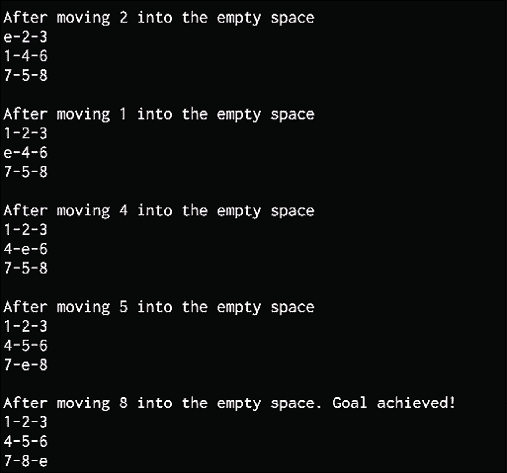
图 11：PuzzleSolver 输出的结尾-已实现目标！

如您所见，目标已实现，难题得以解决。

建立迷宫求解器

让我们使用A*算法来解决迷宫问题。 考虑下图：

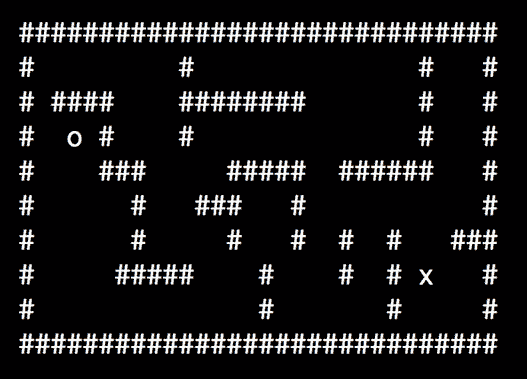
图 12：迷宫问题的示例

#符号表示障碍物。o代表起点，x代表目标。 目的是找到从起点到终点的最短路径。 让我们看看如何在 Python 中做到这一点。 以下解决方案是simpleai库中提供的解决方案的变体。 创建一个新的 Python 文件并导入以下包：

import math
from simpleai.search import SearchProblem, astar 

创建一个包含解决问题所需方法的类：

# Class containing the methods to solve the maze 
class MazeSolver(SearchProblem): 

定义初始化方法：

 # Initialize the class
    def __init__(self, board):
        self.board = board
        self.goal = (0, 0) 

提取初始位置和最终位置：

 for y in range(len(self.board)):
            for x in range(len(self.board[y])):
                if self.board[y][x].lower() == "o":
                    self.initial = (x, y)
                elif self.board[y][x].lower() == "x":
                    self.goal = (x, y) 

 super(MazeSolver, self).__init__(initial_state=self.initial) 

覆盖actions方法。 在每个位置，我们需要检查前往相邻单元的成本，然后附加所有可能的操作。 如果相邻单元被阻塞，则不考虑该操作：

 # Define the method that takes actions 
    # to arrive at the solution
    def actions(self, state):
        actions = []
        for action in COSTS.keys():
            newx, newy = self.result(state, action) 
            if self.board[newy][newx] != "#":
            actions.append(action) 

 return actions 

覆盖result方法。 根据当前状态和输入操作，更新x和y坐标：

 # Update the state based on the action 
    def result(self, state, action):
        x, y = state 

 if action.count("up"):
            y -= 1
        if action.count("down"):
            y += 1
        if action.count("left"):
            x -= 1
        if action.count("right"):
            x += 1 

 new_state = (x, y) 

 return new_state 

检查我们是否已经达到目标：

 # Check if we have reached the goal
    def is_goal(self, state):
        return state == self.goal 

我们需要定义cost函数。 这是移动到相邻单元的成本，并且垂直/水平和对角线移动是不同的。 我们将在以后定义这些：

 # Compute the cost of taking an action
    def cost(self, state, action, state2):
        return COSTS[action] 

定义将使用的试探法。 在这种情况下，我们将使用欧几里得距离：

 # Heuristic that we use to arrive at the solution 
    def heuristic(self, state):
        x, y = state
        gx, gy = self.goal 

 return math.sqrt((x - gx) ** 2 + (y - gy) ** 2) 

定义main函数并定义我们前面讨论的映射：

if __name__ == "__main__":
    # Define the map
    MAP = """
    ##############################
    #         #              #   #
    # ####    ########       #   #
    #  o #    #              #   #
    #    ###     #####  ######   #
    #      #   ###   #           #
    #      #     #   #  #  #   ###
    #     #####    #    #  # x   #
    #              #       #     #
    ##############################
    """ 

将地图信息转换为列表：

 # Convert map to a list 
    print(MAP)
    MAP = [list(x) for x in MAP.split("\n") if x] 

定义在地图上移动的成本。 对角线移动比水平或垂直移动更昂贵：

 # Define cost of moving around the map
    cost_regular = 1.0
    cost_diagonal = 1.7 

将成本分配给相应的移动：

 # Create the cost dictionary 
    COSTS = {
        "up": cost_regular,
        "down": cost_regular,
        "left": cost_regular,
        "right": cost_regular,
        "up left": cost_diagonal,
        "up right": cost_diagonal,
        "down left": cost_diagonal,
        "down right": cost_diagonal,
    } 

使用先前定义的自定义类创建一个求解器对象：

 # Create maze solver object
    problem = MazeSolver(MAP) 

在地图上运行求解器并提取结果：

 # Run the solver
    result = astar(problem, graph_search=True) 

从结果中提取路径：

 # Extract the path
    path = [x[1] for x in result.path()] 

打印输出：

 # Print the result
    print()
    for y in range(len(MAP)):
        for x in range(len(MAP[y])):
            if (x, y) == problem.initial:
                print('o', end='')
            elif (x, y) == problem.goal:
                print('x', end='')
            elif (x, y) in path:
                print('·', end='')
            else:
                print(MAP[y][x], end='') 

 print() 

完整代码在文件maze.py中给出。 如果运行代码，将得到以下输出：

图 13：迷宫问题的解决方案

如您所见，算法留下了一点点的痕迹，并找到了从起点o到终点x的解。 至此，本章最后部分总结了A*算法的迷宫解决方案。

总结

在本章中，我们学习了启发式搜索技术的工作原理。 我们讨论了不知情和知情搜索之间的区别。 我们了解了约束满足问题，以及如何使用此范式解决问题。 我们讨论了本地搜索技术如何工作以及为什么在实践中使用了模拟退火。 我们对字符串问题实现了贪婪的搜索。 我们使用 CSP 公式解决了一个问题。

我们使用这种方法来解决区域着色问题。 然后，我们讨论了A*算法及其如何用于找到解决方案的最佳路径。 我们用它来构建 8 难题求解器和迷宫求解器。 在下一章中，我们将讨论遗传算法及其如何用于解决现实世界中的问题。

标签：10,plt,Python,数据,人工智能,print,import,data,我们
From： https://www.cnblogs.com/apachecn/p/17322101.html