线索二叉树与哈夫曼树
线索二叉树
-
线索二叉树的概念
- 采用某种方法遍历二叉树的结果是一个结点的线性序列。
- 修改空链域改为存放指向结点的前驱和后继结点的地址。
- 这样的指向该线性序列中的”前驱“和”后继“的指针,称作线索(thread)。
- 创建线索的过程称为线索化。
- 线索化的二叉树称为线索二叉树。
- 显然线索二叉树与采用的遍历方法相关,有先序线索二叉树、中序线索二叉树和后续线索二叉树。
- 线索二叉树的目的是提高该遍历过程的效率。
在结点的存储结构上增加了两个标志位来区分这两种情况:
左标志ltag:0表示lchild指向左孩子结点/1表示lchild指向前驱结点,即线索
右标志rtag:0表示rchild指向右孩子结点/1表示rchild指后继结点,即线索
这样,每个结点的存储结构如下:
ltag lchild data rchild rtag 为了方便算法计算,在线索二叉树中再增加一个头结点。
线索化二叉树中结点的类型定义如下:
typedef struct node { Elemtype data;//结点的数据域 int ltag, rtag;//增加的线索标志 struct node *lchild;//左孩子或线索指针 struct node *rchild;//右孩子或线索指针 }TBTNode; //线索树结点类型定义 -
线索化二叉树
建立某种次序的线索二叉树过程:
- 以该遍历方法遍历一颗二叉树。
- 在遍历的过程中,检查当前访问结点的左、右指针域是否为空:
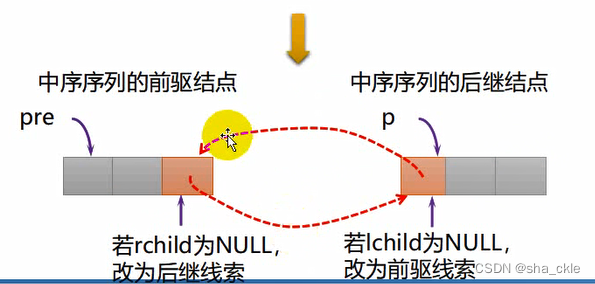
- 如果左指针域为空,将它改为指向前驱结点的线索;
- 如果右指针域为空,将它改为指向后继结点的线索。
-
建立中序线索二叉树的算法
- CreatThread(b)算法:对以二叉存储的二叉树b进行中序线索化,并返回线索化后头结点的指针root。
- Thread(p)算法:对以*p为根结点的二叉树子树的中序线索化。
在中序遍历当中:
- P总是指向当前线索化地结点。
- pre作为全局变量,指向刚刚访问过的结点、
- *pre是*p的中序前驱结点,*p是*pre的中序后继结点。
-
遍历线索化二叉树
遍历某种次序的线索二叉树,就是从该次序下的开始结点出发,反复找到该结点在该次序下的后继结点,直到头结点。
以中序线索二叉树为例,开始结点是根节点的最左下结点。
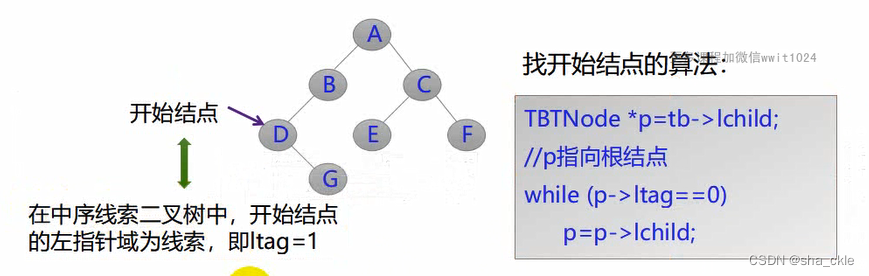
在中序线索二叉树中中序遍历的过程:
p指向根结点;
while p ≠ root时循环
{
找开始结点*p;
访问*p结点;
while(*p结点有右线索)
一直访问下去;
p转向右孩子结点;
}
哈夫曼树
-
哈夫曼树的定义
设二叉树具有n个带权值的叶结点,那么从根节点到各个叶结点的路径长度与相应结点权值的乘积和,叫做二叉树的带权路径长度。
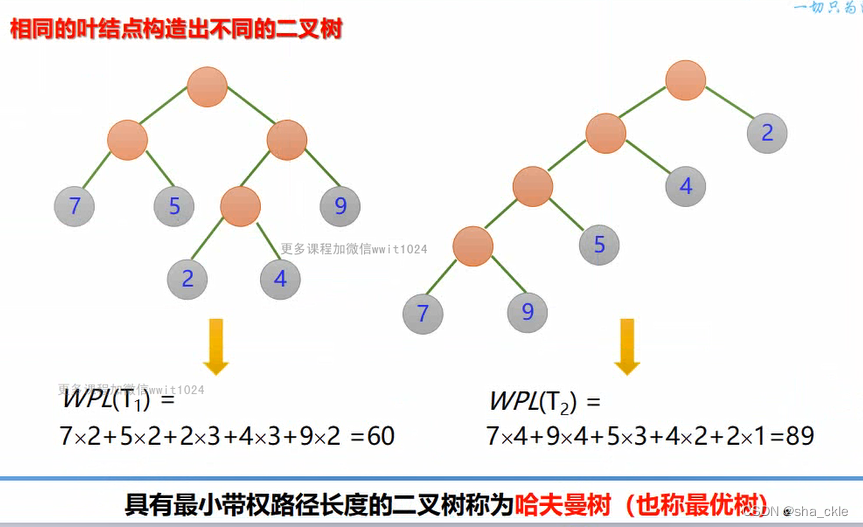
-
构造哈夫曼树的原则:
- 权值越大的叶结点越靠近根结点
- 权值越小的叶节点越远离根结点
构造哈夫曼树的过程:
- 给定的n个权值{W1,W2,...,Wn}构造n棵只有一个叶节点的二叉树,从而得到一个二叉树的集合F=
- 在F中选取根结点的权值最小和次小的两棵二叉树作为左、右子树构造一棵新的二叉树,这棵新的二叉树根据结点的权值为其作、右子树根节点权值之和
- 在集合F中删除作为左、右子树的两棵二叉树,并将新建立的二叉树加入到集合F中。
- 重复(2)、(3)两步,当F中只剩下一颗二叉树时,这棵二叉树便是所要建立的哈夫曼树。
-
哈夫曼编码
规定哈夫曼树中的左分支为0,右分支为1(哈夫曼编码属0、1二进制编码),则从根节点到每个叶节点所经过的分支对应的0和1组成的序列变为该结点对应的字符的编码。这样的编码称为哈夫曼编码。
图及图的存储结构
图的基础知识
-
图的定义:图(Graph)G由顶点集合V(G)和边集合E(G)构成。
说明:对于n个顶点的图,对每个顶点连续编号,即顶点的编号为0~n-1。通过编号唯一确定一个顶点。
图抽象数据类型=逻辑结构+基本运算(运算描述)
图的基本运算如下:
- InitGraph(&g):图初始化、
- ClaerGraph(&g):销毁图、
- DFS(G,V):从顶点v出发深度优先遍历
- BFS(G,V):从顶点v出发广度优先遍历
如图G中,如果代表边的顶点对是无序的,则称G为无向图。用圆括号序偶表示无向边。
如果表示边的顶点对是有序的,则称G为有向图。用尖括号序偶表示有向边。
-
图的基本术语
【端点和邻接点】
- 无向图:若存在一条边(i,j)——>顶点i和顶点j为端点,它们互为邻接点。
- 有向图:若存在一条边<i,j>——>顶点i为起始端点(简称为起点),顶点j为终止端点(简称终点),它们互为邻接点。
【顶点的度、入度和出度】
- 无向图:以顶点i为端点的边数称为该顶点的度。
- 有向图:以顶点i为终点的入边的数目,称为该顶点的入度。以顶点i为终点的出边的数目,称为该顶点的出度。一个顶点的入度和出度和和为该顶点的度。
-
完全图
- 无向图:每两个顶点之间都存在着一条边,称为完全无向图,包含有n(n-1)/2条边
- 有向图:每两个顶点之间都存在着方向相反的两条边,称为完全有向图,包含有n(n-2)条边。
-
稠密图、稀疏图
当一个图接近完全图时,则称为稠密图
相反,当一个图含有较少的边数(即当e<<n(n-1))时,则称为稀疏图。
-
子图
设有两个图G=(V,E)和G`=(V`,E`),若V`是V的子集,则E`是E的子集,则称G`是G的子图。
-
回路或环
若一条路径上的开始点与结束点为同一个顶点,则此路径被称为回路或环。开始点与结束点相同的简单路径被称为简单回路或简单环。
-
连通、连通图和连通分量
无向图:若从顶点i到顶点j有路径,则称顶点i和j是连通的。
若图中任意两个顶点都连通,则称为连通图,否则称为非连通图。
无向图G中的极大连通子图称为G的连通分量。显然,任何一个连通图的连通分量只有一个,即本身,而非连通图有多个连通分量。
-
强连通图和强连通分量
有向图:若从顶点i到顶点j有路径,则称从顶点j到j是连通的。
若图G中的任意两个顶点i和j都连通,即从顶点i到j和从顶点j到i都存在路径,则称图G是强连通图。
-
权和网
图中每一条边都可以附带有一个对应的数值,这种与边相关的数值称为权。权可以表示从一个顶点到另一个顶点的距离或花费的代价。
边上带有权的图称为带权图,也称为网。
图的存储结构
图的逻辑结构—(映射)—>图的存储结构(存储每个顶点的信息、存储每条边的信息)
图的两种主要存储结构:邻接矩阵、邻接表。
-
邻接矩阵存储方法
邻接矩阵是表示顶点之间相邻关系的矩阵。G=(V,E)是具有n(n>0)个顶点的图,顶点的编号依次为0~n-1。
G是邻接矩阵A是n阶方针,其定义如下:
- 如果G是无向图,则:A[i][j]=1:若(i,j)∈E(G) 0:其他
- 如果G是有向图,则:A[i][j]=1:若<i,j>∈E(G) 0:其他
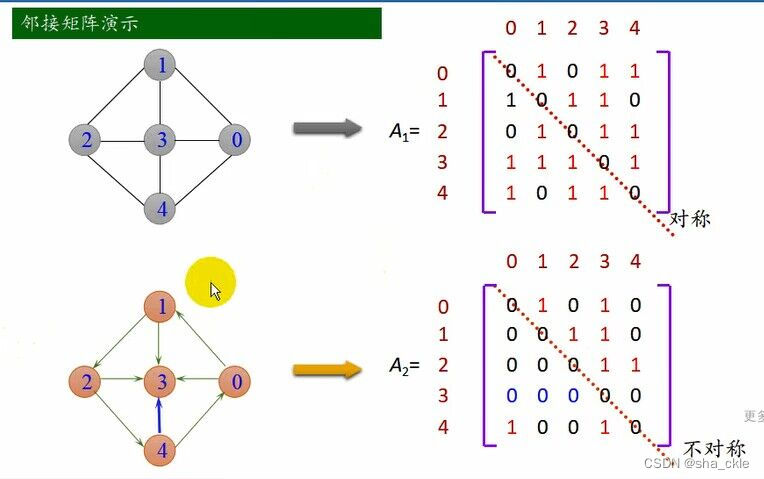
邻接矩阵的主要特点:
一个图是邻接矩阵表示是唯一的;特别适合于稠密图的存储。
图的邻接矩阵存储类型定义如下:
define MAXV<最大顶点个数>
typedef struct//声明顶点类型
{
int no;//顶点编号
Info Type info;//顶点其他信息
}VertexType;
typedef struct//声明的邻接矩阵类型
{
int edges[MAXV][MAXV];//邻接矩阵
int n, e;//顶点数、边数
VertexType vexs[MAXV];//存放顶点信息
}MatGraph;
-
邻接表存储方法
对图中每个顶点i建立一个单链表,将顶点i的所有邻接表链起来。
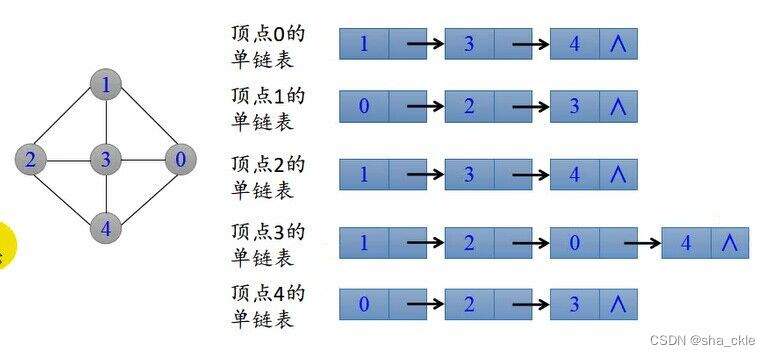
每个单链表上添加一个表头结点(表示顶点信息)。并将所有头结点构成一个数组,下标为i的元素表示顶点为i的表头结点。
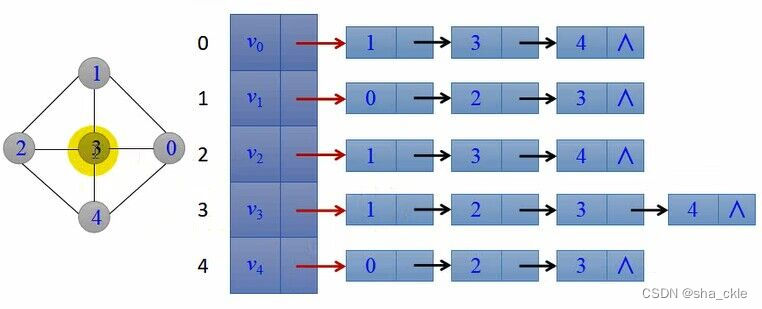
邻接表的特点如下:
邻接表表示不唯一;特别适合稀疏图的存储。
图的邻接表存储类型定义如下:
typedef struct ANode//声明边结点类型
{
int adjvex;//该边的终点编号
struct ANode *nextarc;//指向下一条边的指针
InfoType info;//该边的权值等信息
}ArcNode;
typedef struct Vnode//声明邻接表头结点类型
{
Vertex data;//顶点信息
ArcNode *firstarc;//指向第一条边
}VNode;
typedef struct//声明图邻接表类型
{
VNode adjlist[MAXV];//邻接表
int n, e;//图中顶点数n和边数e
}AdjGraph;
逆邻接表:就是在有向图的邻接表中,对每个顶点,链接的是指向该顶点的边。
深度优先搜索及广度优先搜索
深度优先搜索(DFS-Depth_First Search)
基本思想:——仿照的先序遍历过程
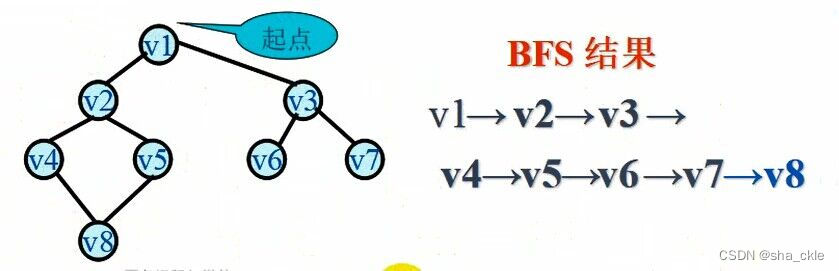
【深度优先搜索的步骤】
简单归纳:
- 访问起始点V;
- 若V的第1个邻接点没访问过,深度遍历此邻接点;
- 若当前邻接点已访问过,再找V的第2个邻接点重新遍历。
详细归纳:
-
在访问图中某一个起始顶点V后,由V出发,访问它的任一邻接顶点w1;
-
再从w1出发,访问与w1邻接但未被访问过的顶点w2;
-
然后再从w2出发,进行类似的访问,...
-
如此进行下去,直至到达所有的邻接顶点都被访问过的顶点u为止。
-
接着,退回一步,退到前一次刚访问过的顶点,看是否还有其它没有被访问的邻接顶点。
如果有,则访问此顶点,之后再从此顶点出发,进行与前述类似的访问;
如果没有,就再退回一步进行搜索。重复上述过程,直到连通图中所有顶点都被访问过为止。
广度优先搜索(BFS-Breadth_First Search)
基本思想——仿树的层次遍历过程
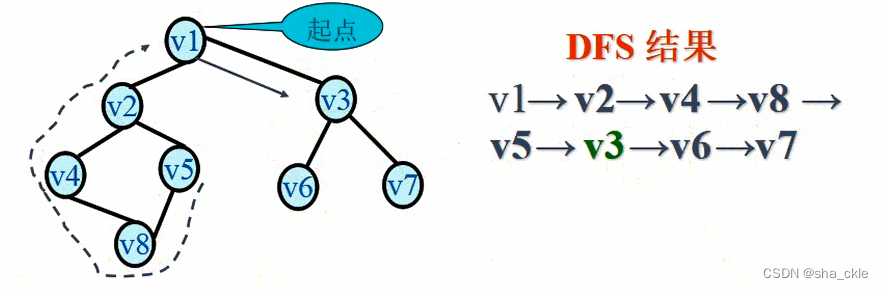
【广度优先搜索的步骤】
简单归纳:
- 在访问了起始点v之后,依次访问v的邻接点;
- 然后再依次访问这些顶点中未被访问过的邻接点;
- 直到所有顶点都被访问过为止。
广度优先搜索是一种分层的搜索过程,每向前走一步可能访问一批顶点,不像深度优先搜索那样有回退的情况
因此,广度优先搜索不是一个递归的过程,其算法也不是递归的。
【算法思想】
- 从图中某个顶点v出发,访问v,并置visited[v]的值为true,然后将v进队。
- 只要队列不空,则重复下述处理。
- 队头顶点u出队
- 依次检查u的所有邻接点w,如果visited[w]的值为false,则访问w,并置visited[w]的值为true,然后将w进队。
网络爬虫软件:1. 广度优先搜索算法 2. 深度优先搜索算法。
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#define ElemType char;
//初始化队头和队尾指针置为0
int front = 0, rear = 0;
typedef struct BitreeNode{
ElemType data;//数据域
struct BitreeNode *lchild, *rchild;//左右指针
}BitreeNode, *BiNode;
void CreateBinTreeFunc(BiNode *T)
{
*T = (BitreeNode*)malloc(sizeof(BitreeNode));
(*T)->data = 'A';
(*T)->lchild = (BitreeNode*)malloc(sizeof(BitreeNode));
(*T)->rchild = (BitreeNode*)malloc(sizeof(BitreeNode));
(*T)->lchild->data = 'B';
(*T)->rchild->data = 'C';
(*T)->lchild->lchild = (BitreeNode*)malloc(sizeof(BitreeNode));
(*T)->lchild->rchild = (BitreeNode*)malloc(sizeof(BitreeNode));
(*T)->lchild->lchild->data = 'D';
(*T)->lchild->lchild->lchild = NULL;
(*T)->lchild->lchild->rchild = NULL;
(*T)->lchild->rchild->data = 'E';
(*T)->lchild->rchild->lchild = NULL;
(*T)->lchild->rchild->rchild = NULL;
(*T)->rchild->lchild = (BitreeNode*)malloc(sizeof(BitreeNode));
(*T)->rchild->rchild = (BitreeNode*)malloc(sizeof(BitreeNode));
(*T)->rchild->lchild->data = 'F';
(*T)->rchild->lchild->lchild = NULL;
(*T)->rchild->lchild->rchild = NULL;
(*T)->rchild->rchild->data = 'G';
(*T)->rchild->rchild->lchild = NULL;
(*T)->rchild->rchild->rchild = NULL;
}
//入队操作
void EnterQueueFunc(BiNode *x, BiNode node)
{
x[rear++] = node;
}
//出队操作
BitreeNode *DeleteQueueFunc(BitreeNode**x)
{
return x[front++];
}
//输出数据元素
void printNodeData(BiNode node)
{
printf("%c ",node->data);
}
int main()
{
BiNode tree;
//初始化树
CreateBiTreeFunc(&tree);
BitreeNode *p;
BiNode x[50];
EnterQueueFunc(x, tree);
printf("广度优先搜索算法输出的结果");
while(front < rear)
{
p = DeleteQueueFunc(x);
PrintNodeData(p);
if(p->lchild != NULL)
EnterQueueFunc(x, p->lchild);
if(p->rchild != NULL)
EnterQueueFUnc(x, p->rchild);
}
}
最小生成树及最短路径算法
最小生成树
一个连通图的生成树是一个极小连通图,它含有图中全部n个顶点和构成一棵树的(n-1)条边。
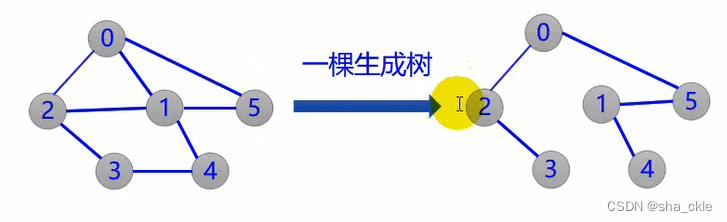
命题:如果在一棵生成树上添加一条边,必定构成一个环。
可以通过遍历方法产生生成树:
由深度优先算法遍历得到的生成树称为深度优先生成树。
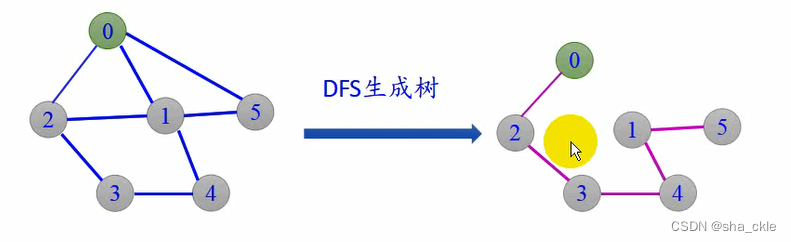
由广度优先遍历得到的生成树称为广度优先生成树
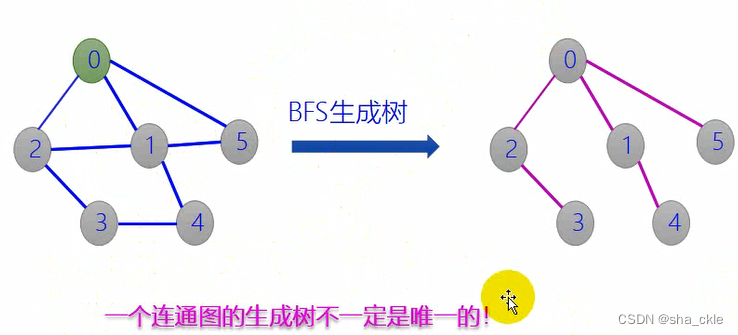
【最小生成树的概念】
- 对于带权连通图G(每条边上的权均大于零的实数),可能有多棵不同生成树
- 每棵生成树的所有边的权值之和可能不同
- 其中权值之和最小的生成树称为图的最小生成树。
【非连通图和生成树】
连通图:仅需调用遍历过程(DFS或BFS)一次、从图中任一顶点出发,便可以遍历图中的各个顶点,产生相应的生成树。
非连通图:需多次调用遍历过程。每个连通分量中的顶点集和遍历时走过的边一起构成一棵生成树。所有连通分量的生成树组成非连通图的生成森林。
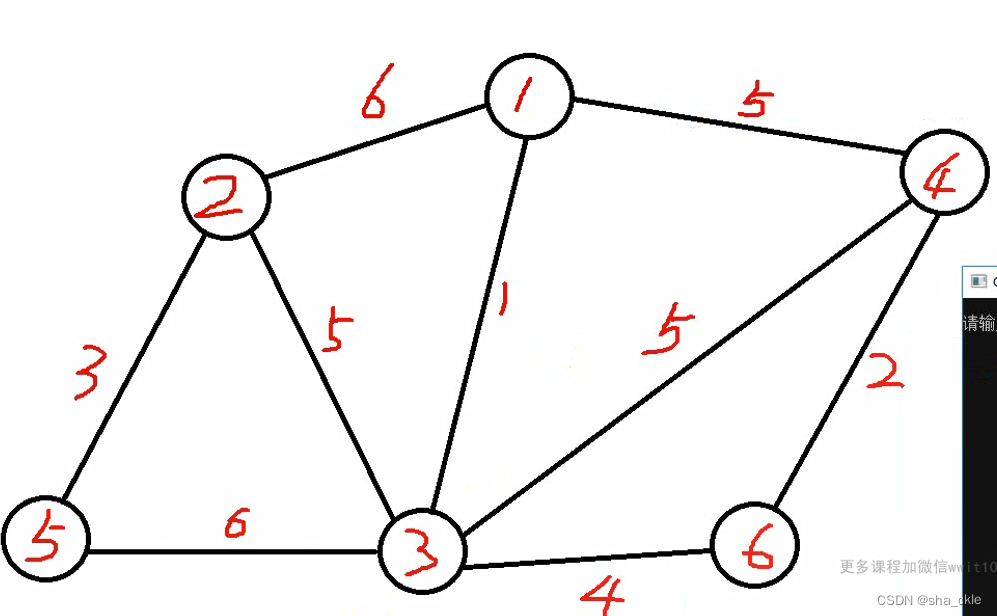
重点:求带权连通图的最小生成树。
【普里姆算法】
普里姆(prim)算法是一种构造性算法,用于构造最小生成树。过程如下:
- 初始化U={v}。v到其他顶点的所有边为侯选边;
- 重复一下步骤n-1次,使得其他n-1个顶点被加入到U中:
- 从侯选边中挑选权值最小的边输出,设该边在V-U中的顶点是k,将k加入到U中;
- 考察当前V-U中的所有顶点j,修改侯选边:若(j,k)的权值小于原来和顶点k关联的侯选边,则用(k,j)取代后者作为侯选边。
最短路径算法
用于计算一个结点到其他所有结点的最短路径。主要特点是以起始点为中心向外层扩展,直到扩展到终点为止。
dijkstra算法能得到最短路径的最优解,但由于它遍历计算的结点很多,所以效率很低。
- 在非网图中,最短路径是指两顶点之间经历的边数最少的路径。(非网图:没有权值)
- 在网图中,最短路径是指两顶点之间经历的边上权值之后最短的路径。
1.【单源点最短路径问题】
问题描述:给定带权有向图G=(V,E)和源点v∈V,求从v到G中其余各顶点的最短路径。
应用实例——计算机网络传输问题:怎样找到一种最经济的方式,从一台计算机向网上所有其它计算机发送一条消息。
2.【每一对顶点之间的最短路径】
问题描述:给定带权有向图G=(V,E),对任意顶点vi,vj∈V(i≠j),求顶点vi到顶点vj的最短路径。
解决方法1:每次以一个顶点为源点,调用Dijkstra算法n次。
3.【Dijkstra算法】
- 基本思想:设置一个集合S存放已经找到最短路径的顶点,S的初始状态只包含源点v,对vi∈V-S,假设从源点v到vi的有向边为最短路径。以后每求的一条最短路径v,...,vk,就将vk加入集合S中,并将路径v,...,vk,vi与原来的假设相比较,取路径长度较小者为最短路径。重复上述过程,直到集合V中全部顶点加入到集合S中。
- 设计数据结构:
- 图的存储结构:带权的邻接矩阵存储结构
- 数组dist[n]:每个分量dist[i]表示当前所找到的从初始点v到终点vi的最短路径的长度。初始态为:若从v到vi有弧,则dist[i]为弧上权值;否则置dist[i]为无穷。
- 数组path[n]:path[i]是一个字符串,表示当前所找到的从初始点v到终点vi的最短路径。初始态为:若从v到vi有弧,则path[i]为wi;否则置path[i]空串。
- 数组s[n]:存放源点和已经生成的终点,其初态为只有一个源点v。
#include<iostream>
#include<stdio.h>
#define MAX 50
#define MAXCOST 0xFFFFFFF
int graph[MAX][MAX];
void PrimFunc(int graph[][MAX], int n)
{
int lowcost[MAX];
int mst[MAX];
int min, minid, sum = 0;
for(i = 2; i <= n; i++)
{
lowcost[i] = graph[1][i];//lowcast存放顶点1可以到达点的路径长度
mst[i] = 1;//初始化以1位起始点
}
mst[i] = 0;
for(int i = 2; i <= n; i++)
{
min = MAXCOST;
minid = 0;
for(int j = 2; j <= n; j++)
{
if(lowcost[j] < min && lowcost[j] != 0)
{
min = lowcost[j];//找出权值最短的路径长度
minid = j;//找出最小的ID
}
}
printf("V&d-->V%d = %d\n", mst[minid], minid, min);
sum += min;//求和
lowcost[minid] = 0;//最短路径置为0
for(j = 2; j <= n; j++)
{
if(grap[minid][j] < lowcost[j])//对这一点直达顶点进行路径更新
{
lowcost[j] = graph[minid][j];
mst[j] = minid;
}
}
}
printf("最小权值之和为:%d\n", sum);
}
int main()
{
int i, j, k, m, n;
int x, y, cost;
printf("请输入顶点和边数\n");
scanf("%d%d",&m, &n);//m_顶点,n_边数
for(i = 1; i <= n; i++)
{
for(j = 1; j <= n; j++)
{
graph[i][j] = MAXCOST;
}
}
printf("请输入点到点之间名称及权值:\n");
for(k = 1; k <= n; k++)
{
scanf("%d%d%d", &i, &j ,&cost);
graph[i][j] = cost;
graph[j][i] = cost;
}
PrimFunc(graph,m);
return 0;
}
折半查找算法
折半查找
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
【查找过程】
首先,假设表中的元素时按升序排雷,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。
【算法要求】
- 必须采用顺序存储结构。
- 必须按关键字大小有序排列。
#include<iostream>
//定义折半查找算法
void BinSearchFunc(int a[], int key)
{
int low, high, mid, flag = 0;
low = 0;
high = 9;
while(low <= high)
{
mid = (low + high) / 2;
printf("low = %d, mid = %d, high = %d \n",low, mid, high);
if(a[mid] > key)
{
high = mid -1;
}
if(a[mid] < key)
{
low = mid + 1;
}
if(a[mid] = key)
{
flag = 1;
break;
}
}
if(flag)
{
printf("\n已经查找到该数字信息.\n\n");
}
else
{
printf("\n未查找到该数字信息.\n\n");
}
}
int main()
{
int a[10], num;
printf("\n请初始化数字a[10]\n");
for(int i = 0; i <= 9; i++)
{
scanf("%d", &a[i]);
}
printf("\n请输入要查找的数据:");
scanf("%d", &num);
BinSearchFunc(a, num);
return 0;
}
散列表(Hash)算法
散列表(Hash)
散列表(hash table,也叫哈希表),是根据关键码值(key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来记录访问记录,以加快查找的速度。这个映射函数也叫做叫做散列函数,存放记录的数组叫做散列表。
给定表M,存在函数(key),对任意给定的关键值key,代入函数后若能得到包含该关键字的记录在表中的地址,则称表M为哈希(Hash)表,函数f(key)为哈希(Hash)函数。
散列函数能使对一个数据序列的访问过程更加迅速有效,通过散列函数,数据元素将被更快地定位。
实际工作中需要不同的情况采用不同的哈希函数,通常考虑的因素有:
- 计算哈希函数所需时间
- 关键字的长度
- 哈希表的大小
- 关键字的分布情况
- 记录的查找频率
- 直接寻址法:取关键字或关键字的某个线性函数值为散列地址,即H(key)=key或H(key)=a.key + b,其中a和b为常数(这种散列函数叫做自身函数),若其中H(key)中已经有值了,就往下一个找,直到H(key)中没有值了,就放进去。
- 数字分析法:分析一组数据,比如一组员工的出生年月日,这是我们发现出生年月日的前几位数字大体相同,这样的话,出现冲突的几率就会很大,但是我们发现年月日的后几位表示月份和具体日期的数组差别很大,如果用后面的数字来构造散列地址,则冲突的几率会明显降低。因此数字分析法就是找出数字的规律,尽可能利用这些数据来构造冲突几率较低的散列地址。
- 平方取中法:当无法确定关键字中哪几位分布比较均匀时,可以先求出关键字的平方值,然后按需要取平均值的中间几位作为哈希地址。这是因为:平方后中间几位和关键字中每一位都相关,故不同关键字会以比较高的概率产生不同的哈希地址。
- 折叠法:将关键字分割成位数相同的几部分,最后一部分位数可以不同,然后取这几部分的叠加(去除进位)作为散列地址。数位叠可以有移位叠加和间界叠加两种方法。移位叠加是将分割后的每一部分的最低位对齐,然后相加;间界叠加是从一端向另一端沿分割界来回折叠,然后对齐相加。
- 随机数法:选择一随机数,取关键字的随机值作为散列地址,即H(key)=random(key)其中random为随机函数,通常用于关键字长度不等的场合。
- 除留余数法:取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。即H(key) = key MOD p, p<=m。不仅可以对关键字直接取模,也可在折叠、平方取中等运算之后取模。对p的选择很重要,一般取素数或m,若p选的不好,容易产生同义词。
#include<stdio.h>
#indlude<stdlib.h>
#define MAXSIZE 1000 //存储空间初始化分配量
#define TRUE 1
#define FALSE 0
#define HASHSIZE 12//定义哈希表长为数组的长度
#define NULLKEY -32768
//定义哈希表
typedef struct {
int *elem;//数据元素存储基址,动态分配数组
int count;//当前数据元素个数
}HashTable;
typedef int Status;//Status是函数的类型,其值是函数结果状态代码,TRUE,FALSE
int m = 0;//哈希表表长 全局变量
Status InitHashTable(HashTable *hash);//初始化哈希表
int HashFunc(int key);//构造哈希函数
void InsertHash(HashTable *hash, int key);//插入关键字进哈希表
Status FindHashFunc(HashTable hash, int key, int *addr);//哈希查找关键字
Status InitHahtable(HashTable *hash)
{
int i;
m = HASHSIZE;
hash->count = m;
hash->elem = (int *)malloc(m * sizeof(int));
for(i = 0; i < m; i++)
{
hash->elem[i] = NULLKEY;
}
return TRUE;
}
int HashFunc(int key)
{
return key % m;//构造方法为除留余数法
}
void InsertHash(HashTable *hash, int key)
{
int addr = HashFunc(key);//求哈希地址
while(hash->elem[addr] != NULLKEY)//如果不为空,则冲突
{
addr = (addr + 1) % m;//开放定制法线性探测
}
hash->elem[addr] = key;//直到有空位之后插入关键字
}
Status FindHashFunc(HashTable hash, int key, int *addr)
{
*addr = HashFunc(key);//求哈希地址
while(hash.elem[*addr] != key) //否则,使用开放定址法继续查找
{
*addr = (*addr + 1) % m;//开发定址法的线性探测
if(hash.elem[*addr] == NULLKEY || *addr = HashFunc(key))
{
return FALSE;
}
}
return TRUE;
}
int main()
{
int a[HASHSIZE] = {12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 35};//插入的关键字
int key = 37; //关键字
int addr;//哈希地址
HashTable hash;
//初始化哈希表
InitHashTable(&hash);
//插入关键字到哈希表
for(int i = 0; i < m; i++)
InsertHash(&hash, a[i]);
//查找key为37的关键字
int rs = FindHashFunc(hash, key, &addr);
if(rs)
printf("\n查找%d的哈希地址为:%d\n\n",key , addr);
else
printf("\n查找%d失败,\n\n",key);
//遍历查找关键字(都会成功)
for(int i = 0; i < m; i++)
{
key = a[i];
FindHashFunc(hash, key, &addr);
printf("\n查找%d的哈希地址为:%d\n\n",key , addr);
}
printf("\n");
return 0;
}
插入排序与快速排序
插入排序
插入排序,一般也称为直接插入排序。对于少量元素的排序,它是一个有效的算法。插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增1的有序表。在其实现过程中使用双层循环,外层循环除了第一个元素之外的所有元素,内层循环对当前元素前面的有序表进行待插入位置查找,并进行移动。
应用分析:插入排序适用于已经有部分数据已经排好,并且排好的部分越大越好。一般在输入规模大于1000的场合下不建议使用插入排序。
#include<stdio.h>
void InsertSort(int a[], int n);
void SwapFunc(int *x, int *y);
void InsertSort(int a[], int n)
{
for(int i = 1; i < n; i++)
{
for(int j = i; j > 0 && a[j] < a[j - 1]; j--)
{
SwapFunc(&a[j], &a[j -1]);
}
}
}
void SwapFunc(int *x, int *y)
{
int t = *x;
*x = *y;
*y = t;
}
int main()
{
int a[7] = {12, 23, 65, 81, 22, 28, 98};
InsertSort(a, 7);
for(int i = 0; i < 7; i++)
printf("%d ", a[i]);
printf("\n");
return 0;
}
快速排序
快速排序(Quicksort)是对冒泡排序的一种改进
它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对着两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序算法通过多次比较和交换来实现排序,其排序流程如下:
- 首先设定一个分界值,通过该分界值将数组分成左右两部分。
- 将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分各元素都小于或等于分界值,而右边部分中各元素都大于或等于分界值。
- 然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以作类似处理。
- 重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后,整个数组的排序也就完成了。
#include<stdio.h>
void KSSortFunc(int a[], int low, int high)
{
if(high < low)
return;
int i = low;
int j = high + 1;
int key = a[low];
while(true)
{
//从左向右比Key大的值
while(a[++i] < key)
{
if(i == high)
break;
}
//从右向左比Key小的值
while(a[--j] > key)
{
if(j == low)
break;
}
if(i >= j)
break;
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
//中界值与j对应值交换
int temp = a[low];
a[low] = a[j];
a[j] = temp;
KSSortFunc(a, low, j-1);
KSSortFunc(a, j + 1, high);
}
int main()
{
int a[] = {57, 68, 59, 32, 73, 28, 97, 33, 25};
KSSortFunc(a, 0, sizeof(a)/sizeof(a[o]) -1);//三个参数要赋值
for(int i = 0; i < sizeof(a)/sizeof(a[0]); i++)
printf("&d-->",a[i]);
return 0;
}
希尔排序与选择排序
希尔排序
希尔排序(Shell`s Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键字越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率。
但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位。
算法思想:
希尔排序是特殊的插入排序,直接插入排序每次插入前的遍历步长为1,而希尔排序的将待排序列分为若干个子序列,对这些子序列分别进行直接插入排序,当每个子序列长度为1时,再进行一次直接插入排序时,结果一定是有序的。常见的划分子序列的方法有:初始步长(两个子序列相应元素相差的距离)为要排的数的一半,之后每执行一次步长折半。
#include<stdio.h>
#include<malloc.h>
void ShellSortFunc(int *p, int len);//函数声明
int _tmain(int argc, _TCHAR* argv[])
{
int i. len, *p;
printf("请输入要排序的数字个数:");
scanf_s("%d", &len);
p = (int*)malloc(len*sizeof(int));//动态定义数组
printf("请输入要排的数字:\n");
for(i = 0; i < len; i++)
scanf_s("%d", &p[i]);
ShellSortFunc(p ,len);
printf("希尔升序排序之后输出的结果为:\n");
for(i = 0; i < len; i++)
printf("%d\t",p[i]);
return 0;
}
void ShellSortFunc(int *p, int len)
{
int temp, gap, i, j, k;//gap为步长
for(gap = len / 2; gap > 0; gap /= 2)//步长初始化为数组长度的一半,每次遍历后步长减半
{
for(i = 0; i < gap; i++)//变量i为每次分组的下一个元素下标
{
for(j = i + gap; j < len; j += gap)//对步长为gap的元素进行直接排序,当gap为1时,就是直接排序
{
temp = p[j];//备份p[i]的值
k = j - gap;//j初始化为i的前一个元素(与i相差gap长度
while(k >= 0 && p[k] > temp)
{
p[k + gap] = p[i];//将在p[i]前且比temp的值大的元素向后移动一位
k -= gap;
}
p[k + gap] = temp;
}
}
}
}
选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。
【算法思想】
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
#include"stdafx.h"
#define ARRSIZE(arr) (sizeof(arr)/sizeof(arr[0]))
#define SWAP(X,Y) X=X+Y;Y=X-Y;X=X-Y;
void SelectSortFunc(int a[], int len);
void PrintFunc(int a[], int len);
int _tmain(int argc, _THCHAR* argv[])
{
int a[] = {23, 4, 7, 67, 45, 3, 453, 47, 67, 4, 53, 43, 43};
int len = ARRSIZE(a);
printf("\n排序之前数据输出如下:\n");
PrintFunc(a, len);
SelectSortFunc(a, len);
printf("\n排序之后数据输出如下:\n");
PrintFunc(a, len);
return 0;
}
void SelectSortFunc(int a[], int len)
{
int min;
for(int i = 0; i < len -1; i++)
{
min = i;
for(int j = i + 1; j < len; j++)
{
if(a[j] < a[min])
{
min = j;
}
}
if(min != i)
{
swap(a[i], a[min]);
}
}
}
void PrintFunc(int a[], int len)
{
for(int i = 0; i < len; i++)
{
printf("%5d", a[i]);
}
printf("\n");
}
冒泡排序与并归排序
冒泡排序
冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。
它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序(如从大到小、首字母从Z到A)错误就把它们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说元素列已经排序完成。
这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名”冒泡排序“。
【算法原理】
冒泡排序算法的原理如下:
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素做相同的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
#include"stdafx.h"
#include<stdio.h>
#define ARR_LEN 200 //数组长度上限
#define elemType int //元素类型
void BubbleSortFunc(elemType a[], int len)
{
ElemType temp;
for(int i = 0; i < len - 1; i++)//外循环是排序趟数,len个数进行len-1趟
{
for(int j = 0; j < len -i - 1; j++)//内循环是每趟比较的次数
{
if(a[j] > a[j + 1])//判断相信两个元素大小,决定是否交换它们的值
{
temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}
}
}
int _tmain(int argc, _TCHAR* argv[])
{
elemType a[ARR_LEN] = {43, 56, 88, 98, 67, 73, 26, 76, 44, 90};
printf("\n未排序之前输出的结果为:\n");
for(int i = 0; i < 10; i++)
printf("%d\t", a[i]);
printf("\n");
BubbleSortFunc(a, 10);
printf("\n排序之后输出的结果为:\n");
for(int i = 0; i < 10; i++)
printf("%d\t", a[i]);
return 0;
}
归并排序
归并排序(Merge Sort)是建立在归并操作上的一种有效,稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
【算法思想】
归并操作的工作原理如下:
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列。
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置。
- 比较两个指针所指的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置。
- 重复步骤3直到某一指针超出序列尾。
- 将另一序列剩下的所有元素直接复制到合并序列尾。
#include "stdafx.h"
#include<stdio.h>
#define N 10
//递归方式实现归并排序
//实现归并,把结果存放到List1
void MerFunc(int *list1, int list1_size, int *list2, int list2_size)
{
int i, j, k, m;
int temp[N];
i = j = k = 0;
while(i < list1_size && j < list2_size)
{
if(list1[i] < list2[j])
{
temp[k] = list1[i];
k++;
i++;
}
else
{
temp[k++] = list2[j++]
}
}
while(i < list1_size)
{
temp[k++] = list1[i++];
}
while(j < list2_size)
{
temp[k++] = list2[j++];
}
for(m = 0; m < (list1_size + list2_size); m++)
{
list1[m] = temp[m];
}
}
void Msort(int k[], int n)
{
if(n > 1)
{
//list1是左半部分,list2是右半部分
int *list1 = k;
int list1_size = n / 2;
int *list2 = k + list1_size;
int list2_size = n - list1_size;
Msort(list1, list1_size);
Msort(list2, list2_size);
MerFunc(list1, list1_size, list2, list2_size);
}
}
int _tmain(int argc, _TCHAR* argv[])
{
int a[10] = {34,54,67,87,12,43,56,90,56,76};
printf("\n未排序之前输出的结果为:\n");
for(int i = 0; i < 10; i++)
printf("%d\t", a[i]);
printf("\n");
Msort(a, 10);//调用归并算法
printf("\n排序之后输出的结果为:\n");
for(int i = 0; i < 10; i++)
printf("%d\t", a[i]);
return 0;
}
堆排序算法
堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子节点的键值或索引总是小于(或者大于)它的父节点。
【堆操作】
在堆的数据结构中,堆中的最大值总是位于根结点(在优先队列中使用堆的话堆中的最小值位于根结点)。堆中定义了以下几种操作:
- 最大堆调整(Max Heapify):将堆的末端子节点作调整,使得子节点永远小于父节点
- 创建最大堆(Build Max Heap):将堆中的所有数据重新排序
- 堆排序(HeapSort):移位在第一个数据的根结点,并做最大堆调整的递归运算。
#include"stdfax.h"
#include<stdio.h>
void SwapFunc(int *x, int *y)
{
int temp = *y;
*x = *y;
*x = temp;
}
void Max_heap(int a[], int start, int end)
{
//建立父节点指标和子节点指标
int dad = start;
int son = dad * 2 + 1;
//若子节点指标在范围内才做比较
while(son <= end)
{
fi(son + 1 <= end && a[son] < a[son + 1])//先比较两个子节点大小,选择最大的
son++;
if(a[dad] > a[son])//如果父节点大于子节点代表调整完毕,直接跳出函数
return;
else//否则交换父子内容再继续子节点和孙结点比较
{
SwapFunc(&a[dad], &a[son]);
dad = son;
son = dad * 2 + 1;
}
}
}
void Head_Sort(int a[], int len)
{
//初始化i从最后一个父节点开始调整
for(int i = len / 2 - 1; i >= 0; i--)
{
Max_heap(a, i, len - 1);
}
//先将第一个元素和已排好元素前一位做交换,再重新调整,直到排序完毕
for(int i = len - 1; i > 0; i--)
{
SwapFunc(&a[0], &a[i]);
Max_heap(a, 0, i - 1);
}
}
int _tmain(int argc, _THCHAR* argv[])
{
int a[] = {-90, 23, 54, 65, 78, 96, 23, 45, 68, 13};
int len = (int)sizeof(a) / sizeof(*a);
printf("\n未排序之前输出的结果为:\n");
for(int i = 0; i < len; i++)
printf("%d\t", a[i]);
printf("\n");
Head_Sort(a, len);//调用归并算法
printf("\n排序之后输出的结果为:\n");
for(int i = 0; i < len; i++)
printf("%d\t", a[i]);
return 0;
}