算法随想Day30【贪心算法】| LC1005-K次取反后最大化的数组和、LC134-加油站、LC135-分发糖果

LC1005. K 次取反后最大化的数组和

借用评论区的一句话——“普通人思维，无数个if else”。

void NegationsLoop(vector<int>& nums, int k, int pos)
{
    if (k % 2 != 0)
        nums[pos] = -nums[pos];
}

int largestSumAfterKNegations(vector<int>& nums, int k)
{
    int NumNegative = 0;
    sort(nums.begin(), nums.end());
    for (int i = 0; i < nums.size(); ++i)
    {
        if (nums[i] >= 0)
        {
            break;
        }
        ++NumNegative;
    }
    if (NumNegative == 0)
    {
        NegationsLoop(nums, k, 0);
    }
    else 
    {
        if (NumNegative >= k)
        {
            for (int pos = 0; pos < k; ++pos)
                nums[pos] = -nums[pos];
        }
        else if (k > NumNegative)
        {
            int pos;
            for (pos = 0; pos < NumNegative; ++pos)
                nums[pos] = -nums[pos];
            //-4,-3,-1,2,5  k = 15  或  -4,-3,-1  k = 4
            if ((pos > 1 && nums[pos] > nums[pos - 1]) || pos >= nums.size())  
            {
                --pos;
            }
            NegationsLoop(nums, k - NumNegative, pos);
        }
    }

    int sum = 0;
    for (int i = 0; i < nums.size(); ++i)
        sum += nums[i];
    return sum;
}

Carl哥思路，对整个数组以绝对值的大小进行降序排列，妙不可言

int largestSumAfterKNegations(vector<int>& nums, int k)
{
    int size = nums.size();
    sort(nums.begin(), nums.end(), cmp);    // 第一步
    for (int i = 0; i < nums.size(); i++) { // 第二步
        if (nums[i] < 0 && k > 0) {
            nums[i] = -nums[i];
            k--;
        }
    }
    if (k % 2 == 1) nums[size - 1] = -nums[size - 1]; // 第三步

    int result = 0;
    for (int a : nums)
        result += a;        // 第四步
    return result;
}

LC134. 加油站

只能想到暴力解法，这里就贴Carl哥的思路和代码：

首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈，说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。每个加油站的剩余量rest[i]为gas[i] - cost[i]。

i从0开始累加rest[i]，和记为curSum，一旦curSum小于零，说明[0, i]区间都不能作为起始位置，因为这个区间选择任何一个位置作为起点，到i这里都会断油，那么起始位置从i+1算起，再从0计算curSum。

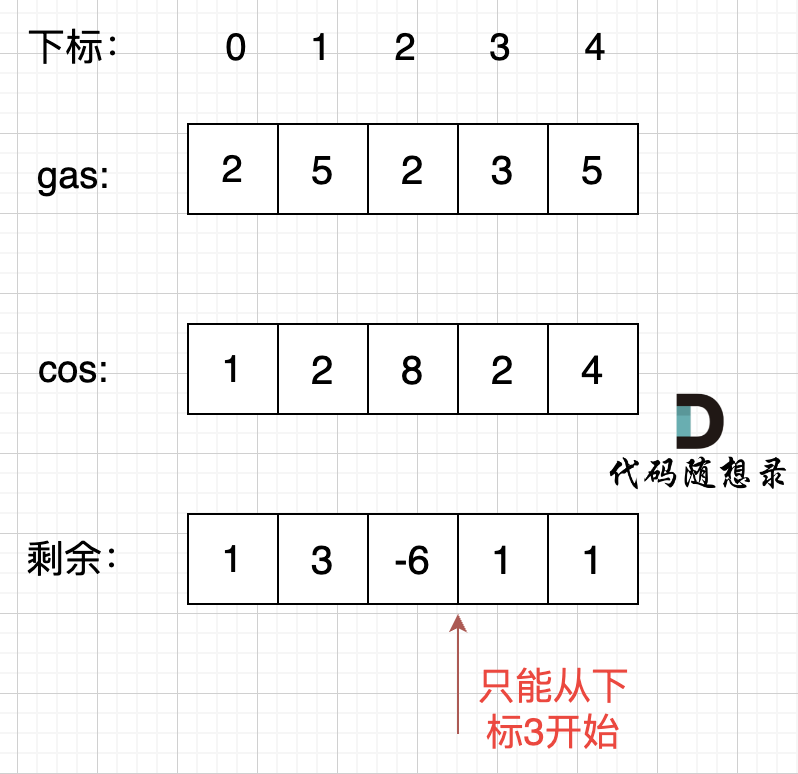
那么为什么一旦[0，i] 区间和为负数，起始位置就可以是i+1呢，i+1后面就不会出现更大的负数？

如果出现更大的负数，就是更新i，那么起始位置又变成新的i+1了。

那有没有可能 [0，i] 区间 选某一个作为起点，累加到 i这里 curSum是不会小于零呢？

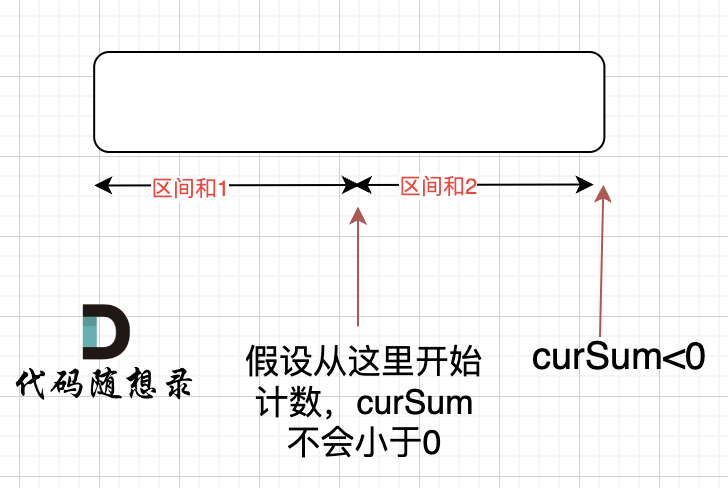
如果 curSum<0 说明 区间和1 + 区间和2 < 0， 那么 假设从上图中的位置开始计数curSum不会小于0的话，就是 区间和2>0。

区间和1 + 区间和2 < 0 同时 区间和2>0，只能说明区间和1 < 0， 那么就会从假设的箭头初就开始从新选择其实位置了。

那么局部最优：当前累加rest[i]的和curSum一旦小于0，起始位置至少要是i+1，因为从i之前开始一定不行。全局最优：找到可以跑一圈的起始位置。

int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
    int curSum = 0;
    int totalSum = 0;
    int start = 0;
    for (int i = 0; i < gas.size(); i++) {
        curSum += gas[i] - cost[i];
        totalSum += gas[i] - cost[i];
        if (curSum < 0) {   // 当前累加rest[i]和 curSum一旦小于0
            start = i + 1;  // 起始位置更新为i+1
            curSum = 0;     // curSum从0开始
        }
    }
    if (totalSum < 0) return -1; // 说明怎么走都不可能跑一圈了
    return start;
}

LC135. 分发糖果

着实没想到可以：根据左右规则，从左右各遍历一次，去最大值。

这里采用的是暴力解法O(n^2)，力扣上会报“超出时间限制”。

int candy(vector<int>& ratings)
{
    vector<int> alloc(ratings.size(), 0);
    alloc[0] = 1;
    for (int i = 1; i < ratings.size(); ++i)
    {
        if (ratings[i] <= ratings[i - 1])
        {
            alloc[i] = 1;
        }
        else if (ratings[i] > ratings[i - 1])
        {
            alloc[i] = alloc[i - 1] + 1;
        }

        if (alloc[i] == 1 && alloc[i - 1] == 1 && ratings[i] != ratings[i - 1])
        {
            int index = i;
            int temp = alloc[i - 1];
            while (index >= 1 && alloc[index - 1] == alloc[index] && ratings[index - 1] != ratings[index])
            {
                ++alloc[index - 1];
                --index;
            }
        }
    }

    int sum = 0;
    for (int i : alloc)
        sum += i;
    return sum;
}