今天就是打家劫舍的一天,这个系列不算难,大家可以一口气拿下。
198.打家劫舍
视频讲解:https://www.bilibili.com/video/BV1Te411N7SX
https://programmercarl.com/0198.%E6%89%93%E5%AE%B6%E5%8A%AB%E8%88%8D.html
Tips:
大家如果刚接触这样的题目,会有点困惑,当前的状态我是偷还是不偷呢?
仔细一想,当前房屋偷与不偷取决于 前一个房屋和前两个房屋是否被偷了。
所以这里就更感觉到,当前状态和前面状态会有一种依赖关系,那么这种依赖关系都是动规的递推公式。
当然以上是大概思路,打家劫舍是dp解决的经典问题,接下来我们来动规五部曲分析如下:
- 确定dp数组(dp table)以及下标的含义
dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]。
- 确定递推公式
决定dp[i]的因素就是第i房间偷还是不偷。
如果偷第i房间,那么dp[i] = dp[i - 2] + nums[i] ,即:第i-1房一定是不考虑的,找出 下标i-2(包括i-2)以内的房屋,最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。
如果不偷第i房间,那么dp[i] = dp[i - 1],即考 虑i-1房,(注意这里是考虑,并不是一定要偷i-1房,这是很多同学容易混淆的点)
然后dp[i]取最大值,即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
- dp数组如何初始化
从递推公式dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);可以看出,递推公式的基础就是dp[0] 和 dp[1]
从dp[i]的定义上来讲,dp[0] 一定是 nums[0],dp[1]就是nums[0]和nums[1]的最大值即:dp[1] = max(nums[0], nums[1]);
我的题解:
class Solution {
public:
int rob(vector<int>& nums) {
if(nums.size()==1){
return nums[0];
}
vector<int> dp(nums.size(), 0);
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
for(int i = 2; i <nums.size(); i++){
dp[i] = max(dp[i-2] + nums[i], dp[i-1]);
}
return dp[nums.size()-1];
}
};213.打家劫舍II
视频讲解:https://www.bilibili.com/video/BV1oM411B7xq
https://programmercarl.com/0213.%E6%89%93%E5%AE%B6%E5%8A%AB%E8%88%8DII.html
Tips:将一个大问题拆分为两个子问题:
这道题目和198.打家劫舍 (opens new window)是差不多的,唯一区别就是成环了。
对于一个数组,成环的话主要有如下三种情况:
- 情况一:考虑不包含首尾元素
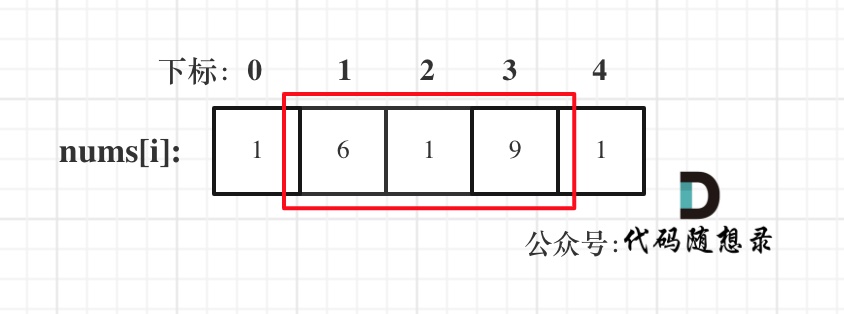
- 情况二:考虑包含首元素,不包含尾元素
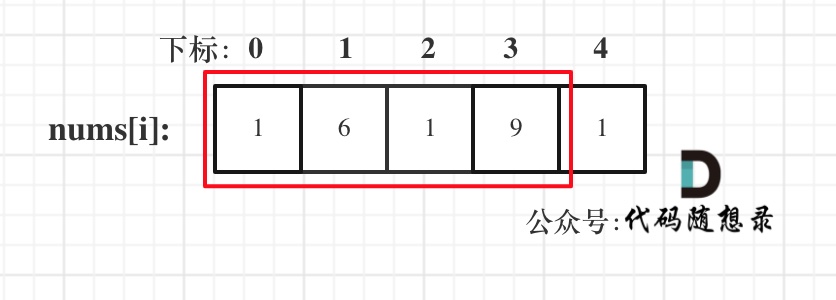
- 情况三:考虑包含尾元素,不包含首元素
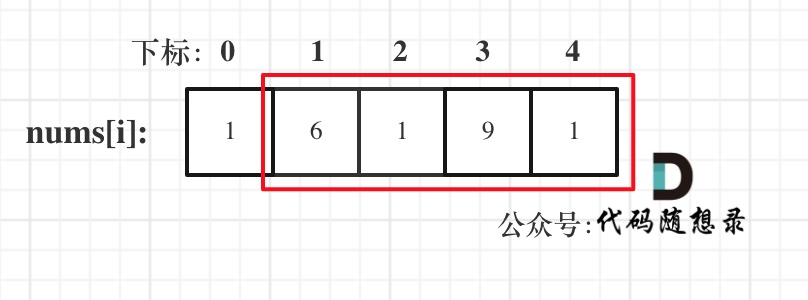
注意我这里用的是"考虑",例如情况三,虽然是考虑包含尾元素,但不一定要选尾部元素! 对于情况三,取nums[1] 和 nums[3]就是最大的。
而情况二 和 情况三 都包含了情况一了,所以只考虑情况二和情况三就可以了。
分析到这里,本题其实比较简单了。 剩下的和198.打家劫舍 (opens new window)就是一样的了。
我的题解:
class Solution {
public:
int rob(vector<int>& nums) {
if(nums.size() == 1){
return nums[0];
}
int haveFirst = robRange(nums,0,nums.size()-2);
int haveLast = robRange(nums,1,nums.size() -1);
return max(haveFirst,haveLast);
}
int robRange(vector<int>& nums, int start, int end){
if(end == start) return nums[start];
vector<int> dp(nums.size(),0);
dp[start] = nums[start];
dp[start+1] = max(nums[start], nums[start+1]);
for(int i=start+2;i<=end;i++){
dp[i] = max(dp[i-1], dp[i-2] + nums[i]);
}
return dp[end];
}
};337.打家劫舍III
视频讲解:https://www.bilibili.com/video/BV1H24y1Q7sY
https://programmercarl.com/0337.%E6%89%93%E5%AE%B6%E5%8A%AB%E8%88%8DIII.html
Tips:
动态规划其实就是使用状态转移容器来记录状态的变化,这里可以使用一个长度为2的数组,记录当前节点偷与不偷所得到的的最大金钱。
这道题目算是树形dp的入门题目,因为是在树上进行状态转移,我们在讲解二叉树的时候说过递归三部曲,那么下面我以递归三部曲为框架,其中融合动规五部曲的内容来进行讲解。
- 确定递归函数的参数和返回值
这里我们要求一个节点 偷与不偷的两个状态所得到的金钱,那么返回值就是一个长度为2的数组。
参数为当前节点,代码如下:
vector<int> robTree(TreeNode* cur) {其实这里的返回数组就是dp数组。
所以dp数组(dp table)以及下标的含义:下标为0记录不偷该节点所得到的的最大金钱,下标为1记录偷该节点所得到的的最大金钱。
所以本题dp数组就是一个长度为2的数组!
那么有同学可能疑惑,长度为2的数组怎么标记树中每个节点的状态呢?
别忘了在递归的过程中,系统栈会保存每一层递归的参数。
如果还不理解的话,就接着往下看,看到代码就理解了哈。
- 确定终止条件
在遍历的过程中,如果遇到空节点的话,很明显,无论偷还是不偷都是0,所以就返回
if (cur == NULL) return vector<int>{0, 0};这也相当于dp数组的初始化
- 确定遍历顺序
首先明确的是使用后序遍历。 因为要通过递归函数的返回值来做下一步计算。
通过递归左节点,得到左节点偷与不偷的金钱。
通过递归右节点,得到右节点偷与不偷的金钱。
代码如下:
// 下标0:不偷,下标1:偷
vector<int> left = robTree(cur->left); // 左
vector<int> right = robTree(cur->right); // 右
// 中- 确定单层递归的逻辑
如果是偷当前节点,那么左右孩子就不能偷,val1 = cur->val + left[0] + right[0]; (如果对下标含义不理解就再回顾一下dp数组的含义)
如果不偷当前节点,那么左右孩子就可以偷,至于到底偷不偷一定是选一个最大的,所以:val2 = max(left[0], left[1]) + max(right[0], right[1]);
最后当前节点的状态就是{val2, val1}; 即:{不偷当前节点得到的最大金钱,偷当前节点得到的最大金钱}
代码如下:
vector<int> left = robTree(cur->left); // 左
vector<int> right = robTree(cur->right); // 右
// 偷cur
int val1 = cur->val + left[0] + right[0];
// 不偷cur
int val2 = max(left[0], left[1]) + max(right[0], right[1]);
return {val2, val1};我的题解:
1. 树形DP
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
// 0: 不偷当前节点 1: 偷当前节点
vector<int> traversal(TreeNode* node){
if(node == NULL){
return vector<int>{0, 0};
}
vector<int> left = traversal(node->left);
vector<int> right = traversal(node->right);
// 偷的话
int val1 = node->val + left[0] + right[0];
// 不偷的话
int val2 = max(left[0],left[1]) + max(right[0],right[1]);
return {val2, val1};
}
int rob(TreeNode* root) {
vector<int> result = traversal(root);
return max(result[0], result[1]);
}
};2. 记忆化递归
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
unordered_map<TreeNode*, int> umap;
int rob(TreeNode* root) {
if(root == NULL) return 0;
if(root->left == NULL && root->right == NULL) return root->val;
if(umap[root]) return umap[root];
// rob current node
int rob1 = root->val;
if(root->left) rob1 += rob(root->left->left) + rob(root->left->right);
if(root->right) rob1 += rob(root->right->left) + rob(root->right->right);
int rob2 = rob(root->left) + rob(root->right);
umap[root] = max(rob1,rob2);
return max(rob1,rob2);
}
};