排序算法整理
常见考点
- 将一个乱掉的字符串排回有序(以交换为基本操作)的最少操作,就是冒泡排序。
- 排序算法的稳定性
- 排序算法的时间复杂度
排序算法的稳定性
稳定性是指排序前两个元素a1 = a2,a1在前。排序过后,倘若a1始终在前,则算法是稳定的,否则是不稳定的。
稳定的
[冒泡排序](#3 - 冒泡排序)、插入排序、[归并排序](#3 - 归并排序)、基数排序
不稳定的
堆排序、[快速排序](#3 - 快速排序)、希尔排序、[选择排序](#3 - 选择排序)
各个算法细锁
冒泡排序
基本思路:双重循环遍历数组,交换两个相邻的逆序的数字。时间复杂度一般 - \(O(n^2)\),最坏 - \(O(n^2)\),最好\(O(n)\)。
代码
for(int i = 1; i <= n; i ++)
{
for(int j = 1; j <= n - i; j ++)
{
if(a[j] > a[j + 1])
swap(a[j], a[j + 1]);
}
}
都说最优复杂度是O(N),但显然这个程序怎么看都是\(O(n^2)\),实际上\(O(n)\)是优化过的。考试的时候记住就行。
选择排序
基本思路:遍历一遍数组 i in (1, n + 1),从 i 数开始遍历到后面,寻找最小的比它小的数,与它交换。
无论如何都是\(O(n^2)\)。
代码
for(int i = 1; i < n; i ++)
{
int min = i;
for(j = i + 1; j <= n; j ++)
{
if(a[min] > a[j])
min = j;
swap(a[i], a[min]);
}
}
归并排序
分治思想,将数组中所有的数递归分为两个一组
网上讲的挺好的归并排序MergeSort(通俗易懂_kevinmeanscool的博客-CSDN
这个算法还能用来求逆序对,所以在复赛中也挺重要 虽然现在一般复赛不会考,只要在else后面(代码)加一句ans += mid - i +1,但我不知道原理。
代码
void merge_sort(int a[], int l, int r){
if(l >= r)
return;
int mid = l + r >> 1;
merge_sort(a, l, mid);
merge_sort(a, mid + 1, r);
int k = 0;
int i = l;
int j = mid + 1;
while(i <= mid && j <= r){
if(a[i] <= a[j])
f[k ++] = a[i ++];
else
f[k ++] = a[j ++];
}
while(i <= mid) f[k ++] = a[i ++];
while(j <= r) f[k ++] = a[j ++];
for(i = l, j = 0; i <= r; i ++, j ++){
a[i] = f[j];
}
}
快速排序
基本思路:找一个基准数,先由i从左边出发,找到一个小于,j再从右边出发,找一个小于基准数的数。分开区间,重复此操作。时间复杂度平均\(O(nlon_n)\),最优也是\(O(nlon_n)\),最差\(O(n^2)\)。
代码
void qsort(int l, int r)
{
int mid = a[l + r >> 1];
int i = l, j = r;
do{
while(a[i] < mid) i ++;
while(a[j] > mid) j --;
if(i <= j)
{
swap(a[i], a[j]);
i ++;
j --;
}
}while(i <= j);
if(l < j) qsort(l, j);
if(i < r) qsort(i, r);
}
int main()
{
qsort(1, n);
}
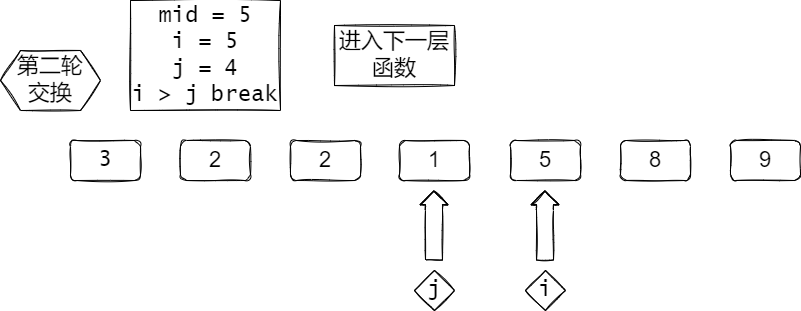
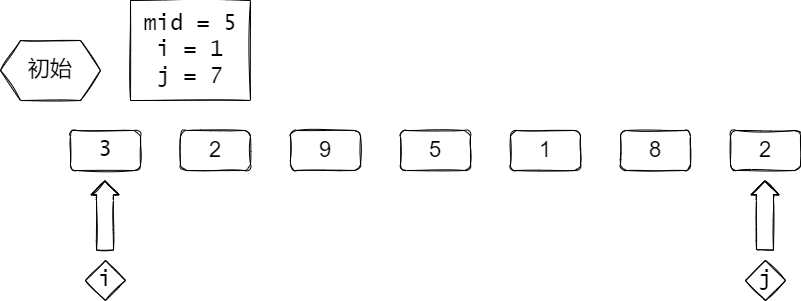
根据代码图解
(如果加载不出来请刷新,因为图放在Github):
数组:[3, 2, 9, 5, 1, 8, 2]
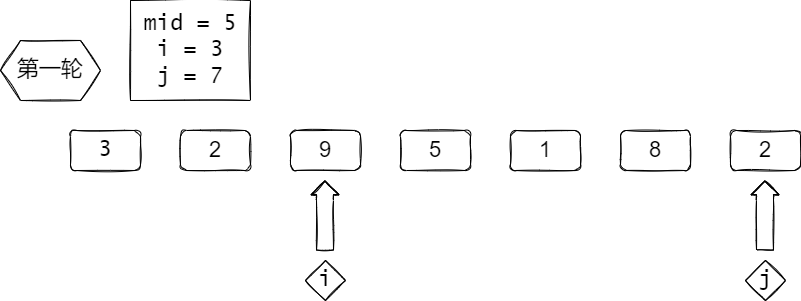
找到了
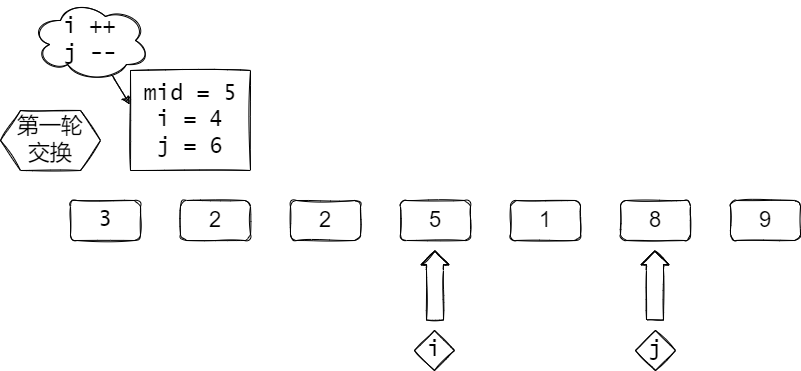
交换,注意i ++, j -- 不然会死循环
i 不再动了,因为a[i] = mid
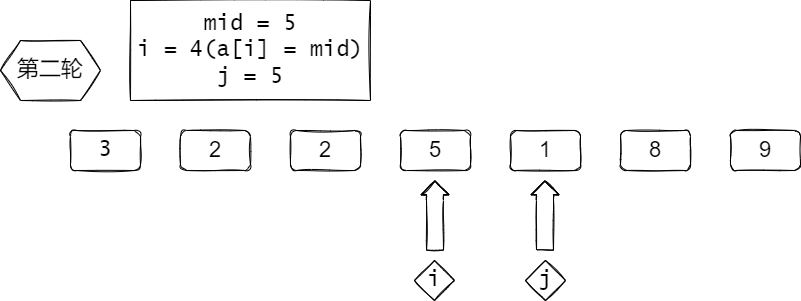
这里没写 i ++, j --