102. 二叉树的层序遍历
文章:代码随想录 (programmercarl.com)
视频:讲透二叉树的层序遍历 | 广度优先搜索 | LeetCode:102.二叉树的层序遍历_哔哩哔哩_bilibili
思路:
层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。
需要借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
而这种层序遍历方式就是图论中的广度优先遍历,只不过我们应用在二叉树上。
使用队列实现二叉树广度优先遍历,动画如下:

class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
//迭代法
if (root != NULL)
{
que.push(root);
}
//定义存放结果的二维数组
vector<vector<int>> result;
//队列为空时,循环结束
while (!que.empty())
{
//获取队列长度——每一层的元素个数
int size = que.size();
//定义一维数组,存放每一层的元素
vector<int> vec;
//第二层循环结束的条件:每一层元素全部弹出时,本层循环结束
while (size--)
{
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
//如果弹出元素有子结点时,将子节点加入队列
if (node->left != NULL)
{
que.push(node->left);
}
if (node->right != NULL)
{
que.push(node->right);
}
}
//循环结束,将一维数组存入二维数组result中
result.push_back(vec);
}
return result;
}
};
107. 二叉树的层序遍历 II
思路:
相对于102.二叉树的层序遍历,就是最后把result数组反转一下就可以了。
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL)
{
que.push(root);
}
vector<vector<int>> result;
while (!que.empty())
{
int size = que.size();
vector<int> vec;
while (size--)
{
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if (node->left != NULL)
{
que.push(node->left);
}
if (node->right != NULL)
{
que.push(node->right);
}
}
result.push_back(vec);
}
reverse(result.begin(), result.end());
return result;
}
};
199. 二叉树的右视图
思路:
层序遍历的时候,判断是否遍历到单层的最后面的元素,如果是,就放进result数组中,随后返回result就可以了。
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL)
{
que.push(root);
}
vector<int> result;
while (!que.empty())
{
int size = que.size();
while (size--)
{
TreeNode* node = que.front();
que.pop();
if (size == 0)
{
result.push_back(node->val);
}
if (node->left != NULL)
{
que.push(node->left);
}
if (node->right != NULL)
{
que.push(node->right);
}
}
}
return result;
}
};
637. 二叉树的层平均值
思路:
本题就是层序遍历的时候把一层求个总和在取一个均值
class Solution {
public:
vector<double> averageOfLevels(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL)
{
que.push(root);
}
vector<double> result;
while (!que.empty())
{
int size = que.size();
int size_pro = size;
double sum = 0;
while (size--)
{
TreeNode* node = que.front();
que.pop();
sum += node->val;
if (node->left != NULL)
{
que.push(node->left);
}
if (node->right != NULL)
{
que.push(node->right);
}
}
result.push_back(sum / size_pro);
}
return result;
}
};
429. N 叉树的层序遍历
思路:
这道题依旧是模板题,只不过一个节点有多个孩子了
二叉树的孩子用node->left,node->right表示
N叉树的孩子用node->children[i]表示
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
queue<Node*> que;
if (root != NULL)
{
que.push(root);
}
vector<vector<int>> result;
while (!que.empty())
{
int size = que.size();
vector<int> vec;
while (size--)
{
Node* node = que.front();
que.pop();
vec.push_back(node->val);
//N叉树和二叉树的层序遍历只在最后将子节点插入队列中有差异
for (int i = 0; i < node->children.size(); i++)
{
if (node->children[i] != NULL)
{
que.push(node->children[i]);
}
}
}
result.push_back(vec);
}
return result;
}
};
515. 在每个树行中找最大值
思路:
层序遍历,取每一层的最大值
class Solution {
public:
vector<int> largestValues(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL)
{
que.push(root);
}
vector<int> result;
while (!que.empty())
{
int size = que.size();
int max = INT_MIN;
while (size--)
{
TreeNode* node = que.front();
que.pop();
if (node->val > max)
{
max = node->val;
}
if (node->left != NULL)
{
que.push(node->left);
}
if (node->right != NULL)
{
que.push(node->right);
}
}
result.push_back(max);
}
return result;
}
};
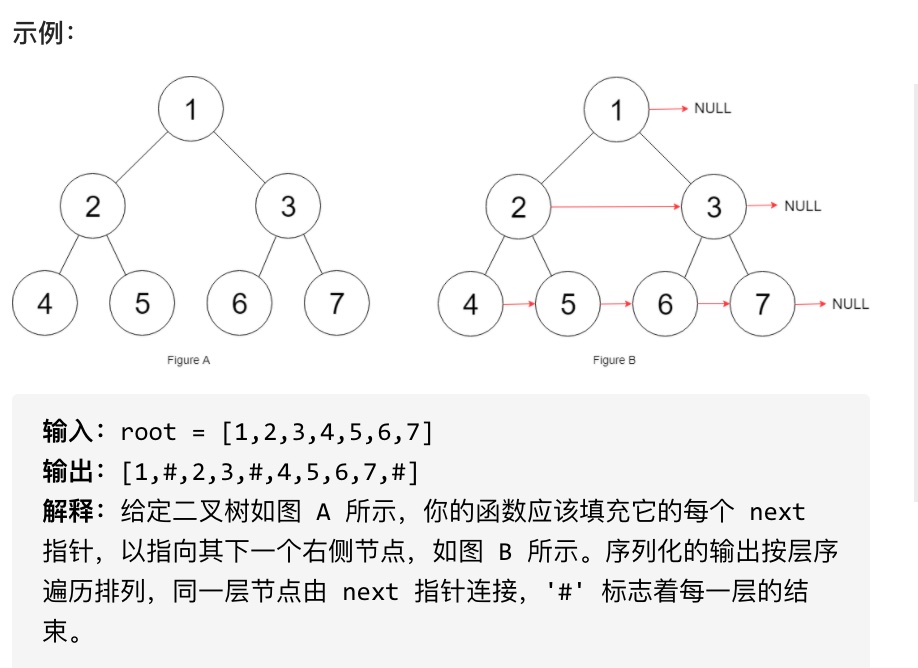
116. 填充每个节点的下一个右侧节点指针
思路:
本题依然是层序遍历,只不过在单层遍历的时候记录一下本层的头部节点,然后在遍历的时候让前一个节点指向本节点就可以了
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if (root != NULL)
{
que.push(root);
}
while (!que.empty())
{
int size = que.size();
Node* nodePre;//前驱节点
Node* node;//当前结点
for (int i = 0; i < size; i++)
{
if (i == 0) //位于本层第一个元素时,头结点既是当前结点,也是前驱节点
{
nodePre = que.front();
que.pop();
node = nodePre;
}
else //不是本层头结点时
{
node = que.front();
que.pop();
nodePre->next = node; //前驱节点指向当前结点
nodePre = nodePre->next; //前驱节点后移一位
}
if (node->left != NULL)
{
que.push(node->left);
}
if (node->right != NULL)
{
que.push(node->right);
}
}
nodePre->next = NULL; //本层最后一个元素的指针指向NULL
}
return root;
}
};
117. 填充每个节点的下一个右侧节点指针 II
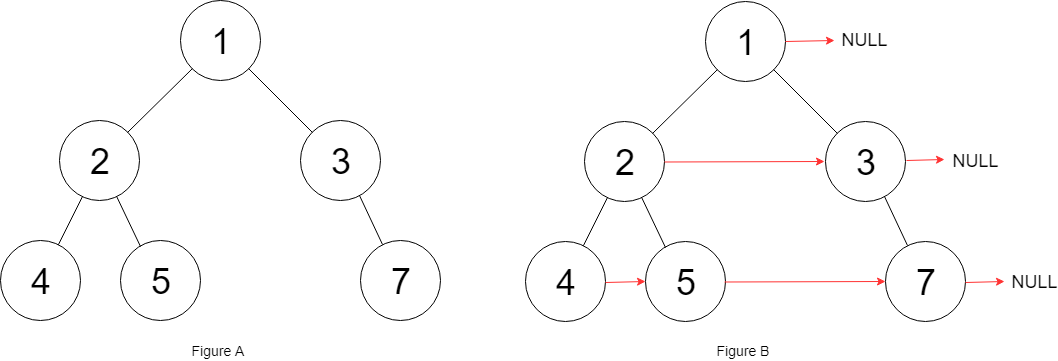
思路:
这道题目说是二叉树,但116题目说是完整二叉树,其实没有任何差别,一样的代码一样的逻辑一样的味道
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if (root != NULL)
{
que.push(root);
}
while (!que.empty())
{
int size = que.size();
Node* nodePre;
Node* node;
for (int i = 0; i < size; i++)
{
if (i == 0)
{
nodePre = que.front();
que.pop();
node = nodePre;
}
else
{
node = que.front();
que.pop();
nodePre->next = node;
nodePre = nodePre->next;
}
if (node->left != NULL)
{
que.push(node->left);
}
if (node->right != NULL)
{
que.push(node->right);
}
}
nodePre->next = NULL;
}
return root;
}
};
104. 二叉树的最大深度
class Solution {
public:
int maxDepth(TreeNode* root) {
if (root == NULL)
{
return 0;
}
queue<TreeNode*> que;
que.push(root);
int depth = 0;
while (!que.empty())
{
int size = que.size();
while (size--)
{
TreeNode* node = que.front();
que.pop();
if (node->left != NULL)
{
que.push(node->left);
}
if (node->right != NULL)
{
que.push(node->right);
}
}
depth++;
}
return depth;
}
};
111. 二叉树的最小深度
思路:
需要注意的是,只有当左右孩子都为空的时候,才说明遍历的最低点了。如果其中一个孩子为空则不是最低点
class Solution {
public:
int minDepth(TreeNode* root) {
if (root == NULL)
{
return 0;
}
queue<TreeNode*> que;
que.push(root);
int minDepth = 0;
while (!que.empty())
{
int size = que.size();
minDepth++;
while (size--)
{
TreeNode* node = que.front();
que.pop();
if (node->left != NULL)
{
que.push(node->left);
}
if (node->right != NULL)
{
que.push(node->right);
}
if (node->left == NULL && node->right == NULL)
{
return minDepth;
}
}
}
return minDepth;
}
};
226. 翻转二叉树
文章:代码随想录 (programmercarl.com)
视频:听说一位巨佬面Google被拒了,因为没写出翻转二叉树 | LeetCode:226.翻转二叉树_哔哩哔哩_bilibili
思路:
如果要从整个树来看,翻转还真的挺复杂,整个树以中间分割线进行翻转,如图:
注意只要把每一个节点的左右孩子翻转一下,就可以达到整体翻转的效果
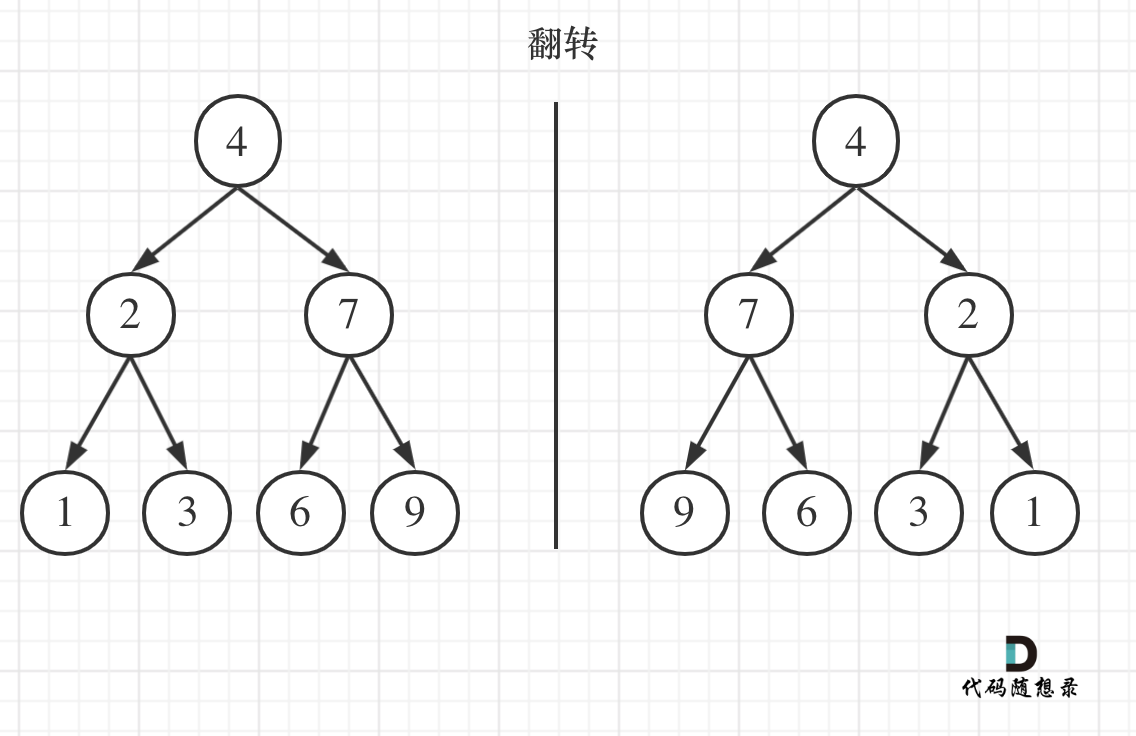
可以发现想要翻转它,其实就把每一个节点的左右孩子交换一下就可以了。
遍历的过程中去翻转每一个节点的左右孩子就可以达到整体翻转的效果。
注意只要把每一个节点的左右孩子翻转一下,就可以达到整体翻转的效果
这道题目使用前序遍历和后序遍历都可以,唯独中序遍历不方便,因为中序遍历会把某些节点的左右孩子翻转了两次!建议拿纸画一画,就理解了
那么层序遍历可以不可以呢?依然可以的!只要把每一个节点的左右孩子翻转一下的遍历方式都是可以的!
我们下文以前序遍历为例,通过动画来看一下翻转的过程:

class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
//root不是整个二叉树的根节点,而是当前结点
if (root == NULL)
{
return NULL;
}
swap(root->left, root->right);
invertTree(root->left);
invertTree(root->right);
return root;
}
};
101. 对称二叉树
文章:代码随想录 (programmercarl.com)
视频:新学期要从学习二叉树开始! | LeetCode:101. 对称二叉树_哔哩哔哩_bilibili
思路:
首先想清楚,判断对称二叉树要比较的是哪两个节点,要比较的可不是左右节点!
对于二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,理解这一点就知道了其实我们要比较的是两个树(这两个树是根节点的左右子树),所以在递归遍历的过程中,也是要同时遍历两棵树。
那么如何比较呢?
比较的是两个子树的里侧和外侧的元素是否相等。如图所示:
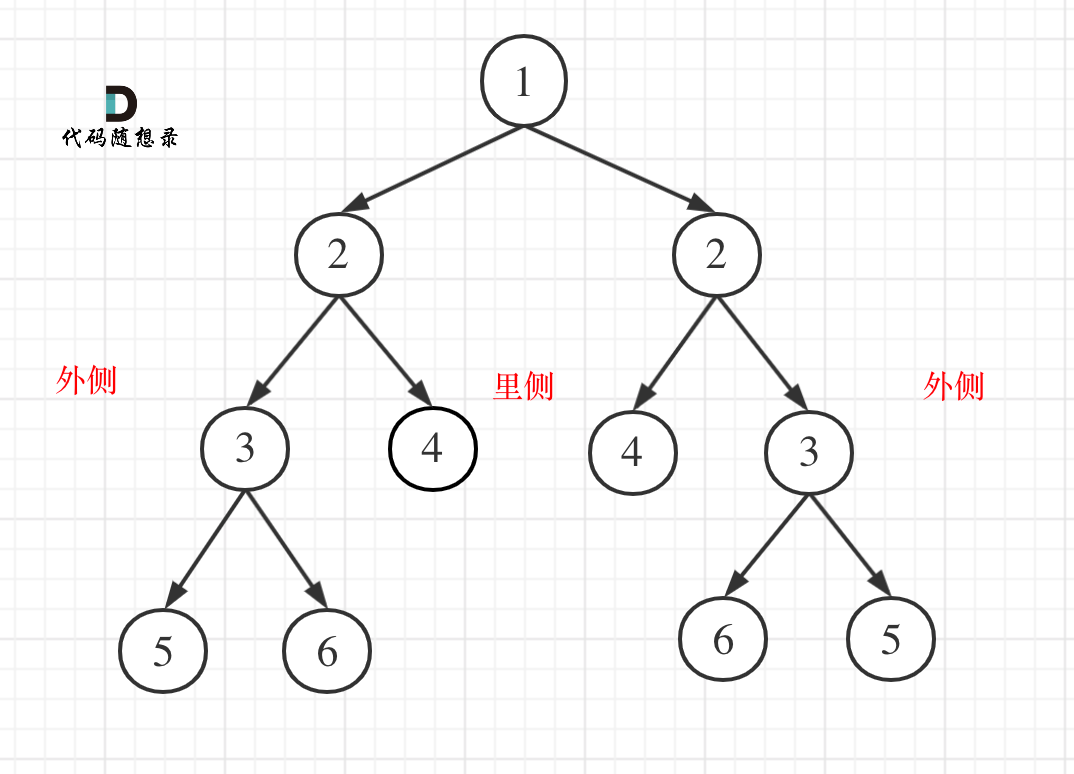
那么遍历的顺序应该是什么样的呢?
本题遍历只能是“后序遍历”,因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。
class Solution {
public:
bool compare(TreeNode* left, TreeNode* right)
{
if (left == NULL && right != NULL)
{
return false;
}
else if (left != NULL && right == NULL){
return false;
}
else if (left == NULL && right == NULL) {
return true;
}
else if (left->val != right->val) {
return false;
}
else {
bool outside = compare(left->left, right->right);
bool inside = compare(left->right, right->left);
return outside && inside;
}
}
bool isSymmetric(TreeNode* root) {
if (root == NULL)
{
return true;
}
return compare(root->left, root->right);
}
};