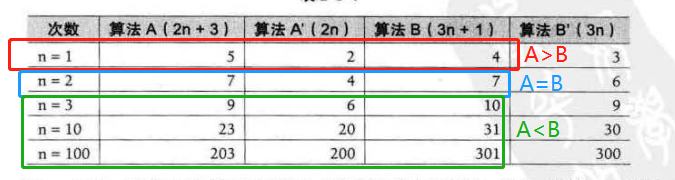
- 【算法|习题总结】算法分析与计算复杂性在线测试Ⅰ
目录前言题目一内容参考Demo题目二内容参考Demo题目三内容参考Demo题目四......
- 什么是数据结构
数据结构是一门研究非数值计算的程序设计问题中的操作对象,以及它们之间的关系和操作等相关问题的学科。什么是数据数据是描述客观事物的符号,是计算机中可以操作的对象,......
- 【MATLAB优化算法】遗传算法理论部分
遗传算法引言遗传算法(GeneticAlgorithm,GA)是模拟生物在自然境中的遗传和进化的过程而形成的自适应全局优化的搜索算法。它借用了生物遗传学的观点,通过自然选择、遗传和变......
- Pytorch的cross_entropy为什么等于log_softmax加nll_loss
首先我们要知道nll_loss是怎么算的,看下面的代码label1=torch.tensor([0,3])pred1=torch.tensor([[0.2,0.7,0.8,0.1],[0.1,0.3,0.5,0.7]])lo......
- 代码随想录算法训练营第15天
今日刷题3道:层序遍历, 226.翻转二叉树,101.对称二叉树2● 层序遍历10题目链接/文章讲解/视频讲解:https://programmercarl.com/0102.%E4%BA%8C%E5%8F%89%E6%A......
- m基于OFDM系统,对比SC算法,Minn算法,PARK算法同步性能matlab仿真分析
1.算法描述 OFDM系统下对比SC算法,Minn算法,PARK算法同步性能matlab仿真分析。OFDM系统中的定时估计和频率频率算法——时频联合估计的SC算法,由Schmidl和Cox......
- m基于OFDM系统,对比SC算法,Minn算法,PARK算法同步性能matlab仿真分析
1.算法描述OFDM系统下对比SC算法,Minn算法,PARK算法同步性能matlab仿真分析。OFDM系统中的定时估计和频率频率算法——时频联合估计的SC算法,由Schmidl和Cox提出,是一种基于训......
- 为什么我放弃Java,选择Kotlin(靠特灵)?
今天查了一下,竟然发现Oracle的JDK听说是收费了。也就是说,你要用于生产环境的话,Oracle一旦查到你,你就要交钱的。我本身是个穷光蛋,哪还有钱交给Oracle。为了避免繁琐的法律制......
- 为什么使用消息队列?
理解:但是比较核心的有3个:解耦、异步、削峰解耦:A把数据放到MQ中,BCD需要就取,不需要就不取。A不用管BCD的需求异步:BCD会把数据存入对应的MQ,A可以直接取,可达到异步缩减时......
- Linux内核为什么会发生soft lockup?【转】
转自:https://blog.csdn.net/21cnbao/article/details/108250786提到softlockup,大家都不会陌生:BUG: soft lockup - CPU#3 stuck for 23s! [kworker/3:0:32]......