代码随想录算法训练营Day18|513. 找树左下角的值、112. 路径总和、106. 从中序与后序遍历序列构造二叉树
513. 找树左下角的值
假设二叉树中至少有一个节点。因此排除了根节点为空的情况,我们在层序遍历插入根节点是不用考虑异常情况。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
queue<TreeNode*> que;
// 题目要求二叉树根节点不为空,不用讨论
que.push(root);
int res;
while (!que.empty()) {
vector<int> row;
int size = que.size();
while (size--) {
TreeNode* node = que.front();
que.pop();
row.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
res = row.front();
}
return res;
}
};
这里再进行优化,不需要用容器保存整行的元素,再每层遍历时刷新第一个元素的值即可,这里需要我们调整遍历手段用for循环代替while循环方便获取首位元素的值,完整代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
queue<TreeNode*> que;
// 题目要求二叉树根节点不为空,不用讨论
que.push(root);
int res;
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
if (i == 0) res = node->val;
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return res;
}
};
112. 路径总和
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
return getPathSum(root, 0, targetSum);
}
bool getPathSum(TreeNode* node, int sum, int targetSum) {
if (node == NULL) return false;
sum += node->val;
if (node->left == NULL && node->right == NULL) {
return targetSum == sum ? true : false;
}
bool left = getPathSum(node->left, sum, targetSum);
bool right = getPathSum(node->right, sum, targetSum);
return (left || right);
}
};
这里因为需要比较目标值yatgetSum和累加的路径和,要一直再函数传递targetSUm这个固定参数,造成了额外的开销。不要去累加然后判断是否等于目标和,那么代码比较麻烦,可以用递减,让计数器count初始为目标和,然后每次减去遍历路径节点上的数值。当判断为叶子节点时,判断递减的目标和是否归零来判断路径和是否相等:
if (node->left == NULL && node->right == NULL) {
return targetSum == 0 ? true : false;
}
完整代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
return getPathSum(root, targetSum);
}
bool getPathSum(TreeNode* node, int targetSum) {
if (node == NULL) return false;
targetSum -= node->val;
if (node->left == NULL && node->right == NULL) {
return targetSum == 0 ? true : false;
}
bool left = getPathSum(node->left, targetSum);
bool right = getPathSum(node->right, targetSum);
return (left || right);
}
};
另外上述代码的终止条件设置为if (node == NULL) return false;其实含义不是很清晰,虽然可以避免对左右孩子节点是否为空进行讨论,但真正的终止条件其实是if (node->left == NULL && node->right == NULL)。如果要去掉节点为空的条件,由于判断左右孩子节点可以串行判断,可以考虑在遍历孩子节点时再添加是否为空的判断:
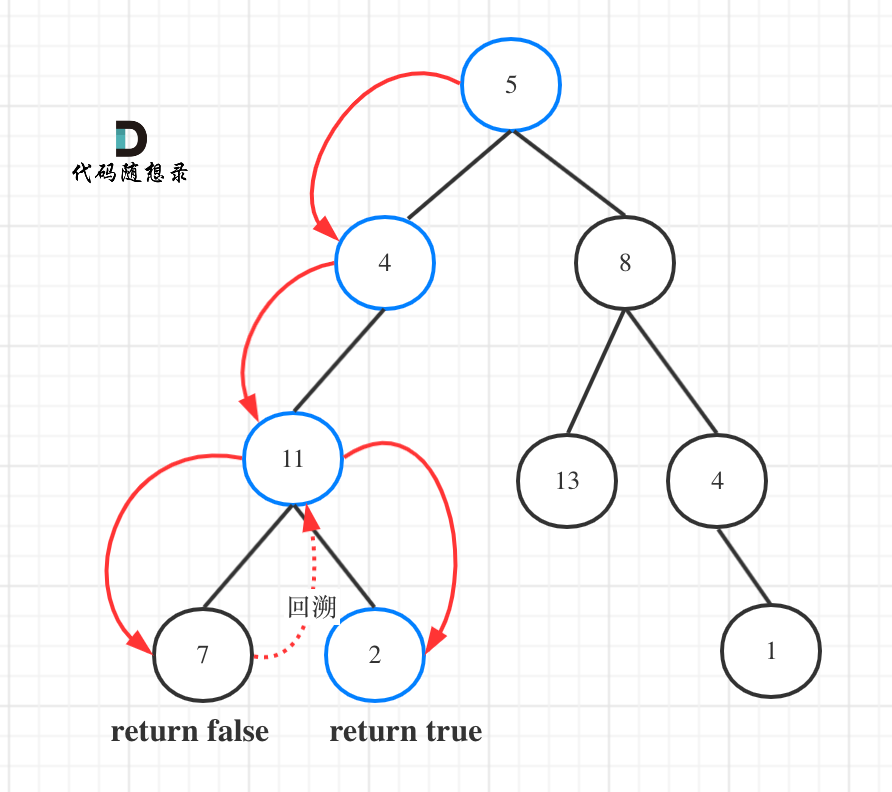
这样会引入一个回溯问题,就是进入递归函数时不能立即递减targetSum,只有在孩子节点不为空的情况下,才能对目标值进行修改,并且完成左孩子判断后需要还原目标值来进行右孩子节点的判断,一次来体现回溯的思想:
if (node->left) {
targetSum -= node->val;
return getPathSum(node->left, targetSum);
targetSum += node->val;
}
if (node->right) {
targetSum -= node->val;
return getPathSum(node->right, targetSum);
targetSum += node->val;
}
重点在于左/右孩子节点可以串行判断。之前的方法不判断是因为他默认一定会传入左/右孩子节点,所以在进行分支前统一递减并且结果共用,避免了递归的多次操作,完整代码如下:
if (node->left)
if (getPathSum(node->left, targetSum)) return true;
if (node->right)
if (getPathSum(node->right, targetSum)) return true;
完整代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if (root == NULL) return false;
return getPathSum(root, targetSum);
}
bool getPathSum(TreeNode* node, int targetSum) {
targetSum -= node->val;
if (node->left == NULL && node->right == NULL) {
return targetSum == 0 ? true : false;
}
if (node->left)
if (getPathSum(node->left, targetSum)) return true;
if (node->right)
if (getPathSum(node->right, targetSum)) return true;
return false;
}
};
106. 从中序与后序遍历序列构造二叉树
注意本题题目要求:
-
inorder和postorder都由 不同 的值组成:意味着可以通过值唯一确定不同的节点
-
inorder保证是树的中序遍历/postorder保证是树的后序遍历确保输入内容正确,我们也可以选择对输入内容进行异常处理,判断其中任何一个数组的长度即可:
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
本题核心在于根据后续遍历末尾节点确认中间节点,以此分基础进行分割。
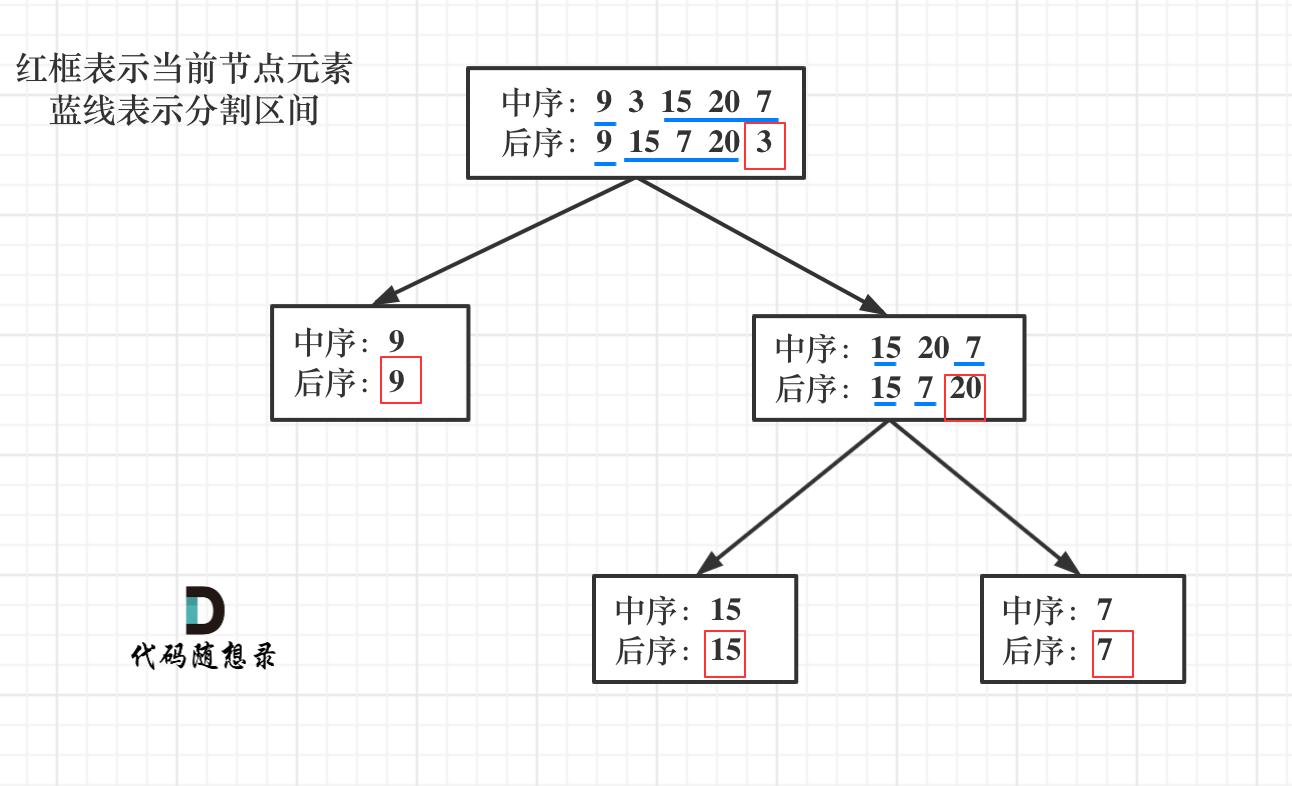
这里涉及到数组的分割,我们初始化数组时分割区间为左闭右开。
vector<int> test = {1, 2, 3};
// 如果需要截取前2个元素,末位指针需要指在第三个元素3上
vetor<int> delimiter(test.begin(), test.begin() + 2);
// delemiter为{1, 2}
另外虽然递归函数的终结条件为postorder.size() == 0即返回空节点,我们也可以剪枝一下遍历流程:当postorder.size() == 1时,我们直接返回当前节点,因为前序/后序数组长度相等,此时已经遍历到叶子结点,没有分割数组的必要了:
if (postorder.size() == 1) return root;
另外还有个细节是后序数组切分前需要重置数组长度,来去掉末尾的中间节点,它是不需要递归到左右孩子节点中去的:
postorder.resize(postorder.size() - 1);
完整代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
return traversal(inorder, postorder);
}
TreeNode* traversal(vector<int> inorder, vector<int> postorder) {
// 递归的判断条件都使用后序数组,因为他是分割的起点
if (postorder.size() == 0) return NULL;
TreeNode* root = new TreeNode(postorder[postorder.size() - 1]);
// 这里剪枝一下:如果后序数组为1,不需要进行分割
if (postorder.size() == 1) return root;
int delimiterIndex = 0;
while (delimiterIndex < inorder.size()) {
if (inorder[delimiterIndex] == root->val) break;
delimiterIndex++;
}
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end());
// 这里resize后续数组的长度
postorder.resize(postorder.size() - 1);
vector<int> leftPreorder(postorder.begin(), postorder.begin() + delimiterIndex);
vector<int> rightPreorder(postorder.begin() + delimiterIndex, postorder.end());
root->left = traversal(leftInorder, leftPreorder);
root->right = traversal(rightInorder, rightPreorder);
return root;
}
};